Handleiding Adaptieve Capaciteiten Test Algemene Intelligentie

Met ACT Algemene Intelligentie wordt een algemene intelligentiescore berekend – de zogenaamde g-score. Bekijk de handleiding.

PDF versie bekijken

De ACT Algemene Intelligentie is een intelligentietest die voor het werkveld van Human Resource Management (HRM) is ontwikkeld door Ixly. De ACT Algemene Intelligentie bevat drie subtests, namelijk Cijferreeksen, Figurenreeksen en Verbale Analogieën. Op basis van de scores op deze drie subtests wordt een algemene intelligentiescore berekend – de zogenaamde g-score. De ACT Algemene Intelligentie is primair ontwikkeld voor selectiedoeleinden, maar kan ook ingezet worden voor andere assessmentdoeleinden, zoals bij loopbaanvraagstukken waarbij een inschatting van het denkvermogen vereist of gewenst is.

Overzicht

De ACT Algemene Intelligentie is een intelligentietest die voor het werkveld van Human Resource Management (HRM) is ontwikkeld door Ixly[1]. De ACT Algemene Intelligentie is een adaptieve test die in een kort tijdsbestek een nauwkeurige meting geeft van het algemeen denkniveau van een persoon. De ACT Algemene Intelligentie bevat drie subtests, namelijk Cijferreeksen, Figurenreeksen en Verbale Analogieën. Aan de hand van deze tests kan respectievelijk cijfermatig analytisch vermogen, abstract-analytisch vermogen en verbaal analytisch vermogen bepaald worden. Op basis van de scores op deze drie subtests wordt een algemene intelligentiescore berekend – de zogenaamde g-score. De ACT Algemene Intelligentie is met name ontwikkeld voor selectiedoeleinden.

Deze handleiding volgt de structuur van het beoordelingssysteem van de Cotan (2009) voor de kwaliteit van tests:

1. Uitgangspunten van de testconstructie
2. Testmateriaal
3. Handleiding voor testgebruikers
4. Normen
5. Betrouwbaarheid
6. Begripsvaliditeit
7. Criteriumvaliditeit

 

[1] Ixly (voorheen Orga Toolkit B.V.) is een uitgeverij van online instrumenten en legt zich toe op het ontwikkelen, onderzoeken en beschikbaar stellen van vragenlijsten en tests voor de HRM beroepspraktijk. Deze worden via een internetapplicatie gedistribueerd.

Uitgangspunten bij de testconstructie

In dit hoofdstuk wordt een aantal theorieën over intelligentie besproken, en hoe intelligentie aan de hand van tests gemeten wordt. Het theoretisch uitgangspunt van de ACT Algemene Intelligentie wordt uiteengezet. Het komt erop neer dat ACT Algemene Intelligentie bestaat uit verschillende tests die allen een verschillend aspect van intelligentie meten, maar waarbij een overkoepelende algemene intelligentiefactor g verondersteld wordt. Ook de keuzes voor de gekozen subtests komen aan bod, evenals cultuurvrij testen.

Tevens wordt in dit hoofdstuk ingegaan op itemresponstheorie, het statistisch model dat gebruikt wordt bij adaptieve tests. Ook gaan we in op de voordelen van adaptief testen: het biedt een snelle en nauwkeurige manier van meten, waarbij minder sprake is van itembekendheid. Tot slot staan we stil bij de ontwikkelings- en ontstaansgeschiedenis van de ACT Algemene Intelligentie, en alle onderzoeken die daarvoor gedaan zijn. Hierbij wordt ook uitgebreid stil gestaan bij de gemaakte keuzes bij en onderzoeken naar de itempool, de methode van itemselectie, de startregel en de stopregel van de adaptieve test.

Testmateriaal

In dit hoofdstuk wordt ingegaan op de kenmerken van de items, zowel qua inhoud als qua psychometrische kenmerken van de itembanken. De ACT Algemene Intelligentie duurt maximaal ongeveer 45 minuten, maar de meeste kandidaten zullen er aanzienlijk minder tijd voor nodig hebben (20-30 minuten). Dit hoofdstuk bevat ook de instructies voor de testafname, informatie over eventueel onjuist gebruik van de software, het scoringssysteem en beveiliging van de test en het testmateriaal.

Handleiding voor testgebruikers

De ACT Algemene Intelligentie is ontwikkeld voor selectiedoeleinden maar kan in principe in elke situatie ingezet worden waarbij het van belang is meer te weten te komen over iemands intellectuele capaciteiten. In dit hoofdstuk worden de toepassingsmogelijkheden en ook de beperkingen van de test besproken en wordt ingegaan op de vereiste kennis voor het gebruik van de test. Tevens wordt er een instructie gegeven voor de testleider.

Er wordt verder ingegaan op de berekening van de g-score – de totaalscore op basis van de drie subtests – en de terugkoppeling van de scores in het rapport. Dit gebeurt aan de hand van een IQ-score, T-score, percentielscore en stenscore. In dit hoofdstuk wordt toegelicht – onder andere aan de hand van twee casussesn – hoe deze geïnterpreteerd dienen te worden. Tot slot worden er ingegaan op relevante informatie bij de interpretatie en wordt er informatie gegeven over de software en technische ondersteuning.

Normen

Bij de ACT Algemene Intelligentie gaat het om een normgerichte interpretatie. De normpopulaties zijn een representatie van personen met VMBO, MBO, HBO en WO opleidingsniveau in Nederland met betrekking tot de achtergrondvariabelen leeftijd en geslacht. Ten behoeve van de berekening van de IQ-scores is er ook een normgroep die wat betreft leeftijd en geslacht representatief is voor gehele beroepsbevolking van Nederland. De ACT Algemene Intelligentie is voor selectiesituaties genormeerd en dus gebaseerd op gegevens verkregen uit daadwerkelijke selectiesituaties uit de praktijk. Dit hoofdstuk beschrijft de samenstelling van de normgroep, de normeringsprocedure, de kenmerken van de scores in de normgroepen en geeft tevens informatie over de gebruikte  gestandaardiseerde scores. Ook wordt er ingegaan op het niet hanteren van speciale normgroepen op basis van bijvoorbeeld etniciteit. In Bijlagen 4.1. en 4.2. staan de normtabellen bij de test.

Betrouwbaarheid

In dit hoofdstuk worden de onderzoeken beschreven die gedaan zijn om de betrouwbaarheid van de ACT Algemene Intelligentie te bepalen. Hieruit bleek dat de betrouwbaarheid van de subtests voor relevante intelligentieniveaus acceptabel tot goed was, en van de g-score zeer goed (.92). De betrouwbaarheid van de subtests zijn ook relatief hoog (gemiddeld .81 dus >.80): voor Cijferreeksen (.81) en Verbale Analogieën (.86) zijn deze voldoende, terwijl de betrouwbaarheid van  Figurenreeksen (.77) net niet aan de drempelwaarde van .80 voldoet. We adviseren dan ook belangrijke beslissingen – zoals in selectiesituaties – voornamelijk te nemen op basis van de g-score.

Bovenstaande waarden zijn echter gebaseerd op de empirische betrouwbaarheid. Op basis van de SEM-methode zijn de betrouwbaarheid bij kandidaten hoog te noemen, namelijk .86, .83, .90 en .96 voor respectievelijk Cijferreeksen, Figurenreeksen, Verbale Analogieën en de g-score.

Er waren nauwelijks verschillen in de betrouwbaarheid van de metingen naar geslacht, leeftijd en etniciteit bij kandidaten die de ACT Algemene Intelligentie in selectiesituaties hadden gemaakt.

Begripsvaliditeit

Onderzoek naar de interne structuur toonde aan dat de relatief hoge relaties tussen de drie subtests verklaard konden worden door één factor – wat zoals verwacht duidt op de aanwezigheid van g. De onderlinge relaties bleven onveranderd wanneer we deze apart voor verschillende groepen berekenden (mannen/vrouwen, allochtonen/autochtonen, laag/midden/hoog opleidingsniveau, jong/middelbaar/oud). Verschillende onderzoeken toonden aan dat we kunnen aannemen dat de subtests van de ACT Algemene Intelligentie (voldoende) unidimensioneel zijn – dat wil zeggen dat de scores op deze subtests verklaard kunnen worden door één onderliggende verklarende factor. Dit is een belangrijke bevinding, omdat dit een belangrijke assumptie van itemresponstheorie is en overeenkomt met ons verkozen theoretisch model. Al deze resultaten bieden bewijs voor de solide structuur van de ACT Algemene Intelligentie.

Verder werden de hypotheses over verschillen tussen groepen op basis van achtergrondvariabelen (geslacht, leeftijd, opleiding en etniciteit) grotendeels bevestigd. Divergente validiteit werd aangetoond aan de hand van zwakke relaties tussen scores op de ACT Algemene Intelligentie en persoonlijkheid. Deze bevindingen geven aan dat scores op de ACT Algemene Intelligentie samen lijken te gaan met reële verschillen tussen groepen en dat het beoogde construct – intelligentie – inclusief deze reële verschillen tussen groepen, wordt gemeten.

Soortgenoten-validiteit werd aangetoond in een onderzoek met de MCT-H (Bleichrodt & Van den Berg, 1997, 2004), waarbij hoge correlaties gevonden werden tussen de subtests van de ACT Algemene Intelligentie en de MCT-H. De g-scores van de twee tests bleken zelfs nagenoeg identiek te zijn (r = .99). Ook werd een sterke onderlinge relatie aangetoond met een begrijpend lezen-test (r = .60). Convergente validiteit werd verder aangetoond aan de hand van een voorspelde positieve relatie met de persoonlijkheidstrek Openheid. Verder wordt een onderzoek beschreven waarin de voorspelde relatie tussen de ACT Algemene Intelligentie en reactiesnelheid wordt aangetoond.

Een onderzoek naar de aanwezigheid van afwijkende antwoordpatronen (person fit) toonde aan dat (1) weinig afwijkende responspatronen werden gevonden en (2) dat er nauwelijks tot geen verschillen waren tussen groepen (op basis van leeftijd, geslacht en etniciteit) in het aantal afwijkende antwoordpatronen. Omdat op basis van het antwoordpatroon iemands score wordt bepaald, ondersteunen deze bevindingen de validiteit van de verkregen testscores op individueel niveau.

Ter verdere ondersteuning van de validiteit van de verkregen testscores is ook onderzoek gedaan naar differential item functioning en differential test functioning (DTF): dit onderzoek toonde aan dat we op basis van leeftijd, geslacht en etniciteit weinig vertekeningen in itemresponses mogen verwachten bij de ACT Algemene Intelligentie. Dit is een belangrijke bevinding in relatie tot de fairness van de test: op basis van dit onderzoek kan geconcludeerd worden dat de test bij verschillende groepen ingezet kan worden.

Criteriumvaliditeit

In dit hoofdstuk worden tot slot twee onderzoeken beschreven die ondersteuning bieden voor de criteriumvaliditeit van de ACT Algemene Intelligentie. Bij criteriumvaliditeit gaat het erom of testscores een goede voorspeller zijn van gedrag of uitkomsten die buiten het domein van de test liggen.

In het eerste onderzoek (N = 92) werd aangetoond dat scores op de ACT Algemene Intelligentie sterk gerelateerd waren – in de orde van grote zoals we op basis van meta-analyses verwachtten – aan sociaaleconomische status van personen (inkomen, beroepsstatus, opleidingsniveau). Dit is belangrijk omdat de ACT Algemene Intelligentie ontwikkeld is voor het HR-werkveld waarin dit soort variabelen van belang zijn. Hieraan gerelateerd was een belangrijke bevinding dat ACT Algemene Intelligentie-scores samenhingen met werkcomplexiteit, en dat werkcomplexiteit de relatie tussen intelligentie en werktevredenheid medieerde. Tot slot werd aangetoond dat intelligentie gemeten door de ACT Intelligentie gerelateerd kon worden aan werkprestatie en dat deze relatie sterker was voor meer complexere banen. Intelligentie lijkt de belangrijkste prestatie voor werkprestatie (Schmidt & Hunter, 1998) en testgebruikers zullen sollicitanten selecteren op intelligentie omdat ze verwachten dat dit een voorspeller is van uiteindelijke prestaties op het werk. Dus, gezien het test- en meetdoel van de ACT Algemene Intelligentie, vormen de beschreven bevindingen belangrijke ondersteuning voor de criteriumvaliditeit van de ACT Algemene Intelligentie.

Een andere belangrijke bevinding uit het bovenstaande onderzoek was dat testscores een positieve relatie lieten zien met eindcijfers behaald op de middelbare school (r = .34). Voor veel van de personen in de steekproef waren deze cijfers jaren of zelfs decennia geleden behaald: de ACT Algemene Intelligentie bleek dus retrospectief een goede voorspeller voor schoolprestaties. Het tweede onderzoek (N = 66) bevestigde deze relatie met een concurrente studie naar de relatie tussen intelligentie, divergent denken en academische prestaties. Scores op de ACT Algemene Intelligentie waren positief gerelateerd aan scores op divergent denken-taken (r = .38) en het gemiddeld behaalde tentamencijfer (r = .37). Hoewel de ACT Algemene Intelligentie niet direct ontwikkeld is voor de voorspelling van academische prestaties, weten we uit de literatuur wel dat academische prestaties overeenkomsten vertonen met werkprestaties (Kuncel, Hezlett, & Ones, 2004) waardoor de gevonden resultaten ook van belang zijn voor de criteriumvaliditeit van de ACT Algemene Intelligentie.

 

 

1. Uitgangspunten van de testconstructie

In dit hoofdstuk wordt het begrip intelligentie nader toegelicht. Verschillende theorieën komen aan bod. Tevens wordt ingegaan op het meten van intelligentie middels intelligentietests. In het tweede deel van dit hoofdstuk wordt de ontwikkeling van de ACT Algemene Intelligentie en het gebruikte wiskundige model – itemresponstheorie – uitgebreid toegelicht.

1.1. Theorieën over intelligentie

In deze sectie worden de meest relevante theorieën besproken omtrent het begrip intelligentie. Alleen psychometrisch theorieën zullen hier besproken worden. Er zijn ook theorieën die intelligentie vanuit een andere hoek benaderen (bijvoorbeeld cognitieve psychologische theorieën en neurologisch-biologische theorieën). Deze focussen zich niet zozeer op het meten van intelligentie als wel op de beschrijving ervan. Omdat de ACT Algemene Intelligentie binnen de psychometrische traditie valt hebben we ervoor gekozen alleen deze te behandelen. Voor meer informatie over de theorieën met een andere invalshoek verwijzen we de geïnteresseerde lezer door naar bijvoorbeeld Gardner (2011).

Psychometrische theorieën vinden allemaal hun basis in de differentiële, ook wel psychometrische of correlationele school van psychologie. Het belangrijkste punt binnen deze visie op psychologie is de studie en het meten van individuele verschillen in psychologische karakteristieken (Walsh et al., 1990).

Galton’s General Mental Ability

De eerste die in wetenschappelijke zin aandacht besteedde aan het begrip intelligentie was Galton (1883) aan het eind van de 19^e eeuw. Hij formuleerde een theorie die sprak van general mental ability in mensen. Deze theorie is gebaseerd op het volgende idee: aangezien alle informatie ons via onze zintuigen bereikt, is intellect de som van alle simpele afzonderlijke aspecten van sensorisch functioneren. Volgens Galton ontstaat intelligentie dus uit de snelheid en precisie van onze sensorische responsen op omgevingsstimuli. Cattell (1890) ontwikkelde verschillende tests om deze afzonderlijke delen van het menselijke intellect te meten, zoals tests om het vermogen om verschillen in afmetingen, kleur en gewicht te bepalen. Hij noemden deze tests mental tests. De tests bleken onderling nauwelijks te correleren en leken om deze reden dus niet een overkoepelende general mental ability te meten. Verder waren de vele verschillende tests die nodig waren om het construct te meten en de vele herhaalde afnamen die nodig waren om een betrouwbare score te krijgen nogal onpraktisch. Aan het begin van de 21^e eeuw is deze kijk op intelligentie dan ook verlaten (Walsh et al., 1990; Janda, 1998).

Binet-Simon

Tegelijk met Galton en Cattell ontwikkelden Alfred Binet en Theophile Simon een duidelijke andere theorie met betrekking tot menselijke intelligentie. Zij deden dit met als doel een test te ontwikkelen die geestelijke gehandicapte kinderen zou kunnen onderscheiden van normaal ontwikkelende kinderen. Binet en Simon waren van mening dat onder intelligentie de “hogere mentale processen” (zoals oordelen en redeneren) vielen. Ook stelden zij dat de capaciteit om deze hogere mentale processen uit te voeren zou moeten toenemen met de leeftijd van een kind. De score op de Binet-Simon test werd gegeven als het mentale niveau of de mentale leeftijd van een kind. Deze test kreeg veel aandacht en werd in 1916 bewerkt door Lewis Terman en later door enkele anderen, tot de test die nu bekend staat als de Stanford – Binet test aan de hand waarvan de “Intelligentie Quotiënt” oftewel het IQ bepaald wordt.

Spearman’s Twee Factoren Theorie van Intelligentie

Charles Spearman (1923) onderzocht met zijn zelf ontwikkelde techniek van Factor Analyse de tests van Galton en Cattell. Hij concludeerde, in tegenstelling tot anderen, dat veel van deze tests wel onderling positief correleerden. Hij trok hieruit de conclusie dat een general mental ability, zoals Galton deze had gedefinieerd, wel degelijk bestond en noemde dit general intelligence oftewel g – een conclusie die vandaag de dag nog steeds heerst. Hij stelde verder dat testscores veroorzaakt werden door twee componenten: de g-factor en factoren specifiek voor de betreffende test, die hij “s” noemde. Deze theorie staat bekend als Spearman’s Twee Factoren Theorie van Intelligentie (Spearman, 1923). Intelligentie als zijnde g kan als volgt gedefinieerd worden:

“intelligentie is niet wat we weten op een bepaald moment, maar hoe goed we kunnen redeneren, problemen oplossen, abstract denken, en informatie flexibel en efficiënt manipuleren, met name wanneer het stimulusmateriaal in bepaalde mate nieuw is” (Walsh et al., 1990).

Thurstone’s Primary Mental Abilities

Spearman’s theorie werd niet algemeen geaccepteerd door zijn tijdsgenoten. Een voorbeeld van een tegenstander van de twee- factor-theorie was Leon Thurstone (1938). Thurstone stelde dat de overlap tussen verschillende intelligentietests niet veroorzaakt werd door de g-factor, maar door het feit dat bij het oplossen van bepaalde test dezelfde vaardigheden nodig waren. Thurstone meende dat intellectueel functioneren het best beschreven kon worden als een verzameling onafhankelijke vaardigheden. Middels multiple factor analyse formuleerde hij dertien van deze primary mental abilities. Om deze mogelijkheden te testen ontwikkelde hij een batterij tests, genaamd de Primary Mental Abilities Test (PMA). De theorie van Thurstone is, samen met bijvoorbeeld die van Guilford (1964, 1967), een voorbeeld van een Multiple Factor Theorie van Intelligentie. Guilford (1977) stelde dat menselijke capaciteiten het best beschreven konden worden door de combinatie van drie dimensies: vijf mentale ‘operaties’ (cognitie, geheugen, divergente productie, convergente productie en evaluatie), vijf soorten inhoud (visueel, auditief, symbolisch, semantisch en gedragsmatig) en zes producten (eenheden, klassen, relaties, systemen, transformaties en implicaties). Omdat Guilford veronderstelde dat deze drie dimensies onafhankelijk van elkaar waren, resulteert dit in (5x5x6) 150 theoretisch onafhankelijke intelligentiecomponenten. Guilford (1982) moest echter concluderen dat deze onafhankelijkheid empirisch niet stand hield: de verschillende specifieke capaciteiten bleken positief met elkaar samen te hangen.

Multiple factor versus hiërarchische modellen

Kenmerkend van de multiple factor theorieën is dat zij ervan uitgaan dat alle factoren gelijk zijn wat betreft belangrijkheid en generaliteit. Andere onderzoekers waren echter van mening dat er wel degelijk een hiërarchie in de factoren was aan te tonen middels factor analyse – een hiërarchisch model met zowel een algemene factor als specifieke factoren. Zij stelden dus feitelijk een combinatie van het model van Spearman en Thurstone voor. Deze kijk op de analyse van scores op mentale tests resulteerde in de Hierarchical models of the nature of mental abilities. Voorbeelden van onderzoekers die dergelijke modellen ontwikkelden zijn Vernon (1960) en Burt (1949).

Fluid en crystallized intelligentie

Een ander voorbeeld van een hiërarchisch model – waarschijnlijk één van de meest bekende – is het model van Cattell (1941, 1963, 1971), later uitgewerkt samen met Horn (Horn & Cattell, 1966, 1967). Het model van Cattell en Horn deelt g op in fluid intelligence en crystallized intelligence, een indeling die inmiddels algemeen geaccepteerd is (Kline, 1992). Omdat de factoren fluid en crystallized intelligentie zich tussen g en scores op specifieke tests (bijvoorbeeld ‘verbaal begrip’) in bevinden is hier sprake van een hiërarchisch model. Crystallized intelligentie betreft het toepassen van aangeleerde vaardigheden, kennis en ervaringen. Hierdoor speelt cultuur en opleiding bij crystallized intelligentie ook een rol. Alhoewel het niet hetzelfde is als geheugen, is gebruik van langetermijngeheugen wel een belangrijke component. Tests die crystallized intelligentie meten, geven vooral weer wat iemand al geleerd heeft: tests die iemands kennis over geografie en geschiedenis of iemands vocabulaire meten, meten crystallized intelligentie. Aan de andere kant meet Fluid intelligentie iemands vermogen om logisch te redeneren en (nieuwe) problemen op te lossen in nieuwe situaties, los van eerder verkregen kennis: om deze reden wordt fluid intelligentie meer beschouwd als een fundamenteel karakteristiek van een persoon, met een genetische basis. Om deze reden wordt g meer geassocieerd met fluid intelligentie dan crystallized intelligentie.

Conclusie

Zoals hiervoor beschreven zijn er vele verschillende theorieën omtrent intelligentie. Tot op heden is er nog geen volledige consensus over wat er nu precies onder intelligentie verstaan moet worden en welke van de psychometrische theorieën de beste beschrijving van de werkelijkheid is. In een samenvatting van de psychometrische theorieën van intelligentie concludeert Kline (1992) dat een tussenweg tussen de hiërarchische- en multipele factor theorieën als meest realistisch beschouwd kan worden. Het bestaan van g, oftewel een algemene intelligentie factor, kan worden afgeleid uit het feit dat scores op verschillende subtests waaruit intelligentietests bestaan een redelijke mate van samenhang laten zien. Echter, de hoogte van deze samenhang sluit het bestaan van meer specifieke factoren niet uit. Deze conclusie van Kline (1992) vormt dan ook de basis van de ACT Algemene Intelligentie.

1.2. Intelligentietests

Zoals in de vorige sectie beschreven, zijn er in de loop der tijd zeer veel verschillende typen intelligentietests ontwikkeld; van de sensorische tests van Cattell tot de vandaag de dag nog steeds gebruikte (sterk gereviseerde vierde editie van) Stanford-Binet (Thorndike et al., 1986).

Intelligentietests kunnen op een aantal manieren geclassificeerd worden.

Classificering op afname

Eén van deze classificatiesystemen is die in individueel afgenomen tests en groepsgewijs afgenomen tests (Walsh et al., 1990). De individueel afgenomen tests worden door een speciaal getraind persoon afgenomen bij één individu. Deze tests bevatten onderdelen waarbij gewerkt wordt met allerlei materialen of waarbij de tijd opgenomen dient te worden. De prestatie van de kandidaat moet geobserveerd worden om gescoord te kunnen worden. De Stanford–Binet is een voorbeeld van een test die individueel afgenomen dient te worden.

Bij groepsgewijs afgenomen tests kunnen grote groepen mensen tegelijk dezelfde test afleggen. Voordeel boven de individueel afgenomen test is uiteraard de kosteneffectiviteit. Tevens is hier sprake van meer standaardisatie van de afname dan bij de individueel afgenomen tests. Nadeel is dat er bij een degelijke testafname minder rekening kan worden gehouden met specifieke individuele factoren en er dus een minder uitgebreide beschrijving van de persoon verkregen wordt. Een bekend voorbeeld van een groepsgewijs afgenomen test is de Army Alpha die ontwikkeld werd door Yerkes en collega’s en in 1917 geïntroduceerd werd om de grote aantallen rekruten voor de Eerste Wereldoorlog snel te kunnen beoordelen op hun capaciteiten. De ACT Algemene Intelligentie is een test die onder de groepsgewijs afgenomen tests gecategoriseerd kan worden, aangezien deze volledig gestandaardiseerd is en met de computer afgenomen wordt. In de praktijk zullen kandidaten de tests echter vaak individueel voltooien, als onderdeel van een selectieprocedure.

Classificering op inhoud

Naast een onderscheid in wijze van afname en scoring van tests, kan er ook een onderscheid in tests gemaakt worden op basis van de verschillende typen inhoud van de test. Zo kan er een onderscheid gemaakt worden in verbale tests (taal; gesproken of geschreven), non-verbale tests (figuren, symbolen) en prestatietests (puzzels, doolhoven). Er bestaan tests die slechts uit één itemtype: een bekend voorbeeld hiervan is de Raven Progressive Matrices (Raven, 1936; Raven, Raven, & Court, 2003). In lijn met g-theorie is het echter gebruikelijker voor tests, om verschillende tests met verschillende itemtypes (dus resulterend in verschillende ‘schalen’) te combineren tot een testbatterij. Deze testbatterijen combineren vaak tests met verbale items en non-verbale items. Bekende voorbeelden hiervan zijn de internationale Wechsler Intelligence Scale for Children (WISC; Wechsler et al., 2003) en de Wechsler Adult Intelligence Scale (WAIS; Wechsler, 2008), en de Drenth Testtheorie Hoger Niveau (DTHN; Drenth, Van Wieringen & Hoolwerf, 2001) in Nederland. De ACT Algemene Intelligentie kan ook onder deze testcategorie geschaard worden.

Classificering op culturele specificiteit

Tot slot kan er nog een onderscheid gemaakt worden in culturele-specificiteit-van-de-testinhoud. Cultuur-geladen tests zijn tests die de nadruk leggen op kennis en vaardigheden zoals die worden aangeleerd in het onderwijs systeem van een bepaalde cultuur. Cultuurvrije items zijn non-verbale items en prestaties die niet specifiek zijn voor een specifieke cultuur of op school worden aangeleerd (Walsh et al., 1990). Bij de ACT Algemene Intelligentie is getracht de items zoveel mogelijk cultuurvrij te maken. Ongeacht het test- of itemtype is de veronderstelling dat scores hierop een manifestatie zijn van het algemeen denkvermogen en dus ‘laden’ op g – dit geldt dus ook voor de ACT Algemene Intelligentie.

1.3. Theoretisch uitgangspunt ACT Algemene Intelligentie

1.3.1. Meetdoel

De ACT Algemene Intelligentie is ontwikkeld voor selectiedoeleinden: het moet een instrument zijn om inzicht te krijgen in de intellectuele capaciteiten van een kandidaat, om zo een goede, geïnformeerde keuze te maken bij het selectievraagstuk. Een belangrijke rechtvaardiging hierbij is het feit dat g de belangrijkste voorspeller is gebleken voor werkprestaties (Schmidt & Hunter, 1998) – belangrijker dan andere variabelen waarop mensen kunnen verschillen, zoals persoonlijkheid (Schmidt & Hunter, 1998). Een nevendoel is dat verschillen tussen personen – bijvoorbeeld tussen allochtonen en allochtonen – zo min mogelijk de meting mogen beïnvloeden omdat deze ook de uitkomst zullen beïnvloeden.

Hoewel de ACT Algemene Intelligentie primair ontwikkeld is voor selectiedoeleinden, kan deze ook ingezet worden voor andere assessmentdoeleinden, zoals bij loopbaanvraagstukken waarbij een inschatting van het denkvermogen vereist of gewenst is.

1.3.2. Keuze van theoretisch model voor de ACT Algemene Intelligentie

De conclusie van Kline (1992) vormt de basis van de ACT Algemene Intelligentie: er wordt een g-factor verondersteld, oftewel een algemene intelligentie factor, afgeleid uit het feit dat scores op verschillende subtests samenhang laten zien, waarbij de hoogte van deze samenhang het bestaan van meer specifieke factoren niet uitsluit.

Hoewel er dus enige overeenstemming is over het bestaan van g, is er tot op de dag van vandaag discussie over hoe scores op intelligentietests statistisch het best gemodelleerd kunnen worden (zie Jensen en Weng, 1994 en Gignac, 2016), waarbij de modellen uit sectie 1.1. nog steeds de uitgangspunten vormen. Jensen en Weng (1994) toonden aan dat, hoewel er veel verschillende modellen mogelijk zijn, g voor een breed scala aan uitkomsten in principe een betere voorspeller is dan de scores op de afzonderlijke tests. Met andere woorden, hoe je g ook modelleert: “Almost any g is a “good” g and is certainly better than no g.” (Jensen en Weng, 1994, p. 231). Dit is een belangrijke reden waarom het uitgangspunt bij de ACT Algemene Intelligentie de g-factor is.

Naast het ontbreken van een volledige consensus omtrent het te hanteren model, bestaat er ook geen volledige overeenstemming omtrent de exacte betekenis of interpretatie van g. Benamingen als “mentale energie”, “gegeneraliseerd abstract redenatievermogen” en “enkel statistische grootheid” worden hiervoor gebruikt (Janda, 1998). Voorzichtig kan wel gesteld worden dat zowel Binet’s nadruk op het vermogen te oordelen en redeneren, als ook Spearman’s principe van het leren van relaties en correlaties, de basis vormen van onze huidige conceptie van intelligentie. Wij onderschrijven dus de definitie van Walsh et al. (1990), zoals vermeld op pagina 5 en 6.

Concluderend kunnen we stellen dat het model van de ACT Algemene Intelligentie van Ixly is gebaseerd op het meetdoel (en de resultaten van Schmidt en Hunter omtrent dit doel), de getrokken conclusies door Kline (1992) en de bovenstaande definitie van Walsh et al. (1990). Dit houdt in dat het door Ixly gehanteerde model bestaat uit verschillende tests, die allen een verschillend aspect van intelligentie meten, maar waarbij een overkoepelende algemene intelligentiefactor g verondersteld wordt. Het uitgangspunt bij de ontwikkeling van de capaciteitentests van Ixly is om deze met name van toepassing te laten zijn op de werksituatie. Aangezien binnen verschillende functies verschillende capaciteiten van belang zullen zijn, zal het in de praktijk wenselijk zijn om door middel van subtests inzicht te krijgen in specifieke capaciteiten die voor de desbetreffende functie van belang zijn. Een specifiek, op dat moment relevant, onderdeel van intelligentie wordt hiermee in kaart gebracht. Zo is het bijvoorbeeld bij een financiële functie van belang de cijfermatige capaciteiten van een persoon in kaart te brengen. Verbale capaciteiten zijn voor een dergelijke functie minder van belang, terwijl er andere functies zullen zijn waar verbale capaciteiten een grotere rol zullen spelen. Hoewel deze specifieke inzichten belangrijk zijn, gaat het in de praktijk echter vaak om iemands algemene denkvermogen, ook omdat dit de belangrijkste voorspeller voor werkprestatie is (Schmidt & Hunter, 1992, 1998, 2004). Kortom, hoewel de scores op de specifieke tests kwalitatief inzicht geven in het algemeen denkvermogen, dienen selectiebeslissingen voornamelijk op basis van de g-score (algemene intelligentie) genomen te worden. De scores op de specifieke aspecten van intelligentie zullen samenhangen, omdat ze voortvloeien uit de algemene intelligentie (g) van een persoon. Daarom zegt een score gebaseerd op de specifiekere aspecten van intelligentie iets over de algemene intelligentie van een persoon.

1.3.3. Cultuurvrij testen

Achtergrond

De afgelopen decennia is er in Nederland veel nadruk komen te liggen op mogelijke partijdigheid (ook wel ‘testbias’ of ‘itembias’ genoemd) van (psychologische) tests voor etnische minderheden (allochtonen versus autochtonen). Er is sprake van partijdigheid wanneer testscores verschillende betekenissen hebben voor bepaalde groepen. Er is ook sprake van partijdigheid wanneer de relatie tussen de testscore en een criterium – zoals de relatie tussen intelligentie en werkprestatie – verschilt voor bepaalde groepen (‘differentiële predictie’; Van den Berg & Bleichrodt, 2000). Partijdigheid kan door verschillende oorzaken optreden, bijvoorbeeld door verschillen tussen groepen in taalvaardigheid, bekendheid met de manier van testen of bekendheid met bepaalde (culturele) begrippen. Twee personen die niet van elkaar verschillen wat betreft intelligentie zouden andere testscores kunnen behalen, doordat bijvoorbeeld de ene persoon dyslectisch is en de ander niet.

Het moge duidelijk zijn dat partijdigheid een probleem vormt, omdat testscores hierdoor niet te vergelijken zijn. Bepaalde groepen kunnen benadeeld worden als belangrijke beslissingen (zoals in selectiesituaties) op basis van deze scores genomen worden.

Instrumenten worden in eerste instantie ontworpen door en voor leden uit een bepaalde cultuur of samenleving. Wanneer deze vervolgens gebruikt worden bij een groep uit een andere cultuur kan culturele vertekening optreden (Bochhah, Kort & Seddik, 2005). Mogelijke taalproblemen of -achterstanden kunnen deze vertekening vergroten (Bleichrodt & Van den Berg, 2000). Daarom is het belangrijk te waarborgen dat testscores van allochtonen en autochtonen met elkaar te vergelijken zijn en geen culturele vertekeningen laten zien. Hierover verscheen in 1990 het rapport Toepasbaarheid van psychologische tests bij allochtonen (Hofstee et al., 1990), waarin geconcludeerd werd dat een groot aantal tests minder of niet goed bruikbaar waren bij allochtonen, omdat er sprake was van te grote verschillen in scores tussen allochtonen en autochtonen en/of verschillende constructen gemeten leken te worden bij de twee groepen. Bij veel tests ontbrak echter informatie over eventuele testbias; in het rapport werd dan ook geadviseerd om meer onderzoek te rapporteren naar eventuele testbias bij etnische minderheden. Tien jaar later verschenen er nieuwe rapporten (Bleichrodt & Van de Vijver, 2001; Van de Vijver, Bochhah, Kort & Seddik, 2001) waarin geconcludeerd werd dat – enige uitzonderingen daargelaten (bijvoorbeeld de MCT-tests; Bleichrodt & Van den Berg, 1997, 2004) – de situatie niet verbeterd was. In 2005 werden de meest gebruikte tests in de selectiepraktijk beoordeeld op partijdigheid, waarbij er nog steeds belangrijke verschillen op dit gebied tussen tests bleken te zijn (Bochhah, Kort & Seddik, 2005). Vanaf 2011 heeft een werkgroep van het Nederlands Instituut van Psychologen (NIP) en de Cotan nog meer de nadruk gelegd op fairness (vrij zijn van testbias) bij de beoordeling van psychologische tests, wat in 2015 heeft geresulteerd in een fairness matrijs bij nieuwe testbeoordelingen.

Implementatie

In navolging van het bovenstaande, vinden wij het belangrijk dat persoonlijke kenmerken die niet van belang zijn voor de te meten eigenschap (intelligentie) geen invloed hebben op de testresultaten of op de interpretatie daarvan. Bij de ontwikkeling van de ACT Algemene Intelligentie is daarom zoveel mogelijk getracht de test cultuurvrij te houden. Dit uitgangspunt heeft onder andere invloed gehad op de keuze van de subtests, de itemontwikkeling en het taalgebruik (bijvoorbeeld in de instructies).

In het taalgebruik is getracht zoveel mogelijk simpele woorden te gebruiken. Meer informatie hierover is ook te vinden in Hoofdstuk 2. Bij het formuleren van de items voor Verbale Analogieën hebben we geprobeerd zo min mogelijk moeilijke woorden te gebruiken (meer hierover in de sectie Verbale Analogieën), en geprobeerd het gebruik van racistische, seksistische, etnocentrische en androcentrische uitdrukkingen te vermijden (Hofstee, 1991).

De keuze van de subtests in relatie tot cultuurvrij testen wordt in de volgende sectie besproken.

Keuze van subtests

Bij de keuze van de subtests voor de algemene intelligentie vormden cultuurvrij testen en het theoretisch uitgangspunt (zie sectie 1.3.2.) de belangrijkste twee uitgangspunten. Daarom is gekozen voor subtests die in eerder onderzoek (zie volgende secties) een lage culturele bias en een hoge lading op de g-factor vertoonden (waarbij dus met name fluid intelligentie gemeten dient te worden in tegenstelling tot crystallized intelligentie).

Momenteel zijn er drie adaptieve subtests ontwikkeld die samen de ACT Algemene Intelligentie vormen: de Cijferreeksen-, Figurenreeksen- en de Verbale Analogieëntest. Aan de hand van deze tests kan respectievelijk cijfermatig analytisch vermogen, abstract-analytisch vermogen en verbaal analytisch vermogen bepaald worden. Samen vormen deze subtests een score op de g-factor, wat aangeduid kan worden als algemene mentale intelligentie.

Algemeen kunnen we stellen dat de keuze voor deze drie subtests voortbouwt op de zeer oude (en zichzelf herhaaldelijk bewezen) traditie van intelligentiemetingen. Er bestaan ontzettend veel testbatterijen die intelligentie meten, en het is bekend dat in vrijwel alle testbatterijen het onderscheid gemaakt kan worden in de domeinen verbaal, numeriek en abstract/figuratief (zie bijvoorbeeld het radex-model van Guttman, 1954, 1969). In wetenschappelijk onderzoek wordt dit onderscheid ook vaak gehanteerd (zie bijvoorbeeld Ackerman, Beier, & Boyle, 2002). Meer specifiek bevat de meerderheid van de tests subtests die lijken op de Cijferreeksen, Figurenreeksen en Verbale Analogieën van de ACT Algemene Intelligentie (Drenth, Van Wieringen & Hoolwerf, 2001; Wechsler, 2008). Veel korte versie (‘short forms’) van uitgebreidere testbatterijen bevatten bijvoorbeeld (één van) deze tests (Pierson, Kilmer, Rothlisberg, & McIntosh, 2012; Sattler, 2001, 2008). Het zijn dus vrij ‘traditionele’ intelligentietests. De specifieke onderbouwingen voor de keuzes van de subtests wat betreft cultuurvrij testen en het theoretisch uitgangspunt van de ACT Algemene Intelligentie worden hieronder toegelicht.

1.3.3.1. Cijferreeksen 

Het concept van de Cijferreeksentest is al zeer oud (Thurstone, 1938). Bij de Cijferreeksentest wordt de kandidaat geacht een logisch patroon te herkennen in de getoonde reeks cijfers: omdat het hier gaat om het herkennen van patronen, logisch redeneren en het oplossen van nieuwe, onbekende problemen meten cijferreeksentests vooral fluid intelligentie. Er zal echter ook wat van het rekenvermogen gevraagd worden van de kandidaat, dus voor een deel zal de test ook crystallized intelligentie meten. Echter, intelligentietests zullen vrijwel altijd mengvormen van beiden zijn (zie bijvoorbeeld Kaufman & Horn, 1996).

De items zijn non-verbaal: dit zorgt ervoor dat de subtest ook goed in te zetten is bij kandidaten met een taalachterstand, Nederlands als tweede taal of dyslexie. Omdat de test fluid intelligentie meet is de test redelijk cultuurvrij. Doordat het rekenvermogen echter beïnvloed kan worden door opleiding (wat weer samen kan hangen met culturele achtergrond), zal deze subtest minder cultuurvrij zijn dan bijvoorbeeld de Figurenreeksen (zie volgende sectie). Onderzoek met de Multiculturele Capaciteiten Test (MCT-M, Bleichrodt & Van den Berg, 1997, 2004) liet echter zien dat er geen significante verschillen waren tussen autochtonen en tweedegeneratie allochtonen op de cijferreeksentest (Van den Berg & Bleichrodt, 2000), al moet hier wel bij vermeld worden dat de MCT specifiek ontworpen was om culturele verschillen in testscores tegen te gaan.

1.3.3.2. Figurenreeksen

 Bij de Figurenreeksen wordt de kandidaat gevraagd om in een reeks figuren een patroon te ontdekken en deze op logische wijze toe te passen. Dit testtype wordt ook wel matrixtest genoemd, en is in de jaren dertig van de vorige eeuw ontwikkeld (Raven, Raven & Court, 2003). Matrixtests worden verondersteld general mental ability (g) te meten, getuige hun hoge lading op de g-factor (Spearman, 1946).

Figurenreeksen is een test die fluid intelligentie meet. Fluid intelligentietests worden beschouwd als meer cultuurvrij dan crystallized intelligentietests, maar dit type test wordt over het algemeen gezien als geheel cultuurvrij test, omdat er gebruik gemaakt wordt van abstracte figuren en de verbale instructie tot een minimum beperkt kan blijven (Bleichrodt & van de Vijver, 2000). Het Nederlands Instituut voor Psychologen (NIP) heeft dan ook geconcludeerd dat dit type test goed inzetbaar en bruikbaar is om af te nemen bij etnische minderheidsgroepen (Bochhah, Kort & Seddik, 2005). Deze tests wordt dan ook veel gebruikt in cross-cultureel onderzoek en wordt vaak toegepast bij allochtone kandidaten.

 Alhoewel de Figurenreeksen-items op een aantal kenmerken onderling van elkaar verschillen, komen ze overeen op een aantal belangrijke aspecten. Ten eerste zijn alle items, net als bij de Cijferreeksen, non-verbaal. Dit zorgt ervoor dat de test ook goed in te zetten is bij kandidaten met een taalachterstand, Nederlands als tweede taal of dyslexie. Ten tweede is de test zoals vermeld cultuurvrij. Zo is er in de opgaven gebruik gemaakt van cultuuronafhankelijke tekens en afbeeldingen. Dit houdt in dat er voor de beantwoording van de items geen kennis van de wereld of de maatschappij vereist is. Hierdoor is de test inzetbaar bij kandidaten van verschillende culturen en achtergronden. Tot slot is de inhoud van de items niet iets dat op school geleerd wordt: dit is het grootste verschil met de Cijferreeksen subtest. Bij Cijferreeksen zit namelijk altijd een rekencomponent. Dit is bij de Figurenreeksentest niet het geval. Dit alles zorgt ervoor dat de Figurenreeksen subtest een eerlijke en cultuurvrije test is, waarvan de resultaten minder vertekend zullen worden door achtergrondvariabelen.

1.3.3.3. Verbale Analogieën

 De Verbale Analogieëntest, zoals de naam al aanduidt, kent een verbale component. Over het algemeen laten tests waar een beroep wordt gedaan op het verbale vermogen grotere culturele verschillen zien dan non-verbale tests (Van den Berg & Bleichrodt, 2000), bijwijlen van alarmerende grootte (soms wel tussen de 1 tot 2 standaarddeviaties; Evers & Te Nijenhuis, 1999; Resing, Bleichrodt & Drenth, 1986).

Gezien de verbale component zou men snel de conclusie kunnen trekken dat deze test crystallized intelligentie meet. Echter, dit is niet per definitie waar: verbale tests (bijvoorbeeld analogieën) kunnen zo ontworpen worden dat ze wel degelijk laden op fluid intelligentie. Dit is het geval als de gebruikte woorden makkelijk en bij iedereen bekend verondersteld mogen worden (Cattell, 1987; Horn, 1965). Het gaat dan namelijk om het zien van complexere relaties en patronen tussen fundamentele elementen, waar nauwelijks tot geen eerdere kennis vereist is. Verbale Analogieëntests waarbij eenvoudige, bekende woorden gebruikt worden kunnen dan ook beschouwd worden als een goede indicatie van g (Holyoak & Morrison, 2013; Spearman, 1946). Deze staan in contrast met tests die echt verbaal vermogen meten, bijvoorbeeld waarbij in een zin de juiste vervoeging van een werkwoord ingevuld moet worden: dit kunnen we echt zien als een test van crystallized intelligentie.

Bij het ontwikkelen van de items van de Verbale Analogieëntest hebben we om bovenstaande redenen zoveel mogelijk geprobeerd bekende, makkelijke woorden te gebruiken. De complexiteit van een item moet komen uit de complexiteit van de relaties, en niet van de gebruikte woorden. Toch zullen er altijd verschillen zijn in taalkennis en woordenschat die van invloed kunnen zijn op de resultaten. Daarom kunnen we verwachten dat deze subtest de meeste crystallized intelligentie zal oppikken van alle drie de subtests. Zo heeft onderzoek aangetoond dat verbale analogieëntests niet cultuurvrij zijn: allochtonen scoren vaak lager dan autochtonen op verbale analogieëntests (zie bijvoorbeeld Van den Berg & Bleichrodt, 2000). De verschillen zijn echter klein (Meulders & Vandenberk, 2005). Empirisch onderzoek met de ACT Algemene Intelligentie heeft dan ook aangetoond dat de verschillen bij deze test – in vergelijking met andere tests – relatief klein zijn (zie Hoofdstuk 6).

 Conclusie over keuze subtests

Binnen de ACT Algemene Intelligentie is de Figurenreeksen van deze drie tests het meest cultuurvrij omdat er geen beroep wordt gedaan op het verbale vermogen van de kandidaat. Bij het afnemen van deze tests kan dit cultuurelement in overweging genomen worden. Het indelen van de drie tests in verbaal/non-verbaal kan als volgt gedaan worden: de tests Figurenreeksen en Cijferreeksen kunnen benoemd worden als non-verbale tests, terwijl de test Verbale Analogieën een duidelijk verbale test is.

1.4. Adaptieve Capaciteiten Test (ACT) Algemene Intelligentie

 De ACT Algemene Intelligentie heeft expliciet als doel om zoveel mogelijk cultuurvrij te testen, wat bij veel – voornamelijk oudere tests – niet specifiek het geval was. Een groot voordeel van de ACT Algemene Intelligentie is verder dat het een adaptieve test is. De voordelen hiervan worden in de rest van dit hoofdstuk verder uiteengezet, maar we willen hier vast benadrukken dat een belangrijk resultaat hiervan de zeer beperkte afnametijd is. Met ongeveer 30 tot 40 minuten is de ACT Algemene Intelligentie, zeker vergeleken met andere tests, een test die in zeer korte tijd een nauwkeurige schatting van het intelligentieniveau van een persoon kan geven.

Adaptief testen

 De ACT Algemene Intelligentie meet de intelligentie van een persoon op adaptieve wijze: bij een adaptieve test krijgt de kandidaat steeds het beste (= het meest informatieve) item dat geselecteerd is op zijn/haar niveau, op basis van zijn/haar eerder gegeven antwoorden.

Specifiek gaat dit als volgt: de kandidaat krijgt eerst een vraag op ongeveer gemiddeld niveau. Op basis van het gegeven antwoord wordt iemands niveau (vanaf nu theta (θ) genoemd) bepaald. Op basis van vooraf gestelde criteria wordt een nieuw item uit de grote itembank gezocht die voor dit niveau het meest informatief is. Op basis van dit gegeven antwoord wordt weer de nieuwe θ bepaald, waarna weer het beste item wordt gezocht, et cetera. Zodra θ nauwkeurig genoeg gemeten is, als het zogenoemde stopcriterium bereikt is, stopt de test.

1.4.1. Voordelen adaptief testen

Adaptief testen heeft een aantal voordelen ten opzichte van klassieke, lineaire tests.

Testen op het juiste niveau

 De kandidaat wordt altijd getest op zijn/haar eigen niveau, op basis van eerder gegeven antwoorden. Hiermee vermijden we dat kandidaten met een laag niveau te moeilijke vragen krijgen, en dat kandidaten met een hoog niveau te makkelijke vragen krijgen. Er wordt aangenomen dat dit leidt tot een verhoogde motivatie bij het maken van de test ten opzichte van klassieke, niet adaptieve tests (Linacre, 2000; Mead & Drasgow, 1993; Sands & Waters, 1997; Wainer, 1997; Weiss & Betz, 1973). Mensen met een lager niveau raken minder gedemotiveerd of afgeschrikt door te moeilijke items, terwijl mensen met een hoger niveau niet verveeld worden of onoplettend door te makkelijke items gaan (Wise, 2014). Echter, andere onderzoeken lijken te suggereren dat adaptief testen gepaard kan gaan met demotivatie bij testnemers, bijvoorbeeld omdat ze tussendoor geen makkelijkere items krijgen (om weer even ‘op adem te komen’/bevestigd te worden in hun kunnen) en geen vragen kunnen overslaan (Frey, Hartig, Moosbrugger, 2009; Hausler & Sommer, 2008; Ortner, Weisskopf, & Koch, 2013; Tonidandel, Quiñones, & Adams, 2002). Dit laatste punt is echter niet uniek voor adaptieve tests. Ook het feit dat bij een adaptieve test (relatief) sneller moeilijkere items gesteld worden wat leidt een percentage correct van ongeveer 50% zou kunnen leiden tot motivatie (Colwell, 2013). Of het adaptieve karakter van de test wordt uitgelegd in de instructies heeft echter een belangrijke positieve invloed op de motivatie in en prestaties op adaptieve tests (Wise, 2014). Daarom is gekozen de adaptieve procedure (weliswaar op simpele wijze) uit te leggen in de instructies van de ACT Algemene Intelligentie (zie Hoofdstuk 2).

Hoewel het adaptieve karakter van een test tot meer motivatie lijkt te leiden, is hier dus nog geen complete consensus over in de literatuur. Adaptief testen kent echter nog meer voordelen die hieronder besproken worden.

Korter testen

 Door het gebruik van een adaptieve test zijn we in staat om in veel kortere tijd een zeer betrouwbare meting van de vermogens van de kandidaat te bereiken, omdat er geen ‘nutteloze’ items bevraagd worden (Hambleton, Swaminathan, & Rogers, 1991; Weiss & Kingsbury, 1984). Dit werkt kostenbesparend in het geval de kandidaat op locatie de test maakt. Ook vragen we op deze manier minder tijd van de kandidaat.

 Nauwkeuriger meten

Omdat we geen items gebruiken die geen informatie geven over de vermogens van de kandidaat, bijvoorbeeld omdat ze veel te makkelijk of veel te moeilijk zijn, wordt er nauwkeuriger gemeten (Hambleton et al., 1991; Weiss & Kingsbury, 1984).

Geringere bekendheid van de items

Veel capaciteitentests kennen het probleem van itembekendheid, bijvoorbeeld op internet (Sympson & Hetter, 1985; Van der Linden & Glas, 2010; Veldkamp, 2010). U kunt zich voorstellen dat de betrouwbaarheid van de uitslag van een test hierdoor drastisch afneemt. Onze adaptieve intelligentietest kent dit probleem niet. De itembank voor elke subtest bestaat uit een groot aantal vragen (>100 per subtest), waarvan iedere kandidaat er slechts een klein aantal te zien krijgt. Bovendien worden de items niet in een vaste volgorde aangeboden. Hierdoor is gewaarborgd dat de score van een kandidaat niet afhankelijk kan zijn van bekendheid met de items.

1.4.2. Het schatten van intelligentie in adaptieve tests

 Zoals de meeste adaptieve tests maken we bij de ACT Algemene Intelligentie gebruik van itemresponstheorie (IRT, zie bijvoorbeeld Hambleton, Swaminathan, & Rogers, 1991, en Embretson & Reise, 2000). Het doel van IRT is om de latente (dus niet geobserveerde) score, θ, van iemand op een bepaald construct (in dit geval intelligentie) te meten. Het is belangrijk om op te merken dat IRT-modellen draaien om kans. Gegeven bepaalde karakteristieken van items (bijvoorbeeld de moeilijkheidsgraad en de mate van discriminatie van het item), hoe groot is de kans dan dat iemand deze goed of fout beantwoordt? Het grote voordeel van IRT is dat de kenmerken van personen en items op dezelfde schaal kunnen worden weergegeven.

In de ACT Algemene Intelligentie maken we gebruik van het Two-Parameter Logistic (2PL) Model. De kans op een goed antwoord, x = 1, op een bepaald item, gegeven iemands θ komt overeen met:

(1.1)

Het subscript j geeft aan dat het om een karakteristiek van een persoon gaat. In de vergelijking is b_i de moeilijkheid van een item i, en a_i de discriminatie parameter. De specifieke betekenis van a_i en b_i worden in de volgende secties verder uiteengezet.

Het is belangrijk om hier op te merken dat de waarden van b_i en a_i bekend zijn: deze itemkenmerken zijn op basis van een grootschalig onderzoek (zie sectie 1.5.1.1.) bepaald. Dit betekent dat we voor verschillende waarden van θ kunnen bepalen hoe groot de kans is dat een item goed beantwoordt wordt. Wanneer we verschillende waarden voor θ invullen kunnen we de itemresponsfunctie plotten (zie Figuur 1.1), waarin de ‘kans op een goed antwoord’ afgezet wordt tegen θ.

Figuur 1.1. Itemresponsfunctie.

Deze kansen vormen de basis van de berekening van θ. Gegeven dat er in een test k aantal items zijn, is de likelihood functie van een bepaald responspatroon (bijvoorbeeld ‘goed, fout, goed’, of ‘1,0,1’) gelijk aan:

 (1.2)

Hierbij is Q de kans op een fout antwoord, oftewel 1 – Q. De likelihood van het responspatroon ‘goed, fout, goed’, of ‘1,0,1’, is dus P_item1 x Q_item2 x P_item3.

Op basis van deze likelihood wordt θ geschat: om de waarde van θ te vinden, wordt deze likelihood L gemaximaliseerd (oftewel, gekeken waar de top van deze functie ligt). In de ACT Algemene Intelligentie berekenen we θ door middel van de expected a posteriori methode (EAP). Dit is een Bayesiaanse methode, wat betekent dat we ervan uitgaan dat een persoon (dus θ) getrokken is uit een populatie (met een standaardnormale verdeling met gemiddelde 0 en standaarddeviatie van 1). Dit betekent dat L gewogen wordt met hoe groot de kans is dat we de geschatte θ vinden. Het gaat te ver om hier in detail uit te leggen hoe dit werkt, maar uiteindelijk is het gemiddelde van de nieuwe gewogen likelihood functie (de posterior distribution) de geschatte θ. De standaarddeviatie van deze posterior distribution geeft de spreiding aan die rondom de geschatte θ verwacht mag worden: hoe kleiner deze spreiding, hoe nauwkeuriger de meting. Deze waarde wordt de standard error of measurement (SEM) of standaardfout genoemd. Dit is belangrijk voor de ACT Algemene Intelligentie, omdat deze SEM gebruikt wordt als het stopcriterium van de test (zie sectie 1.5.4). Voor meer informatie over de schatting van θ verwijzen we de geïnteresseerde lezer door naar De Ayala (2013).

De schatting van θ is gebaseerd op de gegeven antwoorden van een persoon. Bij adaptief testen wordt na ieder gegeven antwoord de θ opnieuw berekend met de tot dan toe gegeven antwoorden. De nauwkeurigheid waarmee θ geschat is, wordt aangegeven door de SEM. Als de θ nauwkeurig genoeg geschat is, met andere woorden als de SEM laag genoeg is, stopt de test (zie sectie 1.5.4.).

1.5. Ontwikkeling van de ACT Algemene Intelligentie

Een adaptieve test, zo ook de ACT Algemene Intelligentie, bestaat uit een aantal onderdelen:

1. Itempool met bekende a– en b-parameters (sectie 1.5.1.)
2. Itemselectie (sectie 1.5.2.)
3. Startregel (sectie 1.5.3.)
4. Stopregel (sectie 1.5.4.)

De methode van de θ-schatting is feitelijk ook een onderdeel van een adaptieve test, maar deze is in de voorgaande sectie al besproken (de EAP-methode bij de ACT Algemene Intelligentie). In dit hoofdstuk worden de ontwikkeling van en de gemaakte keuzes voor elk onderdeel van de ACT Algemene Intelligentie en de daarbij behorende onderzoeken apart beschreven. Hiermee wordt de ontwikkeling en ontstaansgeschiedenis van de huidige ACT Algemene Intelligentie over drie opeenvolgende versies (Versie 3 is de huidige versie) besproken.

1.5.1. Itempool

1.5.1.1. Kalibratie-onderzoek

Om een itempool te kunnen creëren, oftewel om de a– en b-parameters van items te kunnen bepalen is eind 2014 een grootschalig onderzoek door Ixly uitgevoerd. Via een ISO-gecertificeerd internetpanel zijn aan in totaal ongeveer 3700 respondenten een groot aantal items voorgelegd.

Deze steekproef[1] bestond voor 41.8% uit mannen en 58.2% vrouwen. Vergeleken met de beroepsbevolking (2013) leek deze verdeling niet geheel representatief (χ² = 15.43, df = 1, p = .00); echter, de effectgrootte φ wees uit dat het hier om een klein verschil in het aantal mannen en vrouwen ging (.06).

De gemiddelde leeftijd was 45.2 (SD = 13.1), variërend tussen de 17-67 jaar oud. Verdeeld over de vier leeftijdscategorieën gehanteerd door het CBS (15 tot 25, 25 tot 40, 40 tot 55 en 55 tot 65) bleek dat de steekproef aardig te vergelijken was met de beroepsbevolking wat betreft leeftijd, waarbij de effectgrootte Cramer’s V duidde op en gemiddeld effect (χ² = 473.17, df = 3, p = .00, V = .21). Personen uit de hoogste leeftijdscategorie waren voornamelijk oververtegenwoordigd, terwijl personen tussen de 25 en 40 ondervertegenwoordigd waren. Echter, omdat het effect van leeftijd op de scores op de ACT Algemene Intelligentie gering is (zie Hoofdstuk 6), zal het effect hiervan op de resultaten waarschijnlijk klein zijn.

Vergeleken met de driedeling van het CBS (laag-midden-hoog, zie Tabel 6.33. in Hoofdstuk 6) verschilde de opleidingsverdeling in de huidige steekproef enigszins van de opleidingsverdeling in de beroepsbevolking (χ² = 157.25, df = 2, p = .00), hoewel het verschil als ‘gemiddeld’ gekwalificeerd kon worden (V = .15). Hoger opgeleiden waren enigszins ondervertegenwoordigd. Deze ruwe indeling verbloemt echter het feit dat de steekproef uit personen van vrijwel alle mogelijke opleidingsniveaus bestond, waarbij er dus geen personen uit bepaalde categorieën over het hoofd gezien zijn.

In Tabel 1.1[2] zijn de regio’s waaruit de personen uit de steekproef afkomstig waren weergegeven. In de vierde kolom staat de verdeling over de provincies voor de beroepsbevolking weergegeven. Wat opvalt is dat de percentages uit de derde en vierde kolom nauwelijks verschillen. Een formele statistische toets wees uit dat, hoewel er significante verschillen waren, de steekproef voldoende representatief was wat betreft regio (χ² = 91.44, df = 11, p = .00, V = .05). Ook waren er niet of nauwelijks verschillen tussen regio’s wat betreft scores op de items van Cijferreeksen (F(11,2675) = 1.18, p = .05, η² = .007), Figurenreeksen (F(11,2531) = 1.22, p = .27, η² = .005), Verbale Analogieën (F(11,2357) = 1.97, p = .03, η² = .009) en de daarop gebaseerde g-score (F(11,3713)= 2.01, p = .02, η² = .006). Verschillen in de regio waarin personen woonachtig zijn lijken dus weinig invloed te hebben op de resultaten.

Tabel 1.1. Verdeling over regio’s in kalibratiesteekproef.
	Freq.	%	CBS %
Drenthe	122	3.3	2.8
Flevoland	108	2.9	2.5
Friesland	181	4.9	3.8
Gelderland	426	11.4	12
Groningen	184	4.9	3.3
Limburg	279	7.5	6.4
Noord-Brabant	546	14.7	14.7
Noord-Holland	529	14.2	16.9
Overijssel	222	6.0	6.6
Utrecht	241	6.5	7.6
Zeeland	109	2.9	2.1
Zuid-Holland	778	20.9	21.2

In Tabel 1.2. zijn de sectoren weergegeven waarin de deelnemers werkzaam waren. Deze sectoren zijn de bedrijfssectoren zoals gespecificeerd in de Standaard Bedrijfsindeling 2008 (SBI ’08).

Tabel 1.2. Verdeling over werksectoren (SBI ‘08) in kalibratiesteekproef.
	Freq.	%a	CBS %
A. Landbouw, bosbouw en visserij	55	1.8	2.4
B. Delfstoffenwinning	4	.1	0.1
C. Industrie	266	8.6	11.3
D. Energievoorziening	20	.6	0.5
E. Waterbedrijven en afvalbeheer	7	.2	0.5
F. Bouwnijverheid	136	4.4	6.4
G. Handel	310	10.0	14.0
H. Vervoer en opslag	191	6.2	5.0
I. Horeca	206	6.6	3.4
J. Informatie en communicatie	146	4.7	3.9
K. Financiële dienstverlening	151	4.9	3.2
L. Verhuur en handel van onroerend goed	12	.4	0.9
M. Specialistische zakelijke diensten	79	2.5	7.4
N. Verhuur en overige zakelijke diensten	26	.8	4.6
O. Openbaar bestuur en overheidsdiensten	158	5.1	7.1
P. Onderwijs	165	5.3	7.3
Q. Gezondheids- en welzijnszorg	625	20.2	17.6
R. Cultuur, sport en recreatie	77	2.5	2.0
S. Overige dienstverlening	465	15.0	2.4
Anders	626	–	–
Totaal	3725	100	100
a Het percentage is berekend over het aantal personen waarvan de sectoren niet “Anders” waren.

Een formele statistische toets wees uit dat er verschillen waren wat betreft werksector in de steekproef en de beroepsbevolking, maar gelet op de tabel lijken deze verschillen in absolute zin mee te vallen (het absolute gemiddelde verschil in percentages is 2.4%). De grootste verschillen zijn bij sector M, N en S te vinden, waarbij personen uit de sectoren M en N ondervertegenwoordigd zijn in de huidige steekproef. De oververtegenwoordiging van personen in sector S in de huidige sector komt waarschijnlijk door de naamgeving: personen die hun werk niet goed vonden passen onder de overige sectoren hebben hoogstwaarschijnlijk voor deze sector gekozen, waardoor deze categorie een overschatting van het waren aantal zal vormen.

Er waren slechts kleine verschillen tussen personen uit verschillende sectoren wat betreft scores op Cijferreeksen (F(18,2212) = 3.22, p = .00, η² = .026), Figurenreeksen (F(18,2080) = 3.11, p = .27, η² = .026), Verbale Analogieën (F(18,1984) = 3.62, p = .00, η² = .032) en de daarop gebaseerde g-score (F(18,3080)= 5.63, p = .00, η² = .032). Gebaseerd op de effectgrootten lijken over het algemeen verschillen in sectoren waarin personen werkzaam waren weinig invloed te hebben gehad op de resultaten van het onderzoek.

De bovenstaande resultaten in ogenschouw nemend kunnen we concluderen dat de steekproef waarop de itemkalibratie is gebaseerd is voldoende representatief is geweest voor de beroepsbevolking van Nederland.

Er werden items van de Figurenreeksen, Cijferreeksen en Verbale Analogieëntest voorgelegd. Om de parameters goed te kunnen schatten werd ervoor gezorgd dat er overlap was tussen de items die de verschillende respondenten kregen. Het design zag er dus, schematisch weergegeven, als volgt uit:

	Boekje 1	Boekje 2	Boekje 3	etc.
Groep 1
Groep 2
Groep 3
etc.

Noot. Iedere ‘groep’ bestond uit ongeveer 150 personen.

‘Boekjes’ zijn verzamelingen van 12-18 items.

We hebben deels gebruik gemaakt van een ‘targeted design’: dat wil zeggen dat ‘makkelijkere’ items met name voorgelegd werden aan personen met lagere opleidingsniveaus en ‘moeilijkere’ items aan personen met hogere opleidingsniveaus. Hierdoor kunnen de itemparameters nauwkeuriger geschat worden (Eggen & Verhelst, 2011). Er waren echter ook groepen die zowel makkelijkere als moeilijkere items voorgelegd kregen. Zo werd ieder item door mensen met verschillende opleidingsniveaus gemaakt, maar door meer mensen van een bepaald opleidingsniveau. Hier moet overigens ook bij opgemerkt worden dat de moeilijkheid van de items in eerste instantie een inschatting was van de ontwikkelaars (van Ixly): in dit onderzoek moest de moeilijkheid van een item juist duidelijk worden.

In totaal waren 228 items per subtest ontworpen: deze items zijn ontworpen door experts binnen Ixly, allen psychologen met ruime ervaring in de test- en selectiepraktijk. Een deel van de items was bovendien afkomstig van een online platform – te benaderen via de website van Ixly – waar internetgebruikers gratis items konden maken (dit platform heeft slechts enkele weken online gestaan dus qua bekendheid van items moet dit geen probleem vormen), en waaruit bleek dat deze items goed functioneerden (afgaand op het aantal goed/fout). Items werden zo cultuurvrij mogelijk gemaakt: dit is met name van belang voor Verbale Analogieën, waar geprobeerd is dit te ondervangen met eenvoudige woorden die de meeste mensen zullen kennen (zie sectie 1.3.3. voor meer informatie hierover). Sommige items bevatten wel wat moeilijkere woorden en zullen dus ook wat moeilijker zijn (zie ook de discussie in sectie Verbale Analogieën hierover). Voor ieder item kreeg men 45 seconden de tijd: het helemaal niet instellen van een tijd kan ertoe leiden dat mensen antwoorden op gaan zoeken of zeer lang over een item doen, wat de kans vergroot dat ze het item correct zullen beantwoorden. Aan de andere kant zou een te korte tijd ertoe kunnen leiden dat mensen gestrest zouden raken, wat niet wenselijk is omdat de test intelligentie dient te meten en niet speededness of snelheid. Vandaar dat we voor een vrij ruime tijdsspanne van 45 seconden hebben gekozen. Door elk item dezelfde tijd mee te geven kan het beschouwd worden als een extra kenmerk dat constant is over alle items.

Iedere persoon kreeg in totaal tussen de 24 en 36 items voorgelegd van verschillende itemtypen. Dit resulteerde erin dat ieder item door ongeveer 300 personen gemaakt werd (de verschillende ‘groepen’ in bovenstaande schematische weergave); hoewel er niet één vuistregel voor steekproefgrootte voor itemkalibratie te destilleren is uit de zeer omvangrijke IRT-literatuur, is er uit onderzoek wel gebleken dat voor het schatten van itemparameters met behulp van IRT-modellen dit het minimale aantal lijkt (Chuah, Drasgow, & Leucht, 2006). Dit resulteerde uiteindelijk in een totale steekproef van 2707, 2565, en 2545 personen voor Cijferreeksen, Figurenreeksen en Verbale Analogieën.

1.5.1.2. Pre-screening

Allereerst werden de items gescreend op de p-waarden (percentage goed). Items die te makkelijk (p > 90%) of te moeilijk (p < 10%) waren werden verwijderd. Ook hebben we voor elk item gekeken of de assumptie van stijgende monotoniciteit door de data ondersteund werd. IRT-modellen veronderstellen namelijk dat de kans dat een item goed beantwoord wordt groter wordt naarmate θ hoger is. Een manier om deze assumptie te testen, is door te kijken naar gemiddelde itemscores als een functie van iemands restscore. De restscore is de totale ruwe schaalscore minus de score op het item dat onderzocht wordt. Door de grafieken van deze functies te bekijken zijn de items die te ver afweken van deze assumptie ook verwijderd. Ten slotte hebben we gekeken naar de inter-item correlaties: als alle items intelligentie meten, dan dienen deze allen positief te correleren. Items die uitsluitend negatieve relaties met andere items hadden werden ook verwijderd. In deze eerste fase zijn we niet te streng geweest: kleine afwijkingen van bovenstaande assumpties werden geaccepteerd. We hebben hiervoor gekozen om eerst een brede itembank te kunnen opbouwen, waar daarna eventueel items nog uit verwijderd zouden kunnen worden op basis van andere fitwaarden. Uiteindelijk bleven er voor Cijferreeksen 211 items over, voor Figurenreeksen 187 en voor Verbale Analogieën 214.

1.5.1.3. Item-kalibratie

 Voor deze overgebleven items werden met behulp van het programma IRTPRO (Paek & Han, 2012) de a– en b-parameters bepaald; dit programma gebruikt een algoritme dat rekening houdt met de missende waarden in de data. Echter, eerst moesten we bepalen welk IRT-model we zouden moeten hanteren.

1.5.1.4. Keuze van het IRT model

 Voor de keuze van het IRT model hebben we de fit van verschillende IRT-modellen vergeleken. Deze fit is uitgedrukt in -2loglikelihood waarde die χ²-verdeeld is. De -2loglikelihood-waarde is gebaseerd op de hoogte van de likelihoodfunctie zoals beschreven in sectie 1.4.2. Door het grote aantal producten wordt deze waarde zeer klein, daarom wordt deze getransformeerd naar een nieuwe schaal door het logaritme te nemen van de uitkomst. Als deze vervolgens met -2 vermenigvuldigd wordt dan volgt deze waarde de χ²-verdeling, waardoor deze gebruikt kan worden voor hypothese toetsen. Door te kijken of de -2loglikelihood waarden van de modellen significant van elkaar verschillen, kunnen we dus bepalen welk model de beste beschrijving van de data geeft.

Het eenvoudigste IRT model is het Rasch model, waar a in formule (1.1.) gelijk is aan 1. Dan is er het 1 Parameter Logistisch (1PL) model waar a niet gelijk aan 1 is, maar wel voor elk item gelijk. Vervolgens is er het 2PL model, waar a voor elk item een andere waarde kan hebben. Ten slotte is er het 3PL model, waar een gok-parameter is toegevoegd, maar onze steekproefgrootte (ongeveer 300 personen per item) is te klein om die parameter betrouwbaar en efficiënt te schatten. Bovendien bestaat in de literatuur enige discussie over de relatief strenge aannames van het 3PL-model die in de praktijk vaak moeilijk te bevredigen zijn, over de theoretische betekenis van gokken op zich – en hoe dit te modeleren (zie De Ayala, 2013, Von Davier, 2009 en Chiu en Camilli, 2013 voor een discussie over deze punten). Om deze redenen hebben we alleen de Rasch, 1PL en 2PL modellen met elkaar vergeleken.

Tabel 1.3. Vergelijking IRT modellen.
Model	Cijferreeksen		Figurenreeksen		Verbale Analogieën
	-2llh	Δ-2llh	-2llh	Δ-2llh	-2llh	Δ-2llh
Rasch	66846.74		64986.67		63564.31
1PL	66756.18	90.56	64954.17	32.50	63131.69	462.62
2PL	65229.23	1526.95	63732.43	1221.74	60953.04	2178.65
Noot: -2llh = -2loglikelihood.

Voor alle drie de subtests bleek het 2PL model de beste beschrijving van de data. Aan de hand van de Figurenreeksentest als voorbeeld zullen we dit hier kort toelichten:

Het verschil in -2loglikelihood waarden tussen het Rasch model en 1PL model is (64986.67 – 64954.17 =) 32.5. Het verschil in vrijheidsgraden is 1: de a-parameter was eerst gelijk aan 1, maar dient nu geschat te worden door het model (maar is wel voor elk item gelijk). Dit verschil is significant (χ²(1) = 32.5, p < .001): het 1PL model is dus significant beter dan het Rasch model. Vervolgens hebben we bekeken of het 2PL model beter is dan het 1PL model. Het verschil in -2loglikelihood waarden is (64954.17 – 63732.43 =) 1221.7. Het verschil in vrijheidsgraden is 186: in het 1PL model moest er slechts één a-parameter geschat worden (voor elk tem gelijk), in dit model voor ieder item één. Ook dit verschil was significant (χ²(1) = 1221.7, p < .001): het 2PL model is dus de beste representatie van de werkelijkheid. Dit model is dan ook gebruikt om de a– en b-waarden te schatten. Hetzelfde gold voor de overige twee subtests (zie ook Tabel 1.3.).

1.5.1.5. Item-fit

Enkele items lieten extreme, onrealistische waarden voor a (5 < a < 0) en b (4 < b < -4) zien. Deze items werden verwijderd. De resterende items zijn toen onderworpen aan een fit-analyse. Hiervoor hebben we gekeken naar de Q₁ waarde van Yen (1981). Deze fitwaarde geeft een indicatie van in hoeverre de geobserveerde data overeenkomt met het model zoals weergegeven in Figuur 1.2. Specifiek wordt de Q₁ waarde berekend door de θ schaal op te delen in 10 categorieën: vervolgens wordt er voor elke categorie gekeken wat de proportie personen is die het item goed heeft. Deze proportie kan vergeleken worden met de verwachte proportie op basis van formule (1.1.) en Figuur 1.2. Komen deze niet overeen, dan is de Q₁ waarde groot: omdat de Q₁ waarde een χ²-verdeling heeft kan deze waarde statistisch getoetst worden. Echter, omdat deze χ²-verdeling mede afhankelijk is van steekproefgrootte (en van het aantal mensen in de categorieën), hebben we ook visuele inspecties gedaan van zogenaamde fitplots (Kingston & Dorans, 1985). Deze zijn weergegeven voor twee Cijferreeksen-items in Figuur 1.2.

Figuur 1.2. Item-fit plots.

Het rechter item is een ‘goed’ item: de χ² waarde is 7.04 en niet significant verschillend van nul. Dit is ook te zien aan de verwachte (blauwe lijn) en geobserveerde (oranje lijn) proporties mensen die het item goed beantwoorden: de twee lijnen verschillen nauwelijks van elkaar. Links is een item waarbij de proporties op basis van het model aanzienlijk verschillen van de geobserveerde proporties. Dit is dus een voorbeeld van een ‘slecht’ item: dat wil zeggen, dit item gedraagt zich niet zoals we op basis van het model mogen verwachten. Elk item hebben we op deze manier geanalyseerd. Om eerder genoemde redenen hebben we onze beslissing om een item te behouden voornamelijk gebaseerd op de visuele inspectie van de fitplots. Hierbij hebben we in eerste instantie gelet op de afstand tussen de geobserveerde en voorspelde proporties (deze mochten niet te ver uit elkaar liggen, zie rechterfiguur 1.2.). Iets grotere afwijkingen aan de uiteinden werden getolereerd; aangezien we hier minder observaties hadden is de kans groter dat hier afwijkingen van het model plaatsvinden.

1.5.1.6. Gestandaardiseerde residuen

In sectie 1.5.1.5. hebben we per item de fit bekeken. Over de gehele itembank kunnen we dit doen door naar de gestandaardiseerde residuen te kijken. Net als bij de Q₁ waarde gaat het hier om het verschil tussen de voorspelde en geobserveerde proporties ‘goed beantwoord’. De gestandaardiseerde residuen zouden, als het model de data goed beschrijft, ongeveer een normale verdeling moeten volgen (Hambleton & Swaminathan, 1985). De verdeling van de gestandaardiseerde residuen voor de drie subtests is weergegeven in Figuur 1.3.

 
Figuur 1.3. Gestandaardiseerde residuen subtests ACT Algemene Intelligentie.

De gestandaardiseerde residuen laten duidelijk een normale verdeling zien. Een formele statistische toets met behulp van de Shapiro-Wilk test gaf alleen voor Verbale Analogieën een indicatie dat de verdeling afweek van de normale verdeling, maar afgaand op Figuur 1.3. lijkt dit in de praktijk mee te vallen (W_CR = .9975, p_CR =.05; W_FR = .9983, p_FR = .33; W_VA = .9913, p_VA =.00). Over de gehele itembank genomen lijken de itemparameters dus bij alle drie de subtests de data goed te beschrijven.

1.5.1.7. De Lz-waarden

 Naast de Q₁-statistiek hebben we per item ook de Lz­-statistiek (Drasgow, Levine, & Williams, 1985) berekend. De L staat hierbij voor likelihood: bij de Lz waarde wordt gekeken hoe hoog de likelihood functie (zie sectie 1.4.2.) precies is. Is deze hoog, dan zijn de gegeven antwoorden, gegeven de geschatte itemparameters dus waarschijnlijk. Dit betekent dat de itemparameters een goede weergave van de werkelijkheid zijn. Is deze waarde laag, dan zijn de gegeven antwoorden onwaarschijnlijk en is er dus geen sprake van itemfit. De Lz-waarden zijn bij benadering normaal verdeeld en kunnen dus met de standaardnormale verdeling vergeleken worden.

Bij Cijferreeksen was de gemiddelde Lz-waarde .86 (SD = .54), variërend van -.04 tot 3.61. Bij Figurenreeksen was de gemiddelde Lz-waarde .86 (SD = .65), met een minimum van .06 en maximum van 4.21. Bij Verbale Analogieën was de gemiddelde Lz-waarde .63 (SD = .39), variërend van -.05 tot 2.06.

Opvallend is het feit dat de Lz-waarden scheef verdeeld zijn met nauwelijks lage waarden en meer hoge waarden. ‘Hoog’ is hierbij wel relatief: alleen bij Cijferreeksen en Figurenreeksen waren er slechts een paar items waarbij Lz > 2.58 (p < .01). Inspectie van deze items toonde aan dat dit veelal de items waren die ook al na de Q₁ inspectie naar voren waren gekomen en als ‘onderzoeksitem’ waren aangeduid. Van de overige items hebben we nogmaals de fitplots bekeken en besloten om ze in de pool te houden. Deze beslissing is mede gebaseerd op het feit dat hoge Lz-waarden over het algemeen minder schadelijk worden geacht dan lage Lz-waarden: in het laatste geval is er sprake van slechte fit, wat invloed kan hebben op de schattingen van θ. Hoge Lz-waarden zijn vaak een indicatie van overtollige (redundant) items en zullen weinig invloed hebben op schattingen van θ (Linacre, 2000). Bij een itempool voor een adaptieve test is het vaak onontkoombaar om items te hebben die op elkaar lijken: sterker nog, het is een goed kenmerk van een itempool als ze items met vergelijkbare moeilijkheid hebben, maar die net even anders zijn (voorwaarde is wel dat de items onafhankelijk van elkaar zijn). Zo kan gegarandeerd worden dat met verschillende items dezelfde goede schatting gedaan kan worden. Wanneer we de Lz-waarden van een item afzetten tegenover hun moeilijkheid, zagen we dat de hogere waarden vooral clusterden rond gemiddelde θ-waarden (tussen de -0.5 en 0.5): aangezien zich hier meer items bevinden is de kans groter dat ze ook meer conceptuele overlap vertonen.

In totaal bleven er na deze analyses voor de Cijferreeksen, Figurenreeksen en Verbale Analogieën tests respectievelijk 196, 168 en 204 items over. De in deze laatste stap afgevallen items werden aangeduid als onderzoeksitems: dit betekent dat deze wel getoond kunnen worden aan kandidaten, maar dat deze niet gebruikt worden om de θ te berekenen. Dit stelt ons in staat om meer data over deze items te verzamelen. De hierop volgende beschrijvingen zijn gebaseerd op de eerder genoemde 196, 168 en 204 items, tenzij anders vermeld.

1.5.2. Itemselectie

 1.5.2.1. Achtergrond

 Na elk gegeven antwoord moet het beste nieuwe item gezocht worden. Het beste item is in dit geval het item dat de meeste informatie geeft op het interim θ-niveau. De informatie voor een item wordt bij het 2PL-model gegeven door:

                                                (1.3)

Uit de formule blijkt dat vooral de discriminatie-parameter, a, belangrijk is. Goed discriminerende items (hoge a-waarden) zorgen voor veel informatie. Stelt u voor dat a = 0 in formule (1.3.): dat wil zeggen dat het niet uitmaakt hoe hoog iemands θ is, maar dat de kans om het item goed te hebben voor alle θ’s gelijk is. Dit wordt duidelijk aan de hand van de Figuur 1.4 waarin de iteminformatiefunctie (IIF) wordt weergegeven (de parabolen). Het blauwe en zwarte item hebben dezelfde b-waarde (= -1), maar het blauwe item heeft een veel hogere a-waarde: dit item levert veel meer informatie (te zien aan de veel hogere top van de blauwe parabool). Het groene item heeft een b-waarde van 2 en dezelfde a-waarde als het zwarte item. De top van de IIF ligt boven de b– parameter, dit is ook logisch: een item is het meest informatief voor personen waarvan het IQ gelijk is aan de moeilijkheid van het item. Of anders gezegd: een heel moeilijk item geven aan iemand met een laag IQ levert weinig bruikbare informatie op.

Figuur 1.4. Iteminformatiefuncties.

Deze hoogte van informatiewaarde vormt de basis van de itemselectie in de subtests binnen de ACT Algemene Intelligentie. In Figuur 1.4 zijn 3 fictieve Cijferreeksenitems afgebeeld (de gestippelde lijnen zijn de bijbehorende itemresponsfuncties), maar voor alle resterende items in de itembank zijn dit soort functies weer te geven: allemaal met een hogere of lagere top op een ander punt op de horizontale as. Stel dat iemand een aantal vragen goed en een aantal fout heeft gehad en zijn/haar interim θ-schatting op θ = -1.5 ligt. Wanneer men op dit punt omhoog gaat in de figuur, dan ziet men dat het blauwe item de hoogste informatie levert: dit zou dus het volgende item moeten zijn. Stel nou dat een ander persoon bijna alle vragen goed heeft gemaakt en zijn interim θ schatting ligt op θ = 2.5. Nu is het groene item het item dat de meeste informatie levert: dit wordt het volgende item voor deze persoon. Bovenstaande beschrijving behoort bij itemselectie op basis van de Maximum Fisher Informatie (MFI) methode. Het nadeel van MFI is dat het de hoeveelheid informatie berekent voor een toekomstig item op het huidige θ-niveau (Veldkamp, 2010). De Maximum Expected Information methode (MEI) houdt rekening met de toekomstige θ als iemand het volgende item goed of fout heeft. Bovendien is in een grootschalige studie aangetoond dat methodes die toekomstige antwoorden meenemen in de informatieberekening, gecombineerd met de EAP methode voor de berekening van θ, het best en meest efficiënt werken (Van der Linden & Glas, 2010). De volgende sectie beschrijft een studie naar de invloed van beide methoden op de meetnauwkeurigheid van de ACT Algemene Intelligentie waarop de itemkeuzemethode is gebaseerd.

1.5.2.2. Onderzoek voor keuze van itemselectie-criterium

Het grote voordeel van IRT-modellen is dat het modelmatig goed te toetsen is met simulatiestudies, wat in de wetenschap dan ook uitvoerig gebeurt (zie bijvoorbeeld Van der Linden en Glas, 2010). We zijn als volgt te werk gegaan. Eerst hebben we uit een normale verdeling N(0,1) een steekproef van 1000 personen (dus θ’s) genomen. Dit zijn de ‘ware θ’s’. Voor elk item in de itembank is vervolgens aan de hand van formule (1) te berekenen wat de kans (P) is dat iemand met deze θ het item goed heeft. Vervolgens wordt deze waarde met een willekeurig getrokken nummer tussen 0 en 1 vergeleken. Is de waarde van P hoger dan het willekeurig getrokken nummer, dan is het item ‘goed’, is de waarde van P lager dan het willekeurige nummer, dan is het item ‘fout’. Zo wordt voor elke persoon (ware θ) een responspatroon gegenereerd.

Vervolgens kan de adaptieve test gesimuleerd worden met de specificaties zoals bijvoorbeeld vermeld in sectie 1.6. Deze specificaties kunnen naar eigen wil aangepast worden om te kijken wat het effect hiervan is op de precisie van de meting. Net zoals in het echt krijgt de ‘persoon’ een item op basis van de beginregel, het antwoord wordt op bovenstaande wijze bepaald, vervolgens volgt een nieuw item volgens de itemselectieprocedure, etc. Omdat er een willekeurig component in de gegenereerde antwoorden zit, hebben we 5 datasets van 1000 personen gegenereerd, bij die personen de gehele ACT Algemene Intelligentie gesimuleerd (dus Cijferreeksen, Figurenreeksen en Verbale Analogieën) en vervolgens – gemiddeld over de vijf datasets – relevante uitkomstwaarden bekeken.

In het ontwikkelstadium van de ACT Algemene Intelligentie hebben we een simulatiestudie uitgevoerd om de beste methode van itemselectie te bepalen in de adaptieve test. De vijf gegenereerde datasets zoals hiervoor beschreven werden hiervoor gebruikt. Ter vergelijking hebben we ook de adaptieve test gesimuleerd waarbij het volgende item volledig at random gekozen werd. Alle simulaties zijn uitgevoerd in ℝ (R Core Team, 2015) met syntax afkomstig uit Firestar-D (Choi, Podrabsky, & McKinney, 2012), aangepast om de kenmerken van de ACT Algemene Intelligentie te weerspiegelen.

De precisie van de metingen werd op basis van vier maten bepaald. Een belangrijke indicatie voor de precisie van de meting is de root mean squared error (RMSE), die het gemiddelde verschil weergeeft tussen de geschatte θ uit de adaptieve test, , en de ware θ, θ_k. Specifiek is de formule:

                                                        (1.4)

Hierbij is n het aantal personen. Lagere waarden van de RMSE betekenen een kleiner verschil tussen de ware θ en geschatte θ, wat dus meer precisie van de meting betekent.

We hebben ook gekeken naar de correlatie tussen de geschatte θ en de ware θ, naar de gemiddelde SEM en naar het aantal gebruikte items om tot een betrouwbare schatting van θ te komen. De resultaten zijn weergegeven in Figuur 1.5. en 1.6. voor Figurenreeksen en Verbale Analogieën: de twee selectiemethoden leiden tot exact dezelfde resultaten bij Cijferreeksen.

 Figuur 1.5. Vergelijking verschillende itemselectie methoden, Figurenreeksen.

 Figuur 1.6. Vergelijking verschillende itemselectie methoden, Verbale Analogieën.

Uit Figuur 1.5. en 1.6. blijkt dat er slechts minieme verschillen zijn tussen de twee itemselectie methoden bij zowel de Figurenreeksen- als Verbale Analogieëntest. In vergelijking met de at random methode zien we dat zowel de MFI en MEI methoden een stuk beter presteren. Over het algemeen was de RMSE iets lager bij de MEI methode dan de MFI methode bij Figurenreeksen, terwijl dit andersom het geval was voor Verbale Analogieën. Voor beide subtests gold dat er iets minder items nodig waren om tot deze nauwkeurigere meting te komen, maar nogmaals, deze verschillen waren nihil. In combinatie met de bevindingen van Van der Linden en Glas (2010) hebben we ervoor gekozen de MEI methode te hanteren. Ook omdat dit, mochten we in de toekomst genoeg data verzamelen om het 3PL model te kunnen hanteren, waarschijnlijk tot meer efficiënte metingen zal leiden. Bovendien zal de meer efficiëntere meting van de MEI-methode tot een betere schatting van θ leiden wanneer er restricties worden opgelegd aan de te tonen items om voor exposure control zorg te dragen. Dit wordt in sectie 1.7 uiteengezet.

1.5.3. Startregel/start-θ

We hebben ervoor gekozen om de start-θ net iets onder het gemiddelde in te stellen, bij θ = -0.5. Op die manier geven wij hen een grotere kans het eerste item goed te beantwoorden, wat de testbeleving ten goede zal komen. De gevolgen van deze keuze ten opzichte van de meer standaard beginwaarde van θ = 0 zijn met simulatiestudies onderzocht; de nauwkeurigheid van de schatting van θ ten opzichte van de ware θ leed niet onder deze keuze.

1.5.4. Stopregel

 De meest gebruikte stopregel in adaptieve tests is stoppen wanneer SEM < x, waarbij x een van te voren bepaald criterium, dus mate van precisie is. We hebben gekozen voor een waarde van 0.39, wat theoretisch overeenkomt met ongeveer een betrouwbaarheid van .85 (1- 0.39² = 0.85; Thissen, 2000) voor elk van de drie subtests. Voor tests voor belangrijke beslissingen – zoals personeelsselectie waarvoor de ACT Algemene Intelligentie ontwikkeld is – is dit ruim voldoende op subtestniveau (> .80; Cotan, 2009). Hierbij moet opgemerkt worden dat de ACT Algemene Intelligentie bestaat uit meerdere, namelijk drie, subtests: de betrouwbaarheid van iedere subtest afzonderlijk is daarbij van belang, maar belangrijker is de betrouwbaarheid van de totaalscore die op basis van alle subtests berekend wordt. Een betrouwbaarheid van een (sub)test van .85 is dus al hoog, maar die van de totale test zal hoger liggen (zie Hoofdstuk 5).

Deze stopregel hebben wij begrensd door een minimum en maximum aantal items in te stellen, namelijk respectievelijk 7 en 12. Rond gemiddelde θ-waarden (dus rond 0) kan het stopcriterium snel bereikt worden – in dit gebied zijn immers veel informatieve items te vinden –, maar een persoon kan aan het begin net een paar foute antwoorden geven die niet echt zijn/haar echte θ weerspiegelen. Om deze ‘fouten’ recht te zetten zal iemand weer wat items nodig hebben. Om mensen niet te veel voor dit soort fouten te ‘straffen’ hebben we het minimum aantal items in eerste instantie op 7 gezet. Om de afnametijd te beperken hebben we het maximaal aantal items in de eerste versie van de ACT Algemene Intelligentie op 12 gezet. Echter, de meeste mensen zullen minder items nodig hebben voor een betrouwbare schatting van θ (zie ook Hoofdstuk 5).

1.6. Specificaties van de ACT Algemene Intelligentie V1

 Iedere subtest begint net onder het gemiddeld niveau (θ = -0.5)

• Itemselectie gebeurt op basis van de Maximum Expected Information-methode
• Schatting van θ op basis van de expected a posteriori methode (EAP)
• Het minimale aantal items is 7, het maximale aantal items is 12
• De test stopt als de SEM < .39 (tenzij er minder dan het minimum aantal, of het maximale aantal items getoond is), wat ongeveer overeenkomt met een betrouwbaarheid van .85 per subtest.

1.7. Onderzoek naar exposure control-methoden en ACT Algemene Intelligentie V2

1.7.1. Achtergrond onder- en overbenutting

 De eerste versie van de ACT Algemene Intelligentie is vanaf februari 2015 een aantal maanden in gebruik geweest door een aantal klanten van Ixly. In deze versie bleken per subtest ongeveer 40 items uit de itembank gebruikt te worden. Dit is een direct gevolg van de gebruikte itemselectiemethode. Het meest informatieve item wordt steeds gekozen om zo snel mogelijk een zo nauwkeurig mogelijke meting van θ te krijgen; in de praktijk zijn dit de items met de hoogste discriminatie-parameters (a, zie Figuur 1.4.). Dit heeft tot gevolg dat een klein aantal items overbenut wordt, terwijl een groot aantal items onderbenut wordt.

Om verschillende redenen is de over- en onderbenutting van de items niet wenselijk waarbij itembekendheid het belangrijkste bezwaar is: door verspreiding op internet zouden de items en hun antwoorden bekend kunnen worden, wat natuurlijk de betrouwbaarheid en validiteit van de test in gevaar zou brengen. Een andere reden is de investering die gedaan is in de itembank: het zou zonde zijn om daar slechts een klein percentage van te benutten. En ten derde is het juist een groot voordeel van IRT-modellen dat de moeilijkheid en discriminerende kracht van items bekend zijn: hierdoor is de intelligentie van personen met verschillende items even nauwkeurig te meten. Het zou zonde zijn om dit kenmerk van IRT niet optimaal te benutten.

1.7.2. Methoden om onder- en overbenutting tegen te gaan

 Om al deze redenen zijn er in de literatuur een aantal methoden ontwikkeld om over- of onderbenutting van items tegen te gaan, ieder met zijn eigen voor- en nadelen (Veldkamp, 2010). Een simpele methode is bijvoorbeeld niet het meest informatieve item te nemen, maar van bijvoorbeeld de 5 meest informatieve items er willekeurig 1 te kiezen. Een andere veel gebruikte methode is bijvoorbeeld de Sympson-Hettermethode (1985), maar het vinden van de juiste controleparameters die daarvoor gebruikt worden is erg tijdsintensief (Veldkamp, 2010). Bovendien moeten deze parameters opnieuw berekend worden bij elke verandering in de itembanken. Daarom hebben we deze methode niet gehanteerd.

Een andere methode is de Progressief Beperkte methode (Revuelta en Ponsoda, 1998). Deze is in eerste instantie ontworpen om onderbenutting van items tegen te gaan en blijkt daarin erg succesvol (Veldkamp, 2010). Het idee is simpel: elke keer als er een item gekozen wordt, dan wordt de informatie die het item levert gewogen aan de hand van de volgende formule en het item met de hoogste waarde getoond:

                                                             (1.5)

waarbij R_i een random nummer is tussen 0 en de informatiewaarde van het meest informatieve item bij de θ op dat moment, s het aantal getoonde items in de test tot dat moment en n het maximale aantal items in de test is. Uit de formule wordt duidelijk dat de random component aan het begin groot is en de informatiecomponent klein, maar dat het omgekeerde het geval is naarmate een kandidaat verder in de test komt.

Uit de formule blijkt ook dat er wel een aantal nadelen aan verbonden zijn: in het begin van de test zal een kandidaat volledig willekeurig een item uit de itembank krijgen, waardoor hij/zij een zeer makkelijk of moeilijk item kan krijgen. Vooral dit laatste zal de testbeleving niet ten goede komen. Bovendien is er geen controle op overbenutting: het is nog maar de vraag of doelen met betrekking tot het maximaal aantal keren dat een item getoond mag worden (bijvoorbeeld ‘in 30% van het totaal aantal tests’) gehaald worden (Veldkamp, 2010).

1.7.3. Onderzoek naar verschillende methoden

Daarom hebben we aan de hand van simulatiestudies varianten van deze Progressief Beperkte (vanaf hier PB) methode getest die deze nadelen beogen te verhelpen, en om de mate van exposure te onderzoeken.[3] De eerste variant is een variant waarbij bovenstaande formule nog gewogen wordt met de exposure rate (ER) van een item tot dat moment (dus het aantal keer dat het item getoond is gedeeld door het aantal keer dat de test is gemaakt). Specifiek wordt bovenstaande formule gewogen met 1-ER: als een item in alle gevallen getoond is (ER = 1) zal de uitkomst van de formule dus 0 zijn en het item per definitie niet getoond worden. Deze aanpassing zorgt ervoor dat overbenutting begrensd wordt. Deze methode wordt vanaf hier aangeduid met 1-er PB.

De tweede variant is de Fuzzy-methode, ontwikkeld door Ixly. Deze methode combineert een aantal kenmerken van verschillende methoden. Zo wordt voor het eerste item de informatie alleen gewogen met 1-exposure rate: met het beoogde resultaat dat het eerste item niet volledig willekeurig getoond wordt maar ongeveer rond de -0.5 ligt (zoals in Versie 1). Bovendien is de random component verkleind door een constante toe te voegen aan het tweede deel van de formule hierboven (na de +). Tot slot wordt elke keer uit de drie items met de hoogste uitkomsten uit de formule er willekeurig één gekozen: dit om overbenutting nog meer tegen te gaan.

Het moge duidelijk zijn dat bij de restricties voor het tonen van items een heleboel verschillende belangen tegelijk spelen: items mogen niet te vaak getoond worden, maar er moet wel nog nauwkeurig gemeten worden, zoveel mogelijk items uit de itembank moeten benut worden, maar kandidaten moeten niet veel te moeilijke of makkelijke items krijgen i.v.m. de testbeleving, de test moet zo kort mogelijk blijven etc. Met al deze punten is zoveel mogelijk rekening gehouden bij het bepalen van de beste methode. Als maximale exposure rate hanteerden we het doel van 40%, dus een item mocht maximaal in 4 van de 10 ingezette tests getoond worden. En omdat alle drie de methoden ervoor zorgen dat er minder nauwkeurig gemeten wordt (het meest informatieve item wordt immers niet altijd meer gekozen) hebben we het maximale items verhoogd naar 15. Dit zorgt er tevens voor dat de test meer de ‘tijd’/mogelijkheid krijgt om informatie te verzamelen over de θ van een persoon. De resultaten wat betreft de nauwkeurigheid van de metingen staan weergegeven in Tabel 1.4.

Tabel 1.4. Resultaten simulatiestudies naar benutting items: nauwkeurigheid.
	RMSE			Gem. SEM			Correlatie ware θ			Aantal items
	Fuzzy	PB	1-er   PB	Fuzzy	PB	1-er PB	Fuzzy	PB	1-er PB	Fuzzy	PB	1-er PB
Cijferreeksen	.36	.36	.37	.36	.36	.37	.94	.94	.93	8.79	8.59	10.06
Figurenreeksen	.38	.38	.39	.38	.38	.38	.93	.93	.92	10.03	9.60	12.12
Verbale Analogieën	.32	.33	.35	.32	.33	.35	.95	.95	.94	7.74	7.81	8.41
g-score	.23	.23	.25	.20	.20	.21	.98	.98	.98	26.56	26.00	30.59
Noot. Waarden in de tabel zijn gemiddelde waarden over de vijf gesimuleerde datasets.

 

De drie methoden verschillen weinig van elkaar wat betreft de nauwkeurigheid waarmee θ gemeten wordt. Opvallend is wel dat er voor de 1-er PB methode relatief meer items nodig zijn dan bij de andere twee methoden (over de gehele ACT Algemene Intelligentie, dus over de drie subtests, ongeveer 5 items) en dat dit niet leidt tot nauwkeurigere metingen. Omdat een doel was de test zo kort mogelijk te laten zijn, viel deze methode dus al af.

In Tabel 1.5. staan de resultaten weergegeven voor het gebruik van de itembanken bij de drie methoden. Opvallend is dat bij zowel de PB als 1-er PR methoden (bijna) geen enkel item onbenut blijft. Bij de Fuzzy-methode is dit 24% bij Cijferreeksen, 23% bij Figurenreeksen en 28% van de respectievelijke itembanken.

Tabel 1.5. Resultaten simulatiestudies naar benutting items: gebruik itembank.
	# Ongebruikte items			Max ER			Min/Max b   1e item
	Fuzzy	PB	1-er   PB	Fuzzy	PB	1-er PB	Fuzzy	PB +   1-er PB
Cijferreeksen	50.2	0.4	0	.31	.45	.27	-.78/.08	-1.79/3.82
Figurenreeksen	42.8	0.2	0	.40	.62	.39	-.77/.22	-3.64/3.87
Verbale Analogieën	60.4	1.2	0	.28	.31	.20	-.65/.20	-1.67/4.18
Noot. Waarden in de tabel zijn gemiddelde waarden over de vijf gesimuleerde datasets.

Wanneer we naar de maximale exposure rates kijken, dan valt op dat deze bij de 1-er PB– methode het laagst zijn, maar dat de waarden weinig verschillen van de Fuzzy-methode. Bij de PB-methode is de maximale exposure rate bij twee van de drie subtest > .40, wat te hoog is. De verdeling van de exposure rates is voor de Cijferreeksentest weergegeven in Figuur 1.7. De items zijn gerangschikt naar exposure rate van hoog naar laag. Uit de figuur blijkt dat de exposure rates van de PB-methode het meest uit balans zijn: er zijn items met vrij hoge waarden en ook een flink aantal met lagere waarden. De 1-er PB-methode laat de meest homogene exposure rates zien. De Fuzzy-methode ligt hier ongeveer tussenin.

Figuur 1.7. Itembenutting bij Cijferreeksen – Simulatie 1.

In de laatste kolommen van Tabel 1.5. zien we dat, omdat het eerste item willekeurig gekozen wordt, elk item uit de itembank kan zijn, dus ook hele makkelijke of moeilijke items: bij de Fuzzy-methode liggen de moeilijkheden van de items mooi rond de beoogde -0.50.

Conclusie

 Dit allemaal samen nemend hebben we de Fuzzy-methode gekozen als methode om over- en onderbenutting van items tegen te gaan. Het enige nadeel van deze methode is dat een deel van de items uit de bank onbenut blijft[4], maar dit is meer een probleem voor Ixly (onnodige investering) dan voor de kandidaten. Als het gaat om de exposure rates is de Fuzzy-methode een van de beste keuzes en in combinatie met de andere criteria de beste keuze. Ook voor itembekendheid hoeft niet gevreesd te worden bij de Fuzzy-methode. In de ACT Algemene Intelligentie V2 is deze methode dan ook geïmplementeerd.

Tot slot nog een opmerking wat betreft de inhoud van de items onder de gekozen controlemethode. Bij adaptieve tests krijgt elke kandidaat andere items gepresenteerd, waardoor het mogelijk is dat bepaalde onderwerpen onvoldoende in de test naar voren komen. Er zijn controlemethoden die hiermee rekening houden (zie bijvoorbeeld Kingsbury en Zara, 1991), en ervoor zorgen dat alle onderwerpen voldoende aan bod komen. Echter, deze mogelijke beperking van adaptieve tests speelt meer een rol bij tests waar duidelijk specifieke onderwerpen of inhoudsdomeinen onderscheiden kunnen worden. Denk hierbij aan een geschiedenistentamen over de Nederlandse geschiedenis na 1945 waar bijvoorbeeld vragen over alle decennia gesteld dienen te worden (in tegenstelling tot een student die alleen vragen krijgt over het decennium 2000-2010 en geen vragen over de andere decennia). Een ander voorbeeld is een overgangstoets voor rekenen op de basisschool waarbij een leerling aan moet tonen genoeg kennis te hebben van zowel breuken, vermenigvuldigen en wortel trekken (en dus niet louter sommen met breuken dient te krijgen).

Bij de ACT Algemene Intelligentie is dit minder relevant omdat er geen specifieke inhoudsdomeinen zijn die in gelijke mate bevraagd dienen te worden. Bij de subtests zijn er wel verschillende logische regels die gevonden dienen te worden, maar er zijn een heleboel verschillende regels die niet te categoriseren zijn in specifieke inhoudsdomein. Daarom hebben wij ervoor gekozen af te zien van een controlemethode met inhoudscontrole.

1.8. Herkalibratie en Versie 3

 Veranderingen in Versie 3

 De tweede versie van de ACT Algemene Intelligentie is van juli 2015 tot en met juli 2016 in gebruik geweest. In juli 2016 zijn nieuwe analyses gedaan op de items met nieuwe data (N = 2532, zie Hoofdstuk 6 voor meer informatie over deze steekproef) verkregen in de voorgaande perioden waarin de test daadwerkelijk in gebruik was. Deze data was afkomstig van klanten van Ixly, die de test gebruikten als onderdeel van selectieprocedures. Opnieuw zijn itemfit-statistieken berekend, maar ook is er geluisterd naar feedback van gebruikers wat betreft itemcontent. Op basis van de informatie verkregen uit deze twee bronnen zijn er een aantal items uit itembanken van de Cijferreeksen en Figurenreeksen tests genomen. Uiteindelijk bleven er 122 items (waarvan 6 ‘onderzoeksitems’) in de itembank van Cijferreeksen over en 126 (waarvan 12 ‘onderzoeksitems’) bij Figurenreeksen. De itembank van Verbale Analogieën bleef ongewijzigd. Alle hierop volgende onderzoeksresultaten zijn verkregen op basis van de itemparameters – en dus de hierop gebaseerde θ’s – zoals vastgesteld bij de herkalibratie in juli 2016.

De itemparameters kwamen overigens sterk overeen met de parameters geschat op basis van de kalibratiesteekproef. De correlaties tussen de a-waarden op basis van de oude en nieuwe kalibratie waren .92, .87 en .94 voor respectievelijk Cijferreeksen, Figurenreeksen en Verbale Analogieën. Voor de b-waarden waren de correlaties respectievelijk .98, .88 en .94. Ook de gemiddelde a-waarden verschilden niet veel van elkaar (oud vs. nieuw; 1.47 vs. 1.37 voor Cijferreeksen, 1.01 vs. 1.02 voor Figurenreeksen en 1.67 vs. 1.65 voor Verbale Analogieën). Hetzelfde gold voor de b-waarden (.12 vs. -.05 voor Cijferreeksen, .83 vs. .59 voor Figurenreeksen en .67 vs. .43 voor Verbale Analogieën). De moeilijkheden werden in de nieuwe kalibratie dus wel steeds wat lager (makkelijker) geschat dan in de aanvankelijke kalibratie.

De invloed hiervan is onderzocht door de θ’s gebaseerd op de eerste kalibratie van de kalibratiesteekproef te correleren met de θ’s gebaseerd op de tweede kalibratie. Deze correlaties waren zeer hoog, .98, .96 en .94 voor Cijferreeksen, Figurenreeksen en Verbale Analogieën. De correlaties tussen de SEM-waarden op basis van beide kalibraties waren respectievelijk .98, .99, en .98.[5]

Omdat de itembanken van Cijferreeksen en Figurenreeksen kleiner werden en informatiever waren voor wat lagere niveaus (zie Hoofdstuk 2), is ervoor gekozen het minimaal aantal items te verhogen naar 10 items, en het maximaal aantal items naar 17. Zo zal er uiteindelijk voor de gehele θ-schaal een nauwkeurige meting gedaan kunnen worden. Om dit te onderzoeken is er weer een simulatiestudie uitgevoerd. Analoog aan de voorgaande simulatiestudies hebben we uit een normale verdeling N(0,1) een steekproef van 1000 personen/ ware θ’s gesimuleerd en responspatronen gegenereerd. Omdat uit voorgaande simulatiestudies bleek dat de resultaten bij de verschillende gesimuleerde steekproeven nauwelijks van elkaar verschilden hebben we niet meerdere steekproeven gesimuleerd. Vervolgens hebben we de adaptieve test met de nieuwe instellingen gesimuleerd bij de 1000 gesimuleerde kandidaten. De resultaten zijn weergegeven in Tabel 1.6.

Tabel 1.6. Resultaten simulatiestudies naar kenmerken ACT Algemene Intelligentie na herkalibratie.
	RMSE	Gem.   SEM	r ware θ	Aantal   items		Min/Max b   1e item	# Ongebruikte items	Max. ER
Cijferreeksen	.35	.36	.94	11.48		-.81/-.12	0	.53
Figurenreeksen	.37	.38	.93	12.99		-.80/.36	0	.46
Verbale Analogieën	.29	.28	.96	10.29		-.52/-.04	52	.24
g-score	.21	.19	.98	34.76		–	–	–

 

Uit Tabel 1.6. komt naar voren dat de aanpassingen niet voor een vermindering van de kwaliteiten van de ACT Algemene Intelligentie hebben gezorgd – sterker, gebaseerd op de RMSE, gemiddelde SEM en correlatie met de ‘ware’ θ kunnen we stellen dat de test nog iets nauwkeuriger meet dan voorheen (vergelijk met Tabel 1.5., kolommen ‘Fuzzy’). Wel zijn er wat meer items nodig om tot deze meting te komen, echter met een gemiddelde van ongeveer 35 items is de test nog steeds zeer kort te noemen. Tot slot kan opgemerkt worden dat verwacht kan worden dat alle items van de kleinere itembanken van Cijferreeksen en Figurenreeksen gebruikt gaan worden.

2PL of 1PL-model

 Bij de herziening in juli 2016 is ook weer gekeken of het 2PL model een betere beschrijving van de data was dan het 1PL model. Op basis van de χ²-toetsen op basis van de -2loglikelihood-waarden (zie sectie 1.5.1.4.) bleek dit het geval, en ook uit de lagere BIC-waarden van het 2PL ten opzichte van het 1PL model (lagere waarden duiden op betere model-fit). Echter, we hebben ook gekeken naar de relatieve efficiëntie (De Ayala, 2013) van de modellen. Relatieve efficiëntie zegt iets over de informatie geleverd door het ene model ten opzichte van het andere model. Specifiek hebben we dit als volgt berekend: voor alle θ-waarden van -3 tot en met 3 (in stapjes van 0.1) hebben we de totale informatie door de itembank geleverd voor respectievelijk Cijferreeksen, Figurenreeksen en Verbale Analogieën. Vervolgens hebben we de ratio Informatie(2PL)/Informatie(1PL) berekend: een ratio >1 betekent dat het 2PL-model over de gehele θ-schaal meer informatie levert dan het 1PL-model, een ratio <1 betekent dat het 1PL-model meer informatie levert dan het 2PL-model. Voor Cijferreeksen gold dat het 2PL-model ongeveer 10% meer informatie opleverde dan het 1PL-model, terwijl voor Figurenreeksen en Verbale Analogieën het 1PL-model juist meer informatie gaf dan het 2PL-model, respectievelijk 5% en 4%.

Daarom zou er enige twijfel kunnen zijn of de keuze voor het 2PL-model de schattingen van θ en de nauwkeurigheid van de ACT Algemene Intelligentie nadelig beïnvloedt. Om dit te onderzoeken is een simulatiestudie uitgevoerd. Er werden 1000 ware θ’s gegenereerd, en vervolgens op basis van deze θ’s werden antwoordpatronen gegenereerd conform het 1PL-model (dus op basis van de itemparameters geschat met het 1PL-model) en conform het 2PL-model. Vervolgens zijn er vier condities gesimuleerd:

1. Een conditie met antwoordpatronen conform het 1PL-model, waarbij de adaptieve test de itemparameters van het 1PL-model gebruikte
2. Antwoordpatronen conform het 1PL-model, waarbij de adaptieve test de itemparameters van het 2PL-model gebruikte
3. Antwoordpatronen conform het 2PL-model, waarbij de adaptieve test de itemparameters van het 2PL-model gebruikte
4. Antwoordpatronen conform het 2PL-model, waarbij de adaptieve test de itemparameters van het 1PL-model gebruikte

Zo werd er dus gekeken wat de invloed van een afwijking van de ‘werkelijkheid’ (bijvoorbeeld in werkelijkheid antwoordpatronen gebaseerd op het 1PL model, maar geschat in de adaptieve test met het 2PL-model) was op de uitkomsten van de ACT Algemene Intelligentie. Ook kon zo vergeleken worden of het 1PL-model simpelweg niet tot betere uitkomsten leidde dan het 2PL-model (vergelijking conditie 1 en 3).

De resultaten van dit onderzoek zijn weergegeven in Tabel 1.7.

Tabel 1.7. Resultaten simulatiestudie naar geschiktheid 1PL versus 2PL model.
	RMSE					Gem. SEM					Correlatie ware θ					EB					Aantal items
	1	2	3	4		1	2	3	4		1	2	3	4		1	2	3	4		1	2	3	4
Cijferreeksen	.39	.48	.35	.49		.39	.36	.36	.39		.93	.88	.94	.88		.83	.83	.85	.81		16	11	11	16
Figurenreeksen	.43	.51	.37	.52		.42	.38	.38	.42		.91	.87	.93	.87		.79	.80	.84	.74		17	13	13	17
Verbale Analogieën	.38	.40	.29	.45		.38	.27	.28	.38		.93	.92	.96	.91		.84	.90	.91	.79		11	10	10	10
g-score	.27	.34	.21	.38		.23	.19	.19	.23		.97	.96	.98	.95		.90	.82	.95	.77		44	34	34	43
Noot. 1 = 1PL met 1PL, 2 = 1PL met 2PL, 3 = 2PL met 2PL, 4 = 2PL met 1PL.
EB = empirische betrouwbaarheid.

 

De resultaten laten zien dat het 2PL-model de beste uitkomsten oplevert: de ware θ wordt het best benaderd, wat blijkt uit de laagste RMSE-waarden en de hoogste correlaties met de ware θ. Bovendien heeft het 2PL-model hier relatief weinig items voor nodig. Een vergelijking van conditie 1 en 4 toont aan dat wanneer het gebruikte model voor de ACT Algemene Intelligentie conform is aan de werkelijkheid (dus of 1PL-1PL of 2PL-2PL), het 2PL-model een betere schatting geeft. Tegelijkertijd toont een vergelijking van conditie 2 en 4 aan dat een schending van de werkelijkheid (dus 2PL-1PL of 1PL-2PL) nadeliger is voor de schatting van θ wanneer in werkelijkheid de antwoorden het 2PL-model volgen terwijl dit geschat wordt met het 1PL-model, dan andersom. De empirische betrouwbaarheid is in dit eerste geval (conditie 4) bijvoorbeeld lager dan in het laatste geval (conditie 2), terwijl de gemiddelde SEM hoger is. De RMSE-waarden en correlatie met de ware θ verschillen weinig van elkaar; echter, het aantal items bij de vierde conditie ligt aanzienlijk hoger dan bij de tweede conditie.

Conclusie

 In deze simulatiestudie is aangetoond dat het 2PL-model bij de ACT Algemene Intelligentie een betere beschrijving van de werkelijkheid is dan het 1PL-model. Deze studie rechtvaardigt dan ook de keuze voor het 2PL-model voor de schatting van de itemparameters van de drie subtests Cijferreeksen, Figurenreeksen en Verbale Analogieën.

1.9. Specificaties van de ACT Algemene Intelligentie V3

 Iedere subtest begint net onder het gemiddeld niveau (θ = -0.5)

• Itemselectie gebeurt op basis van de Maximum Expected Information-methode
• Schatting van θ op basis van de expected a posteriori methode (EAP)
• Het minimale aantal items per subtest is 10, het maximale aantal items is 17
• De test stopt als de SEM < .39 (tenzij er minder dan 10, of al 17 items getoond zijn), wat ongeveer overeenkomt met een betrouwbaarheid van .85 per subtest

Omdat de itemkalibratie is uitgevoerd op de totale steekproef (kalibratiesteekproef en kandidaatssteekproef afkomstig uit de Ixly-database) zullen in het vervolg alle resultaten voor deze totale steekproef besproken worden, alsook van de kandidaatssteekproef. Hier is voor gekozen omdat het in eerste instantie belangrijk is om inzicht te krijgen in de psychometrische kwaliteiten van de items en scores bij de groep waar de itemparameters op gebaseerd zijn. Echter, omdat in deze groep ook personen (namelijk die uit de kalibratiesteekproef) zitten die de test niet adaptief gemaakt hebben en de test onder andere omstandigheden hebben gemaakt dan ‘echte’ kandidaten, is het ook belangrijk inzicht te geven in de kenmerken van de test bij deze laatste groep personen. Directe gebruikers van de test zullen meer belang hechten aan de resultaten onder kandidaten die de test in selectiesituaties hebben gemaakt.

 

[1] Omdat deze steekproef een groot deel uitmaakt van de ‘totale steekproef’ (gecombineerde kalibratiesteekproef en kandidaatssteekproef), die beschreven zijn in sectie 6.8., hebben we hier niet de specifieke verdelingen laten zien voor leeftijd en opleidingsniveau.

[2] Omdat er geen informatie beschikbaar was over regio in de kandidaatssteekproef, en dus alleen van de kalibratiesteekproef, is deze tabel hier wel weergegeven.

[3] In eerdere stadia zijn ook andere methoden overwogen en met simulaties bekeken, zoals de Beperkte methode (Revuelta & Ponsoda, 1998) en de methode beschreven in Veldkamp (2010). Om verschillende redenen vielen deze methoden af en i.v.m. de leesbaarheid zijn deze hier dan ook niet beschreven.

[4] Bij elk van de 5 simulaties, waar hier de gemiddelde resultaten van zijn gegeven, begonnen de items weer met een exposure rate van 0, terwijl in de praktijk dit natuurlijk niet het geval is. In dit opzicht verschillen de simulaties van de realiteit. In de praktijk, ook omdat er een random deel in de formule zitten, zullen er dus zeer waarschijnlijk meer items uit de itembank gebruikt kunnen worden.

[5] Correlaties geven een indicatie van de relatieve verhoudingen tussen variabelen, niet van absolute verschillen. Eventuele absolute verschillen (dat wil zeggen, het feit dat iemand met dezelfde gegeven antwoorden op dezelfde vragen een hogere/lagere score zou behalen op basis van de 2^de kalibratie ten opzichte van de 1^ste) zijn ondervangen door de normen aan te passen. Dit betekent in de praktijk dat de teruggekoppelde, gestandaardiseerde score onveranderd zijn gebleven.

1.10. Kleureninformatie en de ACT Algemene Intelligentie V4

Veranderingen in Versie 4: Kleureninformatie en kleurenblindheid

Achtergrond

Kleureninformatie kan niet door iedereen uniform worden waargenomen. Mensen met een beperking binnen kleurwaarneming kunnen bepaalde kleurencombinaties niet altijd herkennen of onderscheiden (Tanaka, Suetake & Uchino, 2010). Om binnen de ACT Algemene Intelligentie te controleren voor kleurenblindheid is onderzoek verricht naar de verschillende vormen van kleurenblindheid. Hieruit is gebleken dat de twee meest voorkomende vormen van kleurenblindheid vallen onder protanopia en deuteranopia. Onder het kleurenblindheid type protanopia vallen mensen waarbij de kegelsoort “rood” in het oog stoort (protanomalie) of helemaal niets doet (protanoop). Bij het type deuteranopia functioneert de “groene” kegelsoort gebrekkig (deuteranomalie) of niet (deuteranoop)(Tanaka et al., 2010). In beide gevallen ervaren mensen hierdoor problemen met het onderscheid tussen de kleuren in de groene-gele-rode sectie van het kleurenspectrum (Tanaka et al., 2010). Protanopia komt voor bij 2,13% van de Nederlandse bevolking en deuteranopia bij 5,28%. De overige vormen van kleurenblindheid komen bij minder dan 0,01% van de Nederlandse bevolking voor (Accessibility.nl, 2020).

Implementatie

Om te voorkomen dat kleurenblindheid een beperkende rol speelt binnen de ACT Algemene Intelligentie is bij de herziening in februari 2020 per onderdeel gekeken of kleuren van invloed kunnen zijn op de prestatie van de kandidaat. Zowel binnen de categorie cijferreeksen als verbale analogieën is kleur niet van invloed op de prestatie van de kandidaat. Binnen het onderdeel figurenreeksen wordt regelmatig gebruik gemaakt van meerdere kleuren om een onderscheid aan te duiden. Binnen dit onderdeel is per item beoordeeld of het onderscheidend vermogen tussen kleuren van kandidaten met kleurenblindheid (type protanopia of type deuteranopia) beperkingen oplevert. Dit is gedaan met behulp van de extensie RGBlind. RGBlind is een opensource real-time kleurenblindheid simulatietool, ontwikkeld om problemen met kleurenblindheid van het type protanopia en deuteranopia te ondervangen. Door middel van de extensie RGBlind was het mogelijk om te beoordelen of items die meerdere kleuren omvatten voldoende onderscheidend zijn voor kandidaten met kleurenblindheid type protanopia of type deuteranopia (Accessibility.nl, 2020). Hierbij zijn 7 items geïdentificeerd in derde versie van de ACT Algemene Intelligentie die mogelijk als problematisch ondervonden kunnen worden. Bij de herziening in februari 2020 zijn bij de vraag en antwoordopties van deze 7 items (in totaal 34 plaatjes) de kleuren vervolgens zo aangepast, dat het onderscheidend vermogen tussen kleuren binnen een item behouden blijft. Dit is gedaan door de uiterste kleuren te het kleurenspectrum te selecteren, zoals blauw-rood-geel of groen-roze. Dit is vervolgens geverifieerd door middel van de RGBlind extensie. De uiteindelijke kleuren zijn op basis van deze extensie voldoende onderscheidend gebleken. Ondanks dat kleuren anders geïnterpreteerd worden door iemand met protanopia of deuteranopia, heeft dit bij de ACT Algemene Intelligentie dus geen invloed op de prestatie van kandidaten met kleurenblindheid type protanopia of deuteranopia.

 

 

2. Testmateriaal

2.1. Inleiding

In dit hoofdstuk zal het testmateriaal van de ACT Algemene Intelligentie worden besproken. Allereerst worden de kenmerken van de items en itembanken van de subtests besproken. Vervolgens wordt er ingegaan op de afname van de test, eventueel onjuist gebruik van de software en het scoringssysteem.

2.2. Kenmerken van de items en de subtests

2.2.1. Cijferreeksen

 Onderstaand vindt u een voorbeeld van een Cijferreeksenitem.

Figuur 2.1. Voorbeelditem Cijferreeksentest.

Bij de Cijferreeksentest wordt de kandidaat geacht een logisch patroon te herkennen in de getoonde reeks cijfers. Volgens deze logica moet beredeneerd worden welk cijfer op de plek van het vraagteken moet komen. In dit geval is de logica als volgt: het eerste getal wordt vermenigvuldigd met zes, het tweede getal met vijf, het derde getal met vier, het vierde getal met drie; dit moet tot de conclusie leiden dat het vijfde getal met twee vermenigvuldigd dient te worden, waarbij de uitkomst 1440 zal zijn. De derde antwoordoptie is dus de juiste.

Dit is slechts een voorbeeld van de vele logische verbanden die voor kunnen komen: bij een aantal items moet elk getal met een constant getal vermenigvuldigd worden, bij andere items dient er steeds een kleiner of groter getal afgetrokken of opgeteld worden, enzovoorts. Er is ook een aantal items waarbij er eigenlijk twee reeksen in het item verborgen zitten: de kandidaat dient er dan achter te komen dat de reeks steeds een hokje overslaat.

 In Figuur 2.2. staan de informatiewaarde en bijbehorende SEM van de gehele itembank van 122 items van Cijferreeksen weergegeven. Hieruit blijkt dat de items het meest informatief zijn bij een θ van ongeveer -1.5: echter, tussen -1 en 1 bevinden zich ook nog voldoende discriminerende items (zie volgende sectie). De a-parameters lopen van .22 tot en met 3.94, met een gemiddelde van 1.37. Hoe hoger de discriminatiewaarde hoe beter: waarden van .80 of .90 of hoger worden gezien als goede discriminatiewaarden (Swartz & Choi, 2009). In totaal zijn er 79 items, dus ongeveer 65% van de items, met een a > .90. De b-parameters hebben een minimum van -2.17 en een maximum van 4.44, met een gemiddelde van -.05.

Figuur 2.2. Itembank Cijferreeksen.

In Figuur 2.3. zijn de moeilijkheden (b) afgezet tegen de discriminatiewaarden (a) van de items. De items clusteren vooral in het midden en de items met een wat lagere moeilijkheid hebben over het algemeen hogere discriminatie waarden (dit is ook te verwachten op basis van Figuur 2.2.). In selectiesituaties zal men met name geïnteresseerd zijn in een voldoende nauwkeurige meting in het gebied -1 tot en met 1. Er zijn 53 items die in dit gebied liggen, waarvan er 35 (66%) een a-waarde van groter of gelijk aan .90 hebben. Hieruit kunnen we concluderen dat de Cijferreeksen-itembank goede en voldoende discriminerende items bevat.

Figuur 2.3. Discriminatie- (a) en moeilijkheid- (b) parameters Cijferreeksen.

2.2.2. Figurenreeksen

Onderstaand vindt u een voorbeelditem van de Figurenreeksentest.

Figuur 2.4. Voorbeelditem Figurenreeksentest.

Het is bij dit item de bedoeling dat de kandidaat, op basis van wat er in de overige acht vakken is afgebeeld, ontdekt welke van de vier antwoordopties in het lege vak rechtsonder hoort. In dit geval zou de kandidaat moeten inzien dat in elke kolom en elke rij steeds eenmaal een rond gezicht, eenmaal een vierkant gezicht, en eenmaal een gezicht zonder omtrek voorkomt. In de rechterkolom en de onderste rij ontbreekt een gezicht met ronde omtrek. Aan deze voorwaarde voldoen alle vier de antwoordopties. Vervolgens komt in elke kolom en elke rij eenmaal een blije mond, eenmaal een rechte mond en eenmaal een scheve mond voor. Hierdoor valt antwoordoptie B af. Tenslotte komt in elke rij en elke kolom eenmaal open ogen, eenmaal streepjes als ogen en eenmaal boogjes als ogen voor. Hieruit kunnen we concluderen dat antwoord A juist is.

Een aantal van de items van de Figurenreeksen volgen dit format. Er zijn echter nog veel meer itemtypes te onderscheiden. In sommige gevallen vormt de matrix een compleet doorlopend plaatje, en moet de kandidaat deze aanvullen. In andere gevallen worden objecten over de rijen en kolommen bij elkaar opgeteld of afgetrokken, en vereist de test dat de kandidaat dit patroon ontdekt.

In Figuur 2.5. staan de informatiewaarde en bijbehorende SEM van de gehele itembank van 126 items van de Figurenreeksentest weergegeven. Hieruit wordt duidelijk dat de items het meest informatief zijn bij een θ van ongeveer -1.5 á -1, waarbij opgemerkt kan worden dat tussen de -1.5 en 1 de items niet veel van elkaar verschillen wat betreft de geleverde informatie (de SEM-lijn is in dit bereik redelijk vlak). De a-parameters lopen van .25 tot en met 3.46, met een gemiddelde van 1.02. In totaal zijn er 62 items, dus ongeveer de helft van de items, met a > .90. De b-parameters hebben een minimum van -2.18 en een maximum van 4.43, met een gemiddelde van .53.

Figuur 2.5. Itembank Figurenreeksen.

In Figuur 2.6. zijn de moeilijkheden (b) weer afgezet tegen de discriminatiewaarden (a) van de items. Er zijn wat meer moeilijkere dan makkelijkere items in de itembank aanwezig. Ook zijn de items met meer gemiddelde of lagere moeilijkheden wat meer discriminerend.

Er zijn 59 items die in het gebied tussen de θ-waarden -1 en 1 liggen, waarvan er 41 (69%) een a-waarde van groter of gelijk aan .90 hebben. Hieruit kunnen we concluderen dat ook de itembank van de Figurenreeksentest goede en voldoende discriminerende items bevat.

Figuur 2.6. Discriminatie- (a) en moeilijkheid- (b) parameters Figurenreeksen.

2.2.3. Verbale Analogieën

Onderstaand vindt u een voorbeelditem van de Verbale Analogieëntest.

Figuur 2.7. Voorbeelditem Verbale Analogieëntest.

Bij de Verbale Analogieëntest bestaan de opgaven uit woorden die een verband met elkaar hebben, gepresenteerd in een vierkant. Het is aan de kandidaat om het verband te herkennen tussen de twee woorden (de analogie) en deze compleet te maken met twee woorden uit de antwoordopties – of om de twee woorden te vinden uit de antwoordopties die hetzelfde verband met elkaar hebben als de twee gegeven woorden. Dit laatste is het geval bij de getoonde voorbeeldopgave hierboven. Lopen doe je met je voeten, en lezen doe je met je ogen.  Daarom zijn ‘ogen’ en ‘lezen’ de juiste antwoorden.

Ook hier geldt weer dat dit slechts een voorbeeld is, er is een groot aantal verbanden dat tussen de woorden ontdekt kan worden, enkele voorbeelden zijn: tegenstellingen, synoniemen, onderdeel van hetzelfde, gebruiker van, maker van, product van, et cetera.

 In Figuur 2.8. staan de informatiewaarde en bijbehorende SEM van de gehele itembank van 214 items van de Verbale Analogieëntest weergegeven. De piek van de informatie curve ligt rond de .50, wat betekent dat de items het meest informatief zijn bij een θ van .50. De a-parameters lopen van .27 tot en met 4.42, met een gemiddelde van 1.65. In totaal zijn er 168 items, dus ongeveer 79% van de items, met a > .90. De b-parameters hebben een minimum van -2.46 en een maximum van 4.27, met een gemiddelde van .43.

Figuur 2.8. Itembank Verbale Analogieën.

Uit Figuur 2.9. blijkt dat de moeilijkere items, net als bij de andere twee subtests, over het algemeen wat lagere discriminatiewaarden hebben. De meest discriminerende items liggen rond het gemiddelde, tussen de -0.5 en 0.5.

Er zijn 139 items die in het gebied tussen de θ-waarden -1 en 1 liggen, waarvan er 123 (88%) een a-waarde van groter of gelijk aan .90 hebben. Hieruit kunnen we concluderen dat ook de itembank van de Verbale Analogieën voldoende discriminerende items bevat in het relevante bereik voor de testdoeleinden.

Interessant is ook dat een aantal zeer discriminerende items zich rond een θ van 1.5 bevinden. Dit is terug te zien in Figuur 2.8. aan de kleine ‘hobbel’ rond deze θ in de informatiegrafiek.

 Figuur 2.9. Discriminatie- (a) en moeilijkheid- (b) parameters Verbale Analogieën.

2.3. Kenmerken van de gehele ACT Algemene Intelligentie

 Wanneer we naar de drie itembanken kijken in Figuren 2.2., 2.5. en 2.8. dan zien we dat de drie subtests qua moeilijkheid een mooie spreiding laten zien rond de θ-waarden waar de meest discriminerende items liggen: bij Cijferreeksen is dit rond θ-waarden van -1.5, bij Figurenreeksen is dit een breed bereik van ongeveer -1.5 tot 1 en bij Verbale Analogieën tussen de -0.5 en 0.5. Zo dekken de drie tests samen dus goed de relevante θ-waarden. Dit gezegd hebbende, is het feit dat met name bij Cijferreeksen en Figurenreeksen het zwaartepunt bij lagere niveaus ligt een punt van aandacht: in de toekomst zullen er daarom meer en beter discriminerende items op hogere niveaus voor deze subtests ontwikkeld en onderzocht worden.

Wanneer we de discriminatiewaarden en de informatie- en SEM-waarden van de itembanken van de drie subtests vergelijken dan zien we dat de items van Verbale Analogieën ‘het best’ zijn: de informatiewaarden zijn voor deze itembank het hoogst (en dus ook de SEM-waarden het laagst over de gehele θ-schaal genomen). De items van Figurenreeksen leveren de minste informatie op. Het is belangrijk hierbij op te merken dat deze subtests uiteindelijk leiden tot een g-score: hoewel een meting van een subtest afzonderlijk meer of minder betrouwbaar zal zijn, zal de schatting van de g-score, doordat deze tot stand komt op basis van drie subtests, zeer betrouwbaar zijn (zie ook Hoofdstuk 5, Betrouwbaarheid).

Om hier meer inzicht in te krijgen zijn de informatie- en SEM-waarden van de totale itembank van de ACT Algemene Intelligentie (dus alle items van Cijferreeksen, Figurenreeksen en Verbale Analogieën samen) weergegeven in Figuur 2.10. Uit dit figuur blijkt dat, over het geheel genomen, de meeste informatie aanwezig is bij gemiddelde θ-waarden (het minimum ligt ongeveer bij -0.5), en dat de minste informatie aanwezig is bij extreem hoge of juist lage θ-waarden. Over het algemeen kunnen we echter concluderen dat er genoeg informatie beschikbaar is om over de gehele θ-schaal nauwkeurig te kunnen meten (zie Hoofdstuk 5).

Figuur 2.10. Totale itembank ACT Algemene Intelligentie

In termen van fluid en crystallized intelligentie zal de g-score met name fluid intelligentie meten: zoals eerder aangegeven is door de kenmerken van de items zoveel mogelijk de invloed van crystallized intelligentie beperkt. In de literatuur worden metingen van g ook beschouwd als metingen van fluid intelligentie en de g-score die tot stand komt op basis van de ACT Algemene Intelligentie vormt hierop geen uitzondering.

2.4. Instructie voor de testafname

2.4.1. Afname

 Alle vragenlijsten die Ixly aanbiedt worden afgenomen in de Test Toolkit (zie Figuur 2.11.). Dit is een online applicatie die aan professionals en consultants op het terrein van Human Resource Management een set kwalitatieve instrumenten biedt. De portal is in principe te bereiken vanaf elke computer of laptop en in iedere browser. Adviseurs loggen in met een gebruikersnaam en een wachtwoord. Vervolgens maken zij een kandidaat in het systeem aan, waaraan zij verschillende tests kunnen toewijzen, waaronder de ACT Algemene Intelligentie. Na het toewijzen van de test nodigt de adviseur de kandidaat uit om de test te maken. De kandidaat krijgt de uitnodiging per e-mail, met daarin een unieke link naar de testomgeving.

Voor de handleiding voor de adviseurs, zie Bijlage 2.1. De informatie over de bediening van de testportaal zijn ook te raadplegen via de Test-Toolkit Tutorials en de Test-Toolkit FAQ

Figuur 2.11. Overzichtsscherm kandidaten.

Instructie

Wanneer de kandidaat op de unieke link in de e-mail heeft geklikt dan komt hij/zij in zijn/haar testomgeving waarin alle toegewezen tests klaar staan. De kandidaat start met een openingsvragenlijst waarin gevraagd wordt informatie te geven over achtergrondvariabelen zoals leeftijd, geslacht en opleiding. Deze gegevens worden uitsluitend voor onderzoeksdoeleinden gebruikt. Voordat de kandidaat start met het maken van de ACT Algemene Intelligentie krijgt hij/zij een duidelijke instructie aangeboden.

Figuur 2.12. Instructies – Scherm 1.

 Figuur 2.13. Instructies – Scherm 2.

Omdat uit onderzoek is gebleken dat het uitleggen van hoe een adaptieve test werkt belangrijk is voor de testbeleving van de kandidaat (zie ook Hoofdstuk 1, sectie 1.4.1.) hebben wij ervoor gekozen dit in de instructies te doen (zie Figuur 2.12., instructiescherm 1). Echter, om de tekst voor iedereen begrijpelijk te houden (gezien het doel van cultuurvrij testen), is deze uitleg kort en in simpele taal – dus zonder technische of statistische termen – gedaan. Andere punten die genoemd worden zijn (zie Figuur 2.12. en 2.13.):

• Iedere subtest wordt voorafgegaan door een voorbeeldopgave en drie oefenopgaven
• De tijd per item (45 seconden)
• Wat ongeveer de totale testtijd zal zijn (40 minuten maar meestal korter)
• Wanneer er gepauzeerd kan worden
• Een niet gegeven antwoord wordt als fout gerekend
• Er mag een kladblok gebruikt worden bij het maken van de test

Voorbeeldopgave en oefenopgaven

Voor iedere subtest verschijnt een voorbeeldopgave en drie oefenopgaven. De voorbeeldopgave voor Cijferreeksen is weergegeven in Figuur 2.15.

Figuur 2.15. Voorbeeldopgave Cijferreeksen.

Bij de voorbeeldopgave wordt een uitleg gegeven van het goede antwoord (Figuur 2.14). Bij de oefenopgaven wordt alleen aangegeven of het gegeven antwoord goed of fout is. Hoewel bekend is dat het geven van feedback kandidaten helpt te begrijpen wat er van hem/haar verwacht wordt, zijn er verschillende redenen om aan te nemen dat de kandidaat voldoende informatie krijgt om de test te begrijpen:

1. Er wordt een voorbeeldopgave met uitleg gegeven.
2. De oefenopgaven hebben geen tijd, waardoor kandidaten er zo lang over kunnen doen als ze willen.
3. Ook de melding ‘Helaas, dit antwoord is fout’ of ‘Dit is het goede antwoord’ blijft staan, wat kandidaten zo veel tijd geeft als ze willen om te begrijpen waarom het door hem/haar gegeven antwoord goed of fout was.
4. Door zelf hierachter te komen en zelf de logica te vinden – wat na de oefenopgaven ook in de subtest zelf dient te gebeuren – traint de kandidaat voor de ‘echte’ test.

Na de oefenopgaven volgt een tussenscherm om de kandidaat erop te wijzen dat de subtest op de volgende pagina begint (Figuur 2.16.).

Figuur 2.16. Scherm voor subtest.

Na iedere subtest verschijnt een tussenscherm om aan te geven dat de kandidaat dan even pauze kan nemen en dat de instructies voor de volgende subtest op de volgende pagina beginnen (Figuur 2.17.).

Figuur 2.17. Tussenscherm.

Aan het eind van de test wordt de kandidaat gevraagd op ‘Afronden’ te klikken, zodat de resultaten opgeslagen worden. De kandidaat wordt dan weer doorverwezen naar zijn/haar overzichtsscherm, waar hij/zij eventueel nog andere tests kan starten. De adviseur kan vervolgens in zijn/haar kandidatenoverzicht het rapport voor de betreffende kandidaat opvragen (zie Hoofdstuk 3).

2.4.2. Voorkomen onjuist gebruik van de software

Het is voor de testgebruiker niet noodzakelijk om verdere voorzorgsmaatregelen te treffen ten aanzien van het voorkómen van fouten. Zo hoeven andere programma’s bijvoorbeeld niet afgesloten te worden tijdens het invullen van de test. Ook hoeven de voorzorgsmaatregelen die genoemd worden door de Cotan (2009) (overbodige functies en sneltoetsen uitschakelen, de toegang tot de harde schijf afsluiten en het onmogelijk maken andere (niet-bedoelde) software op te starten) niet getroffen te worden. Deze kunnen immers geen effect hebben op het invullen van de test en de scoring. Ook dit betekent weer dat de invloed van externe factoren op het invullen van de test beperkt is, waardoor de omstandigheden van het invullen van de test voor iedereen nagenoeg gelijk zal zijn. Wel is er een aantal minimum systeemeisen, deze zullen worden besproken in Hoofdstuk 3, Handleiding voor testleiders.

De ACT Algemene Intelligentie is ontwikkeld voor de selectiepraktijk. Een aantal jaren is de trend gaande dat er door bedrijven steeds meer gekozen wordt in een vroeg stadium van het selectieproces tests door kandidaten thuis te laten maken. De kandidaat maakt de test dan dus in een niet-gesuperviseerde (‘unproctored’) omgeving; dit staat in tegenstelling tot ‘proctored’ tests, bijvoorbeeld in een testzaal waar een testleider aanwezig is. Aangezien de ACT Algemene Intelligentie een test is die via de computer/het internet afgenomen wordt, kunnen gebruikers de afweging maken de test zowel gecontroleerd als ongecontroleerd af te laten nemen.

Hoewel deze keuze aan de gebruiker zelf is, willen we hier stilstaan bij mogelijke afwegingen bij deze keuze. Los van praktische, juridische en ethische bezwaren die geuit zijn, zijn er voornamelijk zorgen  over de validiteit van testscores verkregen in een ‘unproctored’ omgeving (Tippins et al., 2006; Pearlman, 2009). De grootste bedreiging voor testscores verkregen onder zulke condities is de mogelijkheid tot ‘valsspelen’: kandidaten kunnen bijvoorbeeld hulp inschakelen van een vriend, het antwoord opzoeken op internet of zelfs een heel ander persoon de test laten maken (Tippins et al., 2006). Interessant genoeg zijn er onderzoeken die geen verschillen vinden tussen scores verkregen onder ongecontroleerde en gecontroleerde condities (Oswald, Carr, & Schmidt, 2001), studies die vinden dat scores in ongecontroleerde condities hoger zijn (Beaty, Fallon, & Shepherd, 2002; Do, Shepherd, & Drasgow, 2005) en studies die juist hogere scores onder gecontroleerde condities vinden (Shepherd, Do, & Drasgow, 2003; Nye, Do, Drasgow, & Fine, 2008). Recent onderzoek lijkt er echter op te wijzen dat de validiteit van ‘unproctored’ testscores niet in het geding is, ook in ‘high-stakes’ situaties zoals selectieprocedures en ook in het geval van cognitieve tests (Arthur, Glaze, Villado, & Taylor, 2010; Beaty, Nye, Borneman, Kantrowitz, Drasgow, & Grauer, 2011; Kantrowitz & Dainis, 2014).

Er lijken wel optimale condities te zijn waaronder de validiteit van ‘unproctored’ tests het best gewaarborgd zijn (dat wil zeggen waar de kans op ‘valsspelen’ geminimaliseerd is). Zo is de kans hierop kleiner wanneer de ‘unproctored’ test niet te lang is (Tippins et al., 2006). Onderzoek heeft verder aangetoond dat verschillen geminimaliseerd zijn wanneer items tijdgebonden zijn (Kantrowitz & Dainis, 2014; Tippins et al., 2006). Ook is het hebben van een verificatietoets, die bedoeld is om de behaalde scores en hiermee de identiteit van de kandidaat uit de ‘unproctored’ test te bevestigen, wenselijk (Tippins et al., 2006). Adaptief testen, waardoor iedere kandidaat in principe een andere test kan krijgen, zorgt ervoor dat het voor kandidaten minder zin heeft antwoorden op te zoeken. Ook zorgt het hebben van een grote itembank voor een vermindering van itembekendheid. Zo kan adaptief testen bijdragen aan de veiligheid en betrouwbaarheid van de test (De Ayala, 2013; Kantrowitz & Dainis, 2014).

De ACT Algemene Intelligentie voldoet aan de bovengenoemde condities, waardoor we mogen verwachten dat de validiteit van de behaalde scores niet in het geding zullen komen.[2] De items van de ACT Algemene Intelligentie zijn tijdsgebonden en worden adaptief aangeboden. Bovendien is de test relatief kort – gemiddeld ongeveer 30 tot 40 minuten voor de gehele test. Ook is er een verificatietoets beschikbaar waarmee de identiteit van de kandidaat bevestigd kan worden.[3] In theorie zou het mogelijk zijn om screenshots te maken van de items om ze later te delen met anderen, echter, gezien het feit dat verschillende personen andere items krijgen is het effect hiervan te verwaarlozen.

Verder zou de kandidaat de test tussentijds afsluiten om tijd te winnen, maar dit levert niet direct voordeel op, aangezien de tijd van het item doorloopt. Als een kandidaat de vragenlijst tussentijds toch heeft verlaten (wat wij in de instructies afraden) kan hij/zij deze in principe weer opstarten door naar de link te gaan uit de uitnodigingsemail. In eerste instantie wordt het overzichtsscherm getoond, achter de naam van de vragenlijst is een ‘Doorgaan’ knop zichtbaar. De kandidaat gaat dan echter niet verder waar hij/zij gebleven is, maar de tijd loopt door tot de volgende opgave. Zo is het dus niet mogelijk langer de tijd te nemen voor een opgave dan de bedoeling is.

De kandidaat kan, vanzelfsprekend, niet terug naar eerdere opgaven (het drukken van ‘Vorige’ in de browser heeft geen effect): wanneer een antwoord gegeven is dan wordt dit antwoord opgeslagen in de database, en kan niet meer veranderd worden. Alle bovengenoemde kenmerken van de test, instructies en de inrichting van het testsysteem zorgen ervoor dat de invloed van externe factoren op de totstandkoming van scores geminimaliseerd is.

2.4.3. Scoringssysteem

Hoe de adaptieve procedure precies verloopt – dus hoe de antwoorden van de kandidaten uiteindelijk resulteren in intelligentieschattingen – is uitgebreid beschreven in Hoofdstuk 1. Daarin worden de keuzes en onderbouwingen voor de start-, itemselectie-, en stopprocedure van de ACT Algemene Intelligentie toegelicht.

De omzetting van de ruwe scores (goed/fout) naar θ’s en vervolgens naar standaardscores is volledig geautomatiseerd. Er kunnen hierbij dus geen fouten optreden door een verkeerde interpretatie van de testleider. Om fouten door verkeerde invoer van de testontwikkelaars van Ixly te voorkomen worden strenge procedures gevolgd voordat een vragenlijst of test voor klanten beschikbaar is. Deze procedure staat beschreven in het kwaliteitshandboek dat is opgesteld in het kader van de ISO 9001 certificering. Kortweg komt deze procedure er op neer dat de test voor publicatie uitgebreid getest wordt waarbij gecontroleerd wordt of bij elke stap in de ACT Algemene Intelligentie (1) de informatiewaarden van de items – waarop de itemselectie gebaseerd is – kloppen (2) de θ goed berekend wordt en (3) de SEM goed berekend wordt. Dit wordt gecontroleerd door bovenstaande punten uit het Ixly testsysteem te vergelijken met resultaten uit R, waarin de ACT Algemene Intelligentie nagebootst kan worden. Hierbij moet opgemerkt worden dat het testen van een adaptieve test met een randomiseeralgoritme voor de itemselectie uitdagender is dan het testen van een ‘normale’, lineaire test: een standaard testprotocol is door het willekeurige element helaas niet op te stellen. Voor de omzetting van θ’s naar de g-score en de genormeerde scores is er een testbestand aanwezig waarin deze omzetting gecheckt kan worden.

De procedure wordt door verschillende ontwikkelaars uitgevoerd. Een ontwikkelaar doet de test in het online testsysteem van Ixly en een tweede ontwikkelaar checkt de resultaten in R en of de θ’s goed omgezet worden naar de g-score en de genormeerde scores. Wanneer de procedure foutloos is doorlopen wordt de vragenlijst beschikbaar gesteld voor klanten.

2.4.4. Beveiliging van de test, het testmateriaal en testresultaten

Hiervoor is al gerefereerd aan de kenmerken van de ACT Algemene Intelligentie die de validiteit van de testresultaten moeten waarborgen. Er zijn ook kenmerken van het testsysteem die hieraan bijdragen.

De vragenlijst wordt door een adviseur voor de kandidaat klaargezet. De kandidaat ontvangt per e-mail een unieke link en kan daarmee inloggen in het systeem. Het is de verantwoordelijkheid van de adviseur dat het juiste email-adres wordt ingevoerd, zodat de link bij de kandidaat terecht komt.

De beheermodule waarin de gegevens opgeslagen zijn – evenals de itemparameters en de itembanken – is alleen toegankelijk voor R&D’ers van Ixly met een unieke combinatie van gebruikersnaam en wachtwoord die regelmatig verandert.

Nadat de vragenlijst door de kandidaat is ingevuld, ontvangt de adviseur een melding dat de resultaten beschikbaar zijn. De rapportage waarin de resultaten vermeld staan is beschikbaar in de omgeving van de adviseur en dus alleen benaderbaar met de unieke combinatie van gebruikersnaam en wachtwoord van de betreffende adviseur. We bieden adviseurs wel de mogelijkheid om de rapporten direct beschikbaar te maken voor de kandidaat: dit is echter niet standaard het geval, hiervoor moet eerst een handeling verricht worden door de adviseur. Ook bieden wij adviseurs de mogelijkheid om teksten in het rapport aan te passen, maar de behaalde scores kunnen nooit aangepast worden.

Ixly is sinds 2014 ISO 27001-gecertificeerd. Dit betekent dat er volgens bepaalde richtlijnen met (strikt) vertrouwelijke informatie om wordt gegaan wat onder andere zorgt voor een veilige waarborging van de testresultaten. Alle gegevens worden anoniem en ‘encrypted’ opgeslagen in een (met SSL certificaten) afgeschermde database: deze database staat op een andere server dan waar de web-applicatie staat. Externe partijen (zoals software developers) werken met anonieme data, waardoor de privacy van kandidaten gewaarborgd is.

Verder houdt ISO 27001-certificatie in dat er jaarlijks een externe audit plaatsvindt, en er ieder kwartaal een risicoanalyse en continuïteitsplan gemaakt worden. Verder worden data-integriteit en beveiligingsincidenten continu bewaakt. Voor meer informatie over de inhoud van ISO 27001, zie http://searchsecurity.techtarget.co.uk/definition/ISO-27001.

[1] Op het moment van verschijnen van deze handleiding stond de website van Ixly op het punt geheel vernieuwd te worden. Vanaf 1 maart 2017 zullen de genoemde pagina’s te bezoeken zijn. Voor die tijd kan de informatie via http://www.test-toolkit.nl/handleiding-nieuwe-test-toolkit/ en http://www.test-toolkit.nl/veelgestelde-vragen/ te bezoeken – deze pagina’s zullen enige tijd daarna echter niet meer beschikbaar zijn.

[2] Het liefst hadden we dit empirisch aangetoond. Echter, van slechts een klein aantal gebruikers was op het moment van schrijven bekend of zij kandidaten thuis of in een testzaal lieten testen. Hierdoor waren de variabelen organisatie (waar de data van afkomstig waren), opleidingsniveau en testsituatie (proctored/unproctored) onvoldoende van elkaar te onderscheiden. In de toekomst is hier onderzoek naar gepland.

[3] De verificatietoets is geen onderdeel van deze handleiding. De methode die gehanteerd wordt is een Z-toets om de scores op de ACT Algemene Intelligentie en de scores op de verificatietoets te vergelijken (Guo & Drasgow, 2010). Uit simulatiestudies kwam deze methode als het meest accuraat naar voren (ook in eigen onderzoek met de ACT Algemene Intelligentie).

 

 

3. Handleiding voor testgebruikers

3.1 Inleiding

In dit hoofdstuk zal de toepassing, interpretatie en het gebruik van de ACT Algemene Intelligentie worden besproken. Er wordt ingegaan op de toepassingsmogelijkheden, de vereiste kennis voor de interpretatie van de testscores en de beperkingen van de test. De interpretaties van de testscores zullen aan de hand van enkele casussen verhelderd worden.

3.2. Toepassingsmogelijkheden

De ACT Algemene Intelligentie is in eerste instantie ontwikkeld voor selectiedoeleinden, maar kan in principe in elke situatie ingezet worden waarbij het van belang is om meer te weten te komen over iemands intellectuele vermogens. In lijn met het principiële doel van de test, is deze in eerste instantie bedoeld voor personen die deel uitmaken van de Nederlandse beroepsbevolking. De ACT Algemene Intelligentie geeft een beeld van iemands algemene intellectuele capaciteiten (de g-score), en meer specifiek van de numerieke (Cijferreeksen), figuratieve (Figurenreeksen) en verbale (Verbale Analogieën) capaciteiten van een persoon. Zodoende kan er een beeld gevormd worden over de geschiktheid van de kandidaat voor de betreffende functie.

Hoewel de ACT Algemene Intelligentie dus voornamelijk bedoeld is voor selectiedoeleinden, kan de test ook ingezet worden voor andere assessmentdoeleinden, zoals bij loopbaanvraagstukken waarbij een inschatting van het denkvermogen vereist is. Wanneer een persoon bijvoorbeeld vast zit in zijn/haar loopbaan, en met een loopbaancoach wil kijken wat de doorgroeimogelijkheden of bijscholingsmogelijkheden zijn, dan zal het intelligentieniveau bepaalde opties mogelijk maken of juist uitsluiten. In dit soort situaties zal de ACT Algemene Intelligentie ook een bruikbaar instrument zijn om inzicht te krijgen in het denkvermogen van de kandidaat. In sectie 3.6.3. worden twee casussen besproken waar hier in meer detail op ingegaan wordt.

3.3. Beperkingen van de test

De ACT Algemene Intelligentie is nog niet getoetst onder schoolpopulaties in de leeftijd van 15 jaar en jonger. Onderzoek zal moeten uitwijzen of de ACT Algemene Intelligentie ook toepasbaar kan zijn binnen deze doelgroep. Het zou een mooie aanvulling zijn als hier informatie over bekend wordt. Deze groepen vallen niet onder de doelgroep (beroepsbevolking), maar dit neemt niet weg dat de ACT Algemene Intelligentie mogelijk toepasbaar kan zijn binnen deze doelgroep.

3.4. Aanwijzingen voor de testleider

Alle informatie die de kandidaat nodig heeft om de test te kunnen maken staat beschreven in de instructie. Mocht de testleider vooraf al informatie willen verstrekken over het invullen van de test, dan kan het volgende gezegd worden:

• De test geeft een beeld van uw intellectuele capaciteiten. Met behulp van drie subtests worden uw numerieke, abstracte en verbale capaciteiten gemeten waarop uw algemene intelligentiescore gebaseerd is.
• De test duurt in totaal maximaal 40 minuten, maar meestal is de test eerder klaar.
• Voor iedere subtest verschijnt een uitleg met een voorbeeldvraag en oefenvragen.
• Voor elke vraag heeft u 45 seconden de tijd. Vul een antwoord in voordat de tijd verstreken is. Doet u dit niet, dan wordt de vraag fout gerekend.
• Wij raden aan de test in één keer af te ronden. Mocht u toch moeten onderbreken, dan kunt u na een subtest even onderbreken. Dit staat aangegeven op de betreffende schermen.
• Maak de test dus pas als u hier geruime tijd voor heeft, in ieder geval drie kwartier maar liever een uur.
• Maak de test in een rustige omgeving zodat u zich kunt concentreren.
• U mag kladpapier gebruiken bij de test.
• U kunt op F11 drukken voordat u de test begint om in een volledig scherm te werken. Druk weer op F11 om de volledig scherm stand weer af te sluiten.

Bij de geteste kandidaat moeten enkele basis computervaardigheden aanwezig zijn om de test te kunnen maken. De kandidaat moet:

1. In staat zijn om via de browser een internetpagina te kunnen vinden
2. In staat zijn om de gebruikersnaam en het wachtwoord in te voeren op de inlogpagina
3. In staat zijn om met gebruikmaking van de muis of het toetsenbord door de portal te navigeren (bijvoorbeeld op de starknop te klikken, de antwoordmogelijkheden aan te klikken en op volgende te klikken).

Voor mensen met een visuele beperking kunnen lettergrootte, contrast en kleuren worden aangepast met behulp van (standaard) browserinstellingen. De kandidaat kan er bovendien voor kiezen om de vragen alléén met behulp van een toetsenbord te maken, als het gebruik van een muis moeilijkheden oplevert.

Verder is er geen specifieke voorkennis of opleiding van de kandidaat vereist. Ook is het niet nodig dat kandidaten oefenen voordat ze de test gaan maken; dit kan natuurlijk wel. Ixly biedt niet specifiek voor de ACT Algemene Intelligentie oefen– of voorbeeldvragen aan. Op de website van Ixly staan echter wel verschillende voorbeeldtests die geraadpleegd kunnen worden door de kandidaten: dit laten wij echter over aan de kandidaten zelf of de adviseurs om de kandidaten hierop te attenderen. In de instructie, die de kandidaat leest voordat de subtests gemaakt wordt, krijgt hij/zij zoals hierboven beschreven een voorbeelditem en oefenopgaven te zien. Dus, op basis van de informatie van de testleider, de instructie van de test en de voorbeeld- en oefenopgaven heeft de kandidaat genoeg informatie om de test goed te kunnen maken.

3.5. Vereiste kennis voor het gebruik van de test

Als de ACT Algemene Intelligentie door een professional gebruikt wordt om anderen te adviseren of aan te nemen voor een functie, dan moet gegarandeerd worden dat:

• Diegene competent, gekwalificeerd, gelicentieerd of geautoriseerd is om psychologische tests te gebruiken voor de verschillende terreinen, zoals assessment, coaching, het geven van trainingen en Human Resource Management, waarin hij/zij werkzaam is. Eén en ander in overeenstemming met de in het land geldende wet- en regelgeving.
• Diegene zal handelen en gebruik maken van het product in overeenstemming met de nationale of internationale beroepsstandaarden en professionele ethiek.
• Diegene zal handelen en gebruik maken van het product in overeenstemming met de nationale of internationale wet- en regelgeving, instructies en richtlijnen en alle andere toepasselijke overheids- of semi-overheidsregels.
• Diegene het product enkel en alleen zal gebruiken voor de organisatie waar hij/zij werkzaam voor is of voor zijn/haar eigen bedrijf, in eigen naam en voor eigen rekening. Het is niet toegestaan het product te verkopen, leasen, kopiëren, geven, te overhandigen of over te dragen op welke manier dan ook aan welk bedrijf of persoon dan ook, behalve voor het gebruik van de producten en diensten als integraal onderdeel van de dienstverlening aan cliënten of voor gebruik binnen de organisatie die de directe werkgever van de professional is.

Ixly controleert de betrouwbaarheid en kennis van de professionals voordat er toegang verleend wordt tot de service of producten. Ixly behoudt zich het recht voor zonder opgaaf van reden iemand toegang te weigeren.

Hoewel de gebruiker niet gecertificeerd hoeft te zijn is het zeker aan te bevelen een training testinterpretatie bij Ixly te volgen voordat men de ACT Algemene Intelligentie professioneel gaat inzetten bij advies vraagstukken. Deze trainingen worden ongeveer eens per kwartaal aangeboden door Ixly. Tijdens deze training komen onder andere relevante theorieën over intelligentie en persoonlijkheid aan bod, wordt er ingegaan op de constructie en de structuur van de belangrijkste tests van Ixly en wordt er aandacht geschonken aan de interpretatie van de resultaten.

3.6. Interpretatie scores

3.6.1. Berekening subtestscores en g-score

Hoe de θ’s van de subtests tot stand komen is uiteengezet in Hoofdstuk 1: we gebruiken de EAP-methode om θ te berekenen. Op basis van deze scores kunnen de scores voor de drie subtests teruggekoppeld worden.

Hoewel deze specifieke scores interessant zijn, zal men in de praktijk vooral gebruik willen maken van de g­-score, mede door het voorspellend vermogen wat betreft werkgerelateerde uitkomsten zoals werkprestatie (Schmidt & Hunter, 1998). Deze g-score wordt berekend door een gewogen gemiddelde te nemen van de drie θ-scores op basis van de subtests: de weging vindt plaats op basis van de betrouwbaarheid van de subtestscores. Het idee hierachter is dat minder betrouwbare metingen (subtestscores) ook minder gewicht krijgen  in de berekening van g: dit zal de meest betrouwbare meting van g opleveren. De SEM (standaardfout) van de g-score wordt berekend door de informatie (= 1/SEM²) geleverd door de drie subtests op te tellen en hiermee weer de SEM te berekenen (= 1/√Info).

Deze berekeningen veronderstellen overigens dat de drie subtests tot hetzelfde domein behoren: dat wil zeggen dat ze alle drie een meting van hetzelfde construct zijn. Mocht dit niet het geval zijn dan zouden de informatiewaarden niet zomaar gesommeerd mogen worden. De intercorrelaties tussen de subtests en het feit dat deze door één factor verklaard kunnen worden bevestigt deze veronderstelling (zie Hoofdstuk 6).

3.6.2. Terugkoppeling van scores

De scores op de ACT Algemene Intelligentie worden teruggekoppeld aan de hand van een viertal maten: stenscore, T-score, percentielscore en IQ-scores (numeriek, abstract, verbaal en totaal). Het grote voordeel van θ is dat dit een normaal verdeelde score is. Deze is dus eenvoudig om te rekenen naar andere standaardscores. Standaardscores geven een beeld van hoe een bepaalde score zich verhoudt tot het gemiddelde van alle scores in een bepaalde referentiegroep: een ‘gemiddelde’ score is dus een score die in de referentiegroep veel voorkomt, terwijl een erg hoge (of lage) score betekent dat deze weinig voorkomt in de referentiegroep. Als referentiegroepen hanteren we de opleidingsniveaus VMBO, MBO, HBO en WO voor de stenscores, T-scores en percentielscores, en een referentiegroep beroepsbevolking voor de IQ-score (zie Hoofdstuk 4). Voor de stenscores en de IQ-scores wordt de SEM gebruikt om het 80% betrouwbaarheidsinterval aan te duiden, grafisch of in tekst (“We kunnen met 80% zekerheid zeggen dat uw totaalscore ligt tussen X en Y”).

De vier ruwe scores van de ACT Algemene Intelligentie, dat wil zeggen de θ-scores op de subtests Cijferreeksen, Figurenreeksen en Verbale Analogieën en de g-score, worden eerst omgerekend naar een Z-score en vervolgens naar de stenscore, T-score en percentielscore met behulp van de gemiddelde en standaarddeviaties van de vier normgroepen naar opleidingsniveau (zie Hoofdstuk 4). De IQ-score wordt berekend met behulp van het gemiddelde en de standaarddeviatie van de beroepsbevolking referentiegroep.

De adviseur kan een uitgebreid rapport opvragen waarbij zelf voor vergelijkingen met één of meer normgroepen gekozen kan worden. Standaard wordt alleen een rapport getoond met de IQ-scores voor het numerieke, abstracte en verbale gedeelte en voor het totaal. Er is ook een rapport beschikbaar zonder deze IQ-scores, en met dus alleen maar vergelijkingen met de normgroepen op basis van opleidingsniveau. Zie voor een voorbeeldrapport Bijlage 3.1.

3.6.2.1. Stenscore

Deze schaal loopt van 1 tot 10. Stenscores zijn een vorm van standaardscores met een gemiddelde van 5.5 en een standaarddeviatie van 2. Stenscores geven een beeld van hoe een bepaalde score zich verhoudt tot het gemiddelde van alle scores. Stenscore 4, 5, 6 en 7 liggen allemaal binnen 1 standaarddeviatie van het gemiddelde. Stenscore 2, 3 en 8, 9 liggen tussen 1 en 2 standaarddeviatie van het gemiddelde. Stenscore 1 en 10 liggen meer dan 2 standaarddeviaties van het gemiddelde. De gemiddelde score in de normgroep ligt precies op de grens van de vijfde en zesde sten. Hierbij moet opgemerkt worden dat stenscores niet verward moeten worden met schoolcijfers. Een stenscore van bijvoorbeeld 5 is niet een onvoldoende, maar betekent een ‘gemiddelde’ score die in de referentiegroep veel voorkomt. De percentages die horen bij de afzonderlijke stenscores zijn als volgt:

Tabel 3.1. Stenscores met bijbehorende percentages.
Sten	Percentage	Cumulatieve   percentage
1	2.3%	2.3%
2	4.4%	6.7%
3	9.2%	15.9%
4	15%	30.9%
5	19.1%	50.0%
6	19.1%	69.1%
7	15%	84.1%
8	9.2%	93.3%
9	4.4%	97.7%
10	2.3%	100%

 

3.6.2.2. T-score

Deze schaal loopt van 0-100. Ook T-scores zijn een vorm van standaardscores. T-scores hebben een gemiddelde van 50 en een standaarddeviatie van 10. Binnen een normale verdeling kan gesteld worden dat 99,74% van alle scores binnen T-scores van 20 tot 80 vallen aangezien deze scores 3 standaarddeviaties boven of 3 standaarddeviaties onder het gemiddelde liggen.

3.6.2.3. Percentielscore

Een percentielscore refereert naar de proportie mensen in de referentiegroep wiens score lager dan of gelijk aan een bepaalde testscore was. Dus: als 15 procent van de personen in de normgroep een (ruwe) score van 20 of lager heeft behaald, dan wordt gesteld dat de (ruwe) score 20 een percentielscore van 15 heeft. Bij de interpretatie van percentielscores dient men te onthouden dat hoe hoger de percentielscore is hoe hoger de score van de betreffende persoon, ten opzichte van anderen.

Percentielen zijn niet evenredig verdeeld over een normale verdeling. Binnen een normaalverdeling is het grootste deel van de personen gecentreerd rond het midden. Personen met een extreem hoge of extreem lage score zijn er relatief weinig. De afstand tussen het 1^e en 2^e percentiel is om die reden veel groter dan de afstand tussen (bijvoorbeeld) het 5^e en 6^e percentiel.

3.6.2.4. IQ-score

De resultaten op de ACT Algemene Intelligentie worden ook teruggekoppeld als IQ-score. De IQ-score is ook een standaardscore met een gemiddelde van 100 en een standaardafwijking van 15 (IQ = (Z * 15) + 100).

3.6.2.5. Rekenvoorbeeld

Om verder inzicht te geven in de gehanteerde scores volgt hier een rekenvoorbeeld. Iemand heeft een ‘ruwe’ g-score van 0.5 gehaald. De bijbehorende stenscore vergeleken met de VMBO-referentiegroep van deze persoon is 8.3. Deze score is als volgt berekend. Eerst wordt de Z-score berekend met de volgende formule:

(3.1)

Hierin is X de behaalde ruwe score, μ is het groepsgemiddelde, en σ de standaarddeviatie van de scoreverdeling. De gemiddelde g-score voor de VMBO-groep is -0.24, de standaarddeviatie is .53 (zie Hoofdstuk 4). De Z-score van deze persoon is dus (0.5 – -0.24)/0.53 = 1.40. Omgerekend naar een stenscore is dit 5.5 + 2 * 1.40 = 8.3. De bijbehorende T-score is 50 + (10 * 1.40) = 64 en percentielscore is 92. Vergeleken met de VMBO-referentiegroep scoort deze persoon dus hoger dan gemiddeld.

Vergeleken met de WO-groep is de Z-score (0.5 – 0.83)/0.50 = -0.66. In stenscores uitgedrukt heeft deze persoon een score van 4.2 gehaald. De bijbehorende T-score is 50 + (10 * -0.66) = 43.4 en percentielscore is 25. Vergeleken met de WO-referentiegroep scoort deze persoon dus lager dan gemiddeld. Meer informatie hierover is te vinden in Hoofdstuk 4 en in de normtabellen (Bijlagen 4.1. en 4.2.).

De IQ-score zegt iets over de score van een persoon vergeleken met de totale normpopulatie (Nederlandse beroepsbevolking). Om de IQ-score te berekenen wordt eerst de Z-score verkregen door van de ruwe θ het gemiddelde van de totale normgroep af te trekken en te delen door de standaarddeviatie van de scores in deze groep (zie Hoofdstuk 4). De gemiddelde g-score van de totale normgroep is 0.17 en de standaarddeviatie is 0.71. De Z-score van deze persoon is dus (0.5 –0.17)/0.71 = 0.46. De behaalde IQ-score is dus 100 + (0.46 * 15) = 106.9.

3.6.3. Interpretatie van de scores in een selectie- en adviessituatie

Om de interpretatie van de WPV Compact te illustreren hebben twee psychologen door middel van twee casussen toegelicht hoe zij de ACT Algemene Intelligentie toepassen bij zowel een selectie- als adviessituatie. Hoewel de ACT Algemene Intelligentie primair voor selectievraagstukken is ontwikkeld is deze ook inzetbaar bij adviessituaties waarbij het van belang is inzicht te krijgen in het denkvermogen van een persoon. Daarom worden voor beide situaties casussen toegelicht.

De ACT Algemene Intelligentie kan zelfstandig ingezet worden, maar het is gebruikelijker om meerdere vragenlijsten in te zetten: zo kan een breed beeld gevormd worden over wie de persoon is, wat hij/zij interessant en motiverend vindt in een baan en wat hij/zij kan (door middel van de ACT Algemene Intelligentie). Daarom wordt in onderstaande casussen ingegaan op de resultaten van de ACT Algemene Intelligentie in combinatie met andere vragenlijsten van Ixly.

3.6.3.1. Casus selectie

Functieomschrijving

Een opleidingsinstituut met specialisatie in de sector transport is op zoek naar nieuwe chauffeurs voor een leer/werk-traject. De functie is als volgt beschreven:

Als je vrachtwagenchauffeur bent, heb je geen standaard baan. Het werk en de werkgevers vragen veel van je. We hebben daarom een profiel gemaakt van mensen die we zoeken. Herken jij je in deze eigenschappen? Je bent:

• Echt gemotiveerd om chauffeur te worden.
• Flexibel inzetbaar.
• Klantvriendelijk en stressbestendig.
• Zelfstandig en communicatief vaardig.
• Iemand die zich goed kan aanpassen aan verschillende situaties.
• Lichamelijk fit.
• Bereid om aan te pakken, een chauffeur ben je niet van 9 tot 5.

Naast de hierboven genoemde eigenschappen is het belangrijk dat de toekomstige chauffeurs een goed begrip van de Nederlandse taal hebben (minimaal B1 taalniveau op een begrijpend lezen test) en minimaal in het bezit zijn van een vmbo-diploma en/of mbo werk- en denkniveau. Om te bekijken of de sollicitanten aan deze eisen voldoen wordt een assessment afgenomen tijdens een testdag. Dit assessment bestaat uit de ACT Algemene Intelligentie (mbo werk- en denkniveau), een persoonlijkheidstest (o.a. flexibiliteit, communicatieve vaardigheid en zelfstandigheid), een taaltest (begrip van Nederlandse taal) en een reactietijdentest. Deze laatste test is van belang aangezien de chauffeurs gedurende lange tijd alert moeten blijven.

In deze casus bespreken we de resultaten van twee kandidaten: Pieter en Joost.

Pieter

Pieter is 27 en heeft enkele jaren geleden de mbo-2 opleiding Stand- en decorbouwer afgerond. Hij heeft enkele jaren gewerkt bij verschillende bedrijven, steeds met korte contracten maar tot een vast contract is het nooit gekomen. Hij is nu op zoek naar wat meer stabiliteit en wil daarom een overstap maken.

Joost

Joost is 21 en is vorig jaar gestopt met zijn opleiding Infratechniek. Hij vond de opleiding en het werkveld teveel gericht op details en planningen. Hij werkt momenteel als orderpicker maar heeft, na enkele gesprekken met collega’s, interesse in de opleiding tot vrachtwagenchauffeur.

Hieronder zijn in verschillende grafieken de resultaten van beide kandidaten weergegeven. Hun resultaten worden per onderdeel besproken en aan het einde wordt besloten of de kandidaat verder gaat in het proces.

 Resultaten

 Hieronder worden eerst de resultaten van de persoonlijkheidstest getoond in de vorm van competentiescores. Vervolgens worden per kandidaat de scores voor diverse vaardigheden getoond. Deze uitslagen worden besproken, waarbij met name dieper ingegaan wordt op de uitslag van de ACT Algemene Intelligentie.

 Figuur 3.1. Competenties Pieter.
                                           

 

Figuur 3.2. Competenties Joost.

In Figuur 3.1. en 3.2. is te zien dat zowel Pieter als Joost qua competenties goed passen bij het bedrijf. Joost scoort op de meeste competenties iets hoger dan Pieter. Echter in het geval van de competentie Verantwoordelijkheid is een hoge score niet per definitie positief. Over het algemeen blijkt uit de test dat zowel Pieter als Joost in ruim voldoende mate de competenties hebben die nodig zijn voor deze functie en dat zij dus goed om zullen kunnen gaan met de uitdagingen van het werk.

 Tijdens de nabespreking geven beiden aan zich wel te herkennen in hun scores. Zo geeft Pieter aan dat hij bij zijn vorige werkgevers regelmatig met suggesties kwam tijdens de uitvoering van een project. Hij vond het soms jammer dat er enkel werd verwacht dat hij instructies uitvoerde, terwijl hij graag mee wilde denken om dingen te verbeteren. Dit sluit aan bij zijn hoge scores op ‘zelfstandig oordelen’ en ‘verantwoordelijkheid’.

Joost is enigszins verbaasd over zijn hoge scores op de competenties en vooral over het feit dat zijn hoge score op verantwoordelijkheid in het gele gedeelte van de grafiek valt. Maar tijdens de nabespreking komen er toch wel enkele verhalen naar voren, waardoor hij de aansluiting met de scores wel ziet. Tijdens zijn studie nam hij bijvoorbeeld vaak de leiding tijdens groepsprojecten. Hoewel hij deze leidende rol leuk vond was het voor hem soms ook lastig om zijn groepsgenoten los te laten. Hij wilde graag een goed resultaat afleveren en had de neiging alles te controleren of naar zich toe te trekken. Gezien deze valkuil is de score op ‘verantwoordelijkheid’ uiteindelijk toch herkenbaar.                                                        

Figuur 3.3. Vaardigheden Pieter.

Figuur 3.4. Vaardigheden Joost.

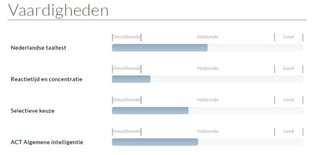
 Wanneer we kijken naar de verschillende vaardigheden in Figuur 3.3. en 3.4. zien we in eerste instantie ook niet veel verschillen tussen de twee kandidaten. Op de Nederlandse taaltest scoren beiden vrijwel gelijk. Hun taalniveau is dus goed genoeg om de opleiding en het werk aan te kunnen.
Op een simpele reactietijdentaak scoren beide kandidaten niet heel sterk. Pieter scoort net op de grens van onvoldoende naar voldoende, terwijl Joost net iets boven die grens scoort.
De meer gedetailleerde uitslagen (hier niet weergegeven) laten zien dat beiden een vrij gemiddelde reactietijd hebben, maar dat ze vrij veel fouten maken. Dit wil zeggen dat ze regelmatig te vroeg hebben gereageerd of een stimulus niet op tijd hebben gezien. Oftewel: Beide deelnemers reageren normaal wanneer zij een stimulus herkennen, het komt echter regelmatig voor dat zij een stimulus over het hoofd hebben gezien of ten onrechte denken een stimulus gezien te hebben.

Op de selectieve keuze reactietijdentest zien we dat Joost hoger scoort dan Pieter. Ook hier zien we weer dat Pieter vrij veel fouten maakt. Zijn prestatie is echter wel stabieler dan die van Joost, die gemiddeld goede, maar vrij wisselende, reactietijden laat zien.

Het grote verschil tussen de twee deelnemers ontstaat wanneer we kijken naar de ACT Algemene Intelligentie. Pieter scoort hier weer net op de grens van onvoldoende naar voldoende, terwijl Joost ruim voldoende scoort.

Pieter scoort vergeleken met de MBO-normgroep beneden gemiddeld terwijl Joost rondom het gemiddelde voor deze normgroep scoort. Aangezien er minimaal een mbo werk- en denkniveau gevraagd wordt voor de functie is de score van Pieter dus te laag.

 
Figuur 3.5. Details ACT Algemene Intelligentie Pieter

 

 

Figuur 3.6. Details ACT Algemene Intelligentie Joost

Wanneer gekeken wordt naar de scores per subtest (Figuur 3.5. en 3.6.) is te zien dat de score op Figurenreeksen, die het abstracte redeneervermogen meet, voor beiden ongeveer gelijk ligt. Beide kandidaten scoren hier naar verwachting voor iemand met mbo werk- en denkniveau. Deze subtest meet het duidelijkst de fluid intelligentie van een persoon. Ook de subtest Cijferreeksen meet voornamelijk de fluid intelligentie, al wordt er voor Cijferreeksen wel verondersteld dat men basiskennis bezit wat betreft rekenen.

Wanneer we kijken naar de scores van Pieter valt op dat hij aanzienlijk lager op de subtest Cijferreeksen scoort dan op de subtest Figurenreeksen. Dit soort verschillen kunnen in de praktijk voorkomen. Uit eerder onderzoek blijkt dat de subschalen van de ACT Algemene Intelligentie een correlatie hebben van ongeveer .60 (zie Hoofdstuk 6). Over het algemeen wordt dus gezien dat iemand die hoog scoort op de ene subtest ook hoog scoort op de anderen. Echter zullen er ook kandidaten zijn die op een bepaalde subtest hoger of juist lager scoren, zoals Pieter. Hier kunnen verschillende verklaringen voor zijn zoals een gebrek aan basisvaardigheden of dyscalculie.

Tijdens een nabespreking kunnen dit soort verschillen en de mogelijke oorzaken daarvoor eventueel besproken worden met de kandidaat. Voor een interpretatie van de scores is het vooral belangrijk om te kijken naar de algemene trend van de scores. In het geval van Pieter zien we één subtest waarbij hij gemiddeld scoort en twee subtests waar hij benedengemiddeld scoort. Bij Joost is de interpretatie van de scores gemakkelijker aangezien hier een relatief stabiel scorepatroon te zien is, waarbij alle scores rondom het gemiddelde zitten.

De score van Pieter op de subtest Verbale Analogieën is opnieuw benedengemiddeld. De subtest Verbale Analogieën verondersteld van alle subtests de meeste voorkennis. Dit wil niet zeggen dat deze test enkel crystallized intelligentie meet. De items zijn zo ontworpen dat de meeste deelnemers de gebruikte woorden zullen kennen. De moeilijkheid van de items ligt hem vooral in het ontdekken van de complexere relaties en patronen. Er kan dan ook niet zomaar geconcludeerd worden dat een lagere score op deze specifieke subtest een teken is van een lager taalniveau.

Dat is dan ook in dit geval te zien. Pieter scoort voldoende op de Nederlandse Taaltest, maar beneden gemiddeld op Verbale Analogieën. Joost heeft een vergelijkbare score met Pieter op de Nederlandse taaltest, maar scoort wel gemiddeld op Verbale Analogieën. Hieruit is te concluderen dat de benedengemiddelde score van Pieter vooral een weerspiegeling is van het verbale redeneervermogen en dat zijn taalniveau de beneden gemiddelde score niet volledig kan verklaren.

Tijdens de nabespreking reageert Pieter teleurgesteld op zijn scores. Hij geeft aan dat hij erg nerveus was voor de assessmentdag. Op school en tijdens zijn studie had hij veel moeite met schriftelijke toetsen waarvoor hij ook altijd zenuwachtig was, terwijl hij bij praktijkopdrachten wel goed presteerde. Hij omschrijft zichzelf dan ook als ‘een praktijkman’. Hij kan niet verklaren waarom hij met name op de subtest Cijferreeksen een lage score had behaald, behalve dat hij wiskunde altijd een van de lastigste vakken vond op school.

Joost is tevreden over zijn scores, hij had tijdens de assessmentdag al wel een goed gevoel over de tests. De scores op de reactietijdtests valt hem als enige wat tegen. Als verklaring hiervoor noemt hij dat dit de laatste tests waren van de dag en dat de dag langer duurde dan hij had verwacht. Aangezien hij die avond nog een afspraak had, maakte hij zich zorgen of hij wel op tijd thuis zou zijn en merkte hij dat hij moeite had om er goed bij te blijven.

Conclusie

Pieter wordt, ondanks het feit dat hij qua persoonlijkheid goed past bij de functie, afgewezen als chauffeur. Zijn scores op de reactietijdentests bevatten te veel fouten, wat gevaarlijke situaties op zou kunnen leveren. Uit de ACT Algemene Intelligentie blijkt bovendien dat hij niet beschikt over mbo werk- en denkniveau. Hierdoor bestaat het risico dat de opleiding te zwaar voor hem is, waardoor hij deze mogelijk niet af zal kunnen ronden.

Joost wordt wel aangenomen als chauffeur. Zijn prestatie op de Reactietijd- en concentratietest was aan de lage kant, maar wel voldoende. Bovendien laten zijn ACT Algemene Intelligentie scores zien dat zijn denkniveau voldoende is om de opleiding succesvol af te kunnen ronden.

3.6.3.2. Casus advies

Introductie

Om inzicht te geven in de interpretatie van de testresultaten van de ACT Algemene Intelligentie bij loopbaanvragen, bespreken we hieronder een casus voor loopbaanbegeleiding. In de praktijk wordt de ACT Algemene Intelligentie binnen loopbaanbegeleiding vaak afgenomen samen met de Werkgerelateerde Persoonlijkheidsvragenlijst, Werkwaarden en Vragenlijst voor Interesse in Taken en Sectoren, om naast denkniveau een beeld te krijgen van de persoonlijkheidseigenschappen, drijfveren en interesses van de persoon. Afhankelijk van de onderzoeksvraag kan de ACT Algemene Intelligentie afzonderlijk of in combinatie met deze vragenlijsten ingezet worden.

Situatieschets

Pim Kuijpers is een jongeman van 23 jaar. Na vmbo-advies te hebben ontvangen op de basisschool is hij vmbo theoretische leerweg gaan volgen. Het eerste jaar had hij moeite met de andere manier van leren; de verschillende vakken naast elkaar en de toetsweken aan het eind van iedere periode vond hij zwaar. Hij voelde zich op zijn plek op het vmbo en ontdekte zijn interesse in economie. Hij was gemotiveerd en heeft met een 7,3 gemiddeld zijn vmbo-diploma behaald en is doorgestroomd naar 4-havo. Al snel merkte hij dat hij het moeilijk vond de grote hoeveelheid stof te leren voor de tentamens en het huiswerk bij te houden. Na een half jaar is hij overspannen geraakt en heeft hij het schooljaar niet af kunnen maken. In 2013 is hij met de mbo-opleiding Financieel dienstverlener begonnen. Na zijn opleiding te hebben voltooid is hij gaan werken bij het verzekeringsbedrijf waar hij zijn afstudeerstage heeft gevolgd. Momenteel werkt hij als financieel dienstverlener bij dit verzekeringsbedrijf.

Vraagstelling

Pim merkt dat de uitdaging in zijn werk minder wordt en hij graag verder zou doorstuderen om verder te kunnen groeien in het bedrijf en bijvoorbeeld als financieel adviseur te kunnen gaan werken. Hij overweegt de hbo opleiding Financiële Dienstverlening, maar vraagt zich af of dit wel aansluit en of hij dit aan zou kunnen.

De volgende tests  en vragenlijsten zijn afgenomen om de vraag te beantwoorden:

• Werkgerelateerde Persoonlijkheidsvragenlijst – Normatief (WPVN)
• Carrière Waarden – Ipsatief (CWI)
• Vragenlijst voor Interesse in Taken en Sectoren (ITS)
• ACT Algemene Intelligentie

Testresultaat

ACT Algemene Intelligentie

Om de algemene intelligentie te bepalen is de ACT Algemene Intelligentie ingezet. De resultaten staan weergegeven in Figuur 3.7.

Figuur 3.7. Resultaten ACT Algemene Intelligentie Pim.

De ACT Algemene Intelligentie geeft een indicatie van de IQ-score met het betrouwbaarheidsinterval per subtest en totaal. Daarnaast is voor de huidige casus de stenscore in vergelijking met de referentiegroep mbo en hbo/bachelor opgevraagd.

De IQ-score als algemene maat van intelligentie geeft een gemiddelde score (score van 100) wat duidt op een gemiddelde intelligentie. Als gekeken wordt naar de IQ-score per subtest voor de subtest Abstract (Figurenreeksen) en Verbaal (Verbale Analogieën) valt op dat de scores eveneens duiden op een gemiddeld abstract en verbaal denkvermogen. Bij de numerieke subtest (Cijferreeksen) in relatie tot de andere subtests kan gezegd worden dat de kandidaat wat minder sterk is in cijfermatig analytisch vermogen dan in abstract en verbaal denkvermogen. De IQ-score bij de numerieke subtest ligt alleen net iets beneden het gemiddelde.

Als de scores vergeleken worden met de mbo referentiegroep ligt de totaalscore rond het gemiddelde. Wat wil zeggen dat de algemene intelligentie van Pim overeenkomt met mbo denkniveau. Ook hier wordt duidelijk dat Pim op abstract en verbaal redeneervermogen gemiddeld scoort en numeriek beneden gemiddeld. In vergelijking met de hbo normgroep ligt de algemene intelligentie beneden gemiddeld. In vergelijking met de hbo normgroep scoort Pim net beneden gemiddeld op abstract en verbaal redeneervermogen en voor het cijfermatig redeneervermogen ruim beneden gemiddeld.

In de bespreking geeft Pim aan het toch confronterend te vinden, maar wel te herkennen. Zo geeft hij aan de mbo-opleiding goed aan te kunnen, maar op de havo erg hard te moeten werken om bij te kunnen blijven. De numerieke subtest had hij, aldus Pim, ook echt moeite mee, de verbale subtest ging hem gemakkelijker af.

Samenvattend komt uit de ACT Algemene Intelligentie naar voren dat Pim over een gemiddelde mate van intelligentie lijkt te beschikken. Vergeleken met hbo en mbo referentiegroepen geeft de ACT Algemene Intelligentie een mbo denkniveau aan, waarbij Pim in conceptueel en verbaal denkvermogen wat sterker is dan in cijfermatig denkvermogen.

Persoonlijkheid

De Werkgerelateerde Persoonlijkheidsvragenlijst rapporteert op vijf factoren die ieder bestaan uit een aantal schalen, zie Figuur 3.8.

Figuur 3.8. Resultaten WPVN Pim.

Als gekeken wordt naar het volledige persoonlijkheidsprofiel dan blijkt hieruit een gevarieerd scoreprofiel met duidelijk uitgesproken scores en minder uitgesproken scores. De score op de factor Invloed (3) geeft een beneden gemiddelde score, met name gedreven door een lagere score op Status (2) en Zelfvertoon (2). Een hoge positie bekleden en aandacht naar zich toe trekken zijn persoonlijkheidskenmerken die minder aanwezig zijn bij Pim. De lagere score op Sociabiliteit (3) komt voornamelijk naar voren door een beneden gemiddelde score op Contactbehoefte (3), Sociaal ontspannen (3) en Zelfonthulling (3). Dit duidt op een mindere behoefte aan contact, verlegenheid in sociale situaties en terughoudendheid in het delen van gevoelens. Verder zien we een hoge score op Structuur (8) wat wil zeggen dat hij redelijk ordelijk en gestructureerd is, waarbij vooral Nauwkeurigheid (10)  een dominante persoonlijkheidstrek blijkt. Daarnaast geeft Regelmaat (8) een voorkeur voor regels en procedures aan. Gedrevenheid (5) is gemiddeld, met scores rond het gemiddelde op de schalen Energie (6), Zelfontwikkeling (4), Volharding (6), Originaliteit (4), Onafhankelijkheid (6). Dit duidt op een gemiddelde hoeveelheid energie en doorzettingsvermogen. Hij heeft wat minder vermogen om zich aan te passen aan veranderingen, wat zichtbaar is in de score op Vernieuwing (3). De score op emotionele stabiliteit ligt aan de bovenkant van het gemiddelde (Stabiliteit (6)). Hij heeft een gemiddelde mate van Zelfvertrouwen (5) en Positivisme (5). Meest prominent is dat hij gemakkelijk om kan gaan met kritiek (Incasseringsvermogen (8)) en geduldig is (Frustratietolerantie (7)).

Figuur 3.9. Resultaten Competentie-Indicator Pim.

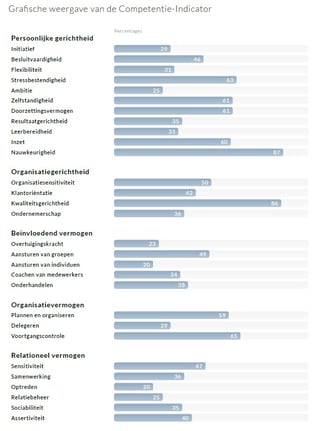
Op basis van het persoonlijkheidsprofiel komen met name kwaliteitsgerichtheid en nauwkeurigheid als makkelijk te ontwikkelen competenties naar voren. In mindere mate liggen zijn talenten ook bij de competenties voortgangscontrole, stressbestendigheid, zelfstandigheid, doorzettingsvermogen, inzet en plannen en organiseren.

Over het algemeen wordt het persoonlijkheidsprofiel herkend door Pim. Hij kreeg inderdaad in zijn functioneringsgesprek ook de nadruk op kwaliteit en zijn nauwkeurige manier van werken terug. Hij vindt dit ook duidelijke karakteristieken van zichzelf. Op zijn werk houdt hij ervan zijn werk volgens de voorschriften uit te voeren en heeft hij moeite met een nieuwe werkwijze die net geïntroduceerd is. Op doorzettingsvermogen had hij een hogere score verwacht. Hij geeft aan juist op de havo door te zijn gegaan tot het niet meer kon.

Werkwaarden

Met de werkwaarden vragenlijst zijn de primaire motivatoren (de belangrijkste werkwaarden), secundaire motivatoren, neutrale motivatoren en demotivatoren (werkwaarden die demotiverend zijn) vast te stellen. Deze kunnen opgevraagd worden in het rapport of afgelezen worden uit de grafische weergave van de werkwaarden die geclusterd zijn in Opbrengsten, Activiteiten en Omgeving (zie Figuur 3.10.).

Figuur 3.10. Resultaten CWI Pim.

Er blijkt sprake van een balans tussen de energie die hij haalt uit privé en uit werk. De belangrijkste werkwaarden voor Pim zijn Dynamiek (8) en Kwaliteit (8). In zijn huidige werk komt deze dynamiek ook terug door de diversiteit in klantopdrachten en is het juist van belang kwaliteit te leveren. Ook belangrijk zijn Financiële beloning (7), Autonomie (7) Zekerheid en Stabiliteit (7), Concrete resultaten (6), Carrière (6) en Ondernemen (6) . Pim herkent dat hij graag weet waar hij aan toe is, zo heeft hij nu een duidelijk takenpakket en duidelijke afspraken over wanneer welke taken gedaan moeten worden. In zijn huidige baan mist Pim wat meer autonomie en wat meer eigen verantwoordelijkheden. Hij wil ook verder in zijn carrière.  Dit zijn ook redenen waarom hij verder wil studeren om een hogere functie te kunnen gaan bekleden. Demotiverend voor hem zijn Samenwerking (4), Taakuitdaging (4), Beïnvloeden (4), Creatief denken (4), Waardering en erkenning (4) en Ontwikkelen (3). Hij heeft niet echt de behoefte om binnen het team invloed uit te oefenen, hij houdt er meer van dat binnen het werk ieder zijn eigen klantopdrachten toebedeeld krijgt en iedereen zijn of haar taken uitvoert. De mogelijkheid om zich verder te ontwikkelen of nieuwe taken te gaan uitvoeren is voor Pim niet belangrijk.

Vragenlijst voor Interesse in Taken en Sectoren

Deze vragenlijst geeft een grafische en tekstuele weergave van de interessegebieden, interesse in sectoren en taken geordend van hoog naar laag. Zie Figuur 3.11.

Figuur 3.11. Resultaten ITS Pim.

Uit de ITS komt met name een interesse naar voren in de sectoren Administratie (7) en Commerciële dienstverlening (6). Pim heeft een duidelijke voorkeur voor deze sectoren, in de andere sectoren zoals Welzijn, Veiligheid, Rechtspraak en Onderwijs, training en instructie ligt beduidend minder zijn interesse. Deze interesse sluit aan bij zijn huidige beroep, dat zich in het snijvlak van deze sectoren bevindt. Andere beroeps- en opleidingsmogelijkheden binnen deze sectoren kunnen bekeken worden.

De taken die hij leuk vindt vallen onder verschillende taakgebieden. De taken die hem het meest interesseren blijken Rekenen (5) en Met computers werken (5). Daarnaast komt Creatief zijn (3) naar voren en enkele ondersteunende taken, zoals Administratieve taken (4) en Werkzaamheden plannen (4). Eveneens in mindere mate interesseert hij zich voor sociale taken die passen bij commerciële dienstverlening; Assisteren (4), Met collega’s overleggen (4), Mensen begeleiden (4), Mensen overtuigen (4) en Contact onderhouden (4). Deze taken sluiten aan bij zijn huidige beroep.

Inderdaad trekt werken in de commerciële dienstverlening hem al sinds zijn studie. Zijn studie heeft hij gekozen, omdat hij het werken bij een commercieel bedrijf interessant vond, ook al wist hij wel dat werken als verkoper niets voor hem was. In zijn werk ziet hij ook terug dat hij het narekenen van schadeclaims en uitrekenen van bepaalde vergoedingen graag doet. Op de middelbare school vond hij juist van economie het maken van berekeningen leuk. Creatief bezig willen zijn herkent hij minder, hij is wel iemand die op de afdeling meehelpt oplossingen te bedenken bij klantproblemen, maar hoeft niet echt creatief te zijn in zijn werk. Hij vindt het juist leuk om zijn werk te doen voor de klanten, maar meer indirect contact te hebben met de klant.

Conclusie en advies

Samenvattend is Pim iemand die geordend en gestructureerd werkt, met een goed oog voor details, en die het prettig vindt regels en procedures te volgen. Hij is geduldig, kan gemakkelijk omgaan met kritiek en is wat terughoudend en verlegen in sociaal contact. Hij blijkt over een redelijke mate van doorzettingsvermogen, energie en zelfvertrouwen te beschikken wat hem zou helpen de inzet op te brengen om een hbo-opleiding te volgen. De opleiding Financiële Dienstverlening komt overeen met zijn interesses en sluit aan bij het werkveld waarin hij nu werkt en verder in door zou willen groeien. Hij lijkt een mbo-denkniveau te hebben, wat wil zeggen dat het denkniveau minder aansluit bij het denkniveau wat binnen een hbo-opleiding gevraagd wordt. Een hbo-opleiding zou veel extra inspanning van hem vragen en is daarom minder geschikt. Zijn huidige werk is gestructureerd waarin de nadruk wordt gelegd op kwaliteit, wat goed aansluit op wat Pim zoekt in zijn werk en zijn kwaliteitsgerichtheid. Doorgroeien binnen zijn bedrijf zou hem de kans geven zijn baan meer te laten aansluiten op de andere werkwaarden die voor hem belangrijk zijn, zoals verder werken aan zijn carrière, meer autonomie en eigen verantwoordelijkheden.

Het advies op basis van de resultaten is dat een hbo-opleiding minder passend is, en dat meer gekeken kan worden naar groeimogelijkheden binnen het bedrijf of binnen de financiële dienstverleningssector.

Het bespreken van het advies vond Pim moeilijk. Hij ziet wel in dat het niveau te hoog kan zijn, omdat hij ook op de havo merkte dat hoe hard hij ook werkte, het niet genoeg leek te zijn. Maar hij vindt het lastig dit toch te accepteren.

Epiloog

Pim heeft zijn werk opgezegd en is in september gestart met de hbo-opleiding Financiële Dienstverlening. Na een paar maanden is hij in overleg met de studieadviseur gestopt met de opleiding en weer teruggekeerd naar zijn werkgever.

3.6.4. Relevante informatie bij de interpretatie

Selectieprocedures brengen voor kandidaten altijd spanningen met zich mee; sommigen zullen hier goed tegen kunnen, terwijl dit voor anderen een groter probleem is. Het kan zijn dat mensen hierdoor wat lager presteren dan verwacht. Ook kan het zijn dat iemand bijvoorbeeld last heeft van faalangst, of dat hij/zij technische problemen met de computer had tijdens het maken van de test, wat de testscores beïnvloed zal hebben. Om inzicht te krijgen in dit soort omstandigheden kunnen tests onzes inziens nooit geïnterpreteerd worden zonder een interview. De waarde van deze test is vooral gelegen in het feit dat het snel een breed beeld geeft van iemands persoonlijkheid in werksituaties. Dit geeft een onderbouwing aan de interviews en gesprekken met kandidaten. Het is dus belangrijk dat er niet alleen op de testscores wordt afgegaan bij selectie- en advies vraagstukken, maar dat er ook andere bronnen van informatie worden geraadpleegd, zoals een interview of andere tests, zoals tests over iemands werkwaarden en/of interesses.

Verder kan er qua interpretatie rekening worden gehouden met de mogelijke invloed van de achtergrondvariabelen op de testscores. Mensen kunnen namelijk verschillen in testscores vertonen op basis van hun geslacht, leeftijd, opleidingsniveau of etnische herkomst, losstaand van de intelligentie van deze persoon: iets wat we in kleine mate terugvinden bij de ACT Algemene Intelligentie (zie Hoofdstuk 6). We vinden bijvoorbeeld, net als in de literatuur en bij vele andere intelligentietests (zie bijvoorbeeld Van den Berg & Bleichrodt, 2000 en Van de Vijver, Bochhah, Kort & Seddik, 2001) dat kandidaten van allochtone afkomst wat lagere scores behalen dan kandidaten van autochtone afkomst. In Hoofdstuk 6 wordt het onderzoek naar deze relaties uitvoerig beschreven. De conclusie van deze onderzoeken was dat de verschillen in termen van effectgrootten relatief klein waren, wat betekent dat men rekening kan houden met verschillen op basis van achtergrondkenmerken, maar dat dit strikt genomen niet noodzakelijk is voor een juiste interpretatie (zie Hoofdstuk 4 voor een uitvoerige discussie hierover).

3.7. Software en ondersteuning

De ACT Algemene Intelligentie kan op iedere computer met internetverbinding met een werkende browser ingevuld worden. Er hoeft verder geen specifieke software geïnstalleerd te worden.

De portal ondersteunt alle veelgebruikte desktop internetbrowsers, zoals Microsoft Edge en recente versies van Chrome, Firefox en Safari onder Windows XP (en hoger), Apple OSX 10.4 of hoger en gangbare Linux versies. Het is mogelijk de test op de iPad te maken; wij raden dit echter af, omdat het selecteren van antwoorden (door middel van tikken met de vingers) minder eenvoudig is dan het klikken met de muis en dit voor sommige kandidaten problemen op kan leveren. Gezien de grote verschillen tussen tablets van andere merken wat betreft specificaties en beeldschermresoluties kunnen wij niet garanderen dat de ACT Algemene Intelligentie het op tablets van andere merken doet; dit raden wij dan ook af. Hetzelfde geldt voor smartphones. Gezien het feit dat tests voor selectieprocedures het best in rustige omgevingen gemaakt kunnen worden is het maken van de ACT Algemene Intelligentie op een computer of laptop aan te raden.

In de praktijk zullen niet al te strenge beveiligingsinstellingen of proxies geen probleem zijn. Daarnaast stelt het systeem technisch geen hoge eisen, zodat het in niet officieel ondersteunde browsers ook vrijwel altijd werkt.

Om de test in het online systeem te kunnen maken is verbinding met internet nodig. Mocht de internetverbinding tijdens het invullen van de test korte tijd wegvallen, dan ondervindt de kandidaat daar geen hinder van in de zin dat er resultaten verloren gaan. Mocht internet langere tijd uitvallen dan verschijnt de standaard ‘geen internet’ melding van de browser. Na opnieuw inloggen kan de kandidaat verder met de test, maar de test start dan wel bij de volgende opgave. Mocht dit gebeurd zijn dan raden wij de kandidaat aan contact op te nemen met zijn of haar coach of adviseur. Uit de praktijk is gebleken dat dit echter niet tot nauwelijks voor lijkt te komen.

Voor vragen over de systeemeisen en technische ondersteuning kunnen kandidaten contact opnemen met de helpdesk van Ixly. De helpdesk is iedere werkdag van 08.00 tot 17.30 bereikbaar via helpdesk@ixly.nl of 088-4959000.

Voor een overzicht van veel gestelde vragen met betrekking tot het gebruik van de testportal, zie Bijlage 3.2. In Bijlage 2.1. wordt een handleiding weergegeven voor de bediening van de software. De informatie over de bediening van de testportaal is ook te raadplegen via https://www.ixly.com/nl/test-toolkit-tutorial en https://www.ixly.com/nl/kennisbank/test-toolkit-faq/.

 

 

 

4. Normen

Bij de ACT Algemene Intelligentie gaat het om een normgerichte interpretatie. Dat wil zeggen dat de scores van een kandidaat worden vergeleken met een bepaalde normpopulatie. De normpopulaties bij de ACT Algemene Intelligentie zijn een representatie van de vier opleidingsniveaus VMBO, MBO, HBO en WO. Door middel van weging is er voor gezorgd dat de normgroepen qua leeftijd en geslacht overeenkomen met personen uit deze opleidingsniveaus in Nederland. Voor de berekening van de IQ-score is er tevens een normgroep die representatief is voor de beroepsbevolking wat betreft opleidingsniveau, leeftijd en geslacht. Voor deze verdelingen hebben we ons gebaseerd op gegevens van het Centraal Bureau voor de Statistiek (CBS) uit 2015. In dit hoofdstuk wordt nader beschreven hoe de normering is uitgevoerd en hoe de normgroepen zijn gevormd.

4.1. Normeringsonderzoek

 Doel normeringsonderzoek

 De ACT Algemene Intelligentie is primair ontwikkeld voor gebruik in selectieprocedures. Het is bekend dat kenmerken van situaties testscores kunnen beïnvloeden (zie ook Hoofdstuk 2, sectie 2.4.2. hierover). Bijvoorbeeld, scores verkregen onder ‘low-stakes’ situaties (zoals adviessituaties die bedoeld zijn om de testnemer inzicht te geven in zijn/haar gedrag zonder dat daar consequenties aan verbonden zijn) kunnen verschillen van scores verkregen in ‘high-stakes’ situaties. Selectieprocedures vallen onder ‘high-stakes’ situaties omdat er direct consequenties verbonden zijn aan de behaalde testscores, namelijk het krijgen van een baan. Gezien het gebruikersdoel van de ACT Algemene Intelligentie hebben wij er daarom voor gekozen de normgroepen te baseren op data verkregen in selectiesituaties uit de praktijk.

Er is voor gekozen om verschillende normgroepen te creëren voor verschillende opleidingsniveaus. Opleidingsniveau laat een zeer sterke relatie zien met intelligentie (zie bijvoorbeeld Strenze, 2007), wat ook aangetoond is bij de ACT Algemene Intelligentie (zie Hoofdstuk 6). Dit betekent dat het ‘oneerlijk’ zou zijn om bijvoorbeeld de scores op de ACT Algemene Intelligentie van iemand met een VMBO-opleiding te vergelijken met scores van iemand met een WO-opleiding. Bovendien is de ACT Algemene Intelligentie bedoelt voor de selectiepraktijk: organisaties zijn voor functies vrijwel altijd op zoek naar kandidaten met een bepaald opleidingsniveau. Functieprofielen bevatten dan ook standaard het opleidingsniveau dat benodigd is voor de functie. In de praktijk is het daarom nuttig om de scores van een kandidaat te kunnen vergelijken met de scores van personen met hetzelfde opleidingsniveau als de kandidaat, om zo de besten (degenen met relatief de hoogste scores) te kunnen selecteren.

Om normgroepen op basis van opleidingsniveau te creëren is hierom de database van Ixly geraadpleegd. In dit hoofdstuk wordt per normgroep uiteengezet hoe de dataverzameling en de normgroepen uiteindelijk tot stand gekomen zijn. Eerst volgt wat algemene achtergrondinformatie over dit proces.

Overige verschillen tussen groepen

 Voor de achtergrondvariabelen geslacht, leeftijd en etniciteit (allochtoon/autochtoon) hebben we een aantal significante verschillen gevonden in scores op de ACT Algemene Intelligentie. Het onderzoek hiernaar wordt uitvoerig beschreven in sectie 6.8. van Hoofdstuk 6. Uit dit onderzoek bleek dat de gevonden verschillen grotendeels overeenkwamen met de bevindingen van eerdere onderzoeken uit de literatuur. Bovendien waren de significante verschillen bij de achtergrondvariabelen, in termen van effectgrootte (Cohen, 1988), niet dusdanig dat ze grote praktische relevantie zullen hebben. Het kan interessant zijn de gevonden verschillen bij de interpretatie te betrekken aangezien het veelal reële verschillen betreft, maar dit is strikt genomen niet noodzakelijk (zie volgende sectie). Helaas hebben wij geen informatie over de etniciteit, regio, en werksector van de kandidaten die de ACT Algemene Intelligentie in selectieprocedures hebben gemaakt. Bij het kalibratieonderzoek is echter aangetoond dat er geen, of zeer kleine, verschillen te verwachten zijn wat betreft regio en werksector op de ACT Algemene Intelligentie.

Wel of geen aparte normen?

Los van de grootte van de te verwachte effecten, kan er discussie gevoerd worden over óf (al dan niet) reële verschillen door middel van verschillende normeringen ‘rechtgetrokken’ dienen te worden (Bochhah, Kort, Seddik, & Van de Vijver, 2001; Drenth, 1988; Tellegen, 2000; Van den Berg & Bleichrodt, 2000). De afwegingen die hierbij mogelijk een rol spelen kunnen het best verduidelijkt worden met een voorbeeld. Denk aan een coach van een gemengd korfbalteam, die selecteert op lengte, omdat de coach weet dat de kans groter is dat er gewonnen wordt met langere personen. Stel dat mannen gemiddeld 15 cm groter zijn dan vrouwen. Vervolgens komen er twee personen in aanmerking om geselecteerd te worden voor het team: een vrouw van 1.80m en een man van 1.85m. Omdat vrouwen gemiddeld kleiner zijn, zal de vrouw in vergelijking met andere vrouwen bovengemiddeld scoren wat betreft lengte (bijvoorbeeld een stenscore van 8). De man, daarentegen, zal in vergelijking met andere mannen gemiddeld zijn (bijvoorbeeld een stenscore 5). Zouden er dus aparte normgroepen qua lengte zijn voor mannen en vrouwen, dan zou de coach op basis van de behaalde gestandaardiseerde scores voor de vrouw kiezen. Echter, vergeleken met de totale populatie (mannen en vrouwen samen) zal de man een hogere gestandaardiseerde score (dat wil zeggen vergeleken met de normpopulatie) halen. Gezien zijn langere lengte is de kans groter dat hij beter zal presteren dan de vrouw. Anders gezegd, de coach wil de langste korfballer/korfbalster vergeleken met de populatie, niet de langste korfballer vergeleken met andere korfballers, of de langste korfbalster vergeleken met andere korfbalsters. Als voor personen uit verschillende groepen andere maatstaven gelden dan kunnen deze personen niet meer met elkaar vergeleken worden (Tellegen, 2000).

Dit voorbeeld is ook van toepassing op de ACT Algemene Intelligentie; uit eerder onderzoek is bijvoorbeeld gebleken dat fluid intelligence vanaf de adolescentie langzaam afneemt met leeftijd (zie bijvoorbeeld Kaufman & Horn, 1996). Het zal echter niet wenselijk zijn deze reële verschillen ‘weg te normeren’: ook hier geldt weer dat een organisatie hoogstwaarschijnlijk de persoon met het hoogste intelligentieniveau aan zal willen nemen (vergeleken met andere personen uit zijn/haar opleidingsniveau), niet de persoon met het hoogste intelligentieniveau in vergelijking met personen van zijn/haar leeftijd. Hetzelfde geldt voor geslacht, hoewel de gevonden verschillen bij de ACT Algemene Intelligentie van zo’n geringe grootte zijn dat deze überhaupt weinig praktische relevantie zullen hebben (zie Hoofdstuk 6).

Het kan natuurlijk zo zijn dat de coach een gelijke verdeling wil wat betreft mannen en vrouwen in zijn/haar team, maar dan spelen er hele andere overwegingen (namelijk diversiteit) een rol dan puur een winst- of prestatiemaximalisatie. In de selectiepraktijk is het uiteindelijk een beleidsbeslissing welk evenwicht tussen ‘gelijke kansen’ en ‘doelmatigheid’ in de gegeven omstandigheden en binnen de economische en politieke randvoorwaarden de voorkeur verdient (Drenth, 1988).

Dit voorbeeld maakt duidelijk dat altijd het doel voor ogen gehouden dient te worden waarvoor een test gebruikt wordt. Iemand die bijvoorbeeld van het buitenland naar Nederland verhuist om in Nederland te komen werken zal afgezet dienen te worden tegen de Nederlandse beroepsbevolking (in tegenstelling tot de beroepsbevolking van het herkomstland) omdat hij/zij uiteindelijk zal werken en moet presteren in de Nederlandse arbeidsmarkt. Vanzelfsprekend dient er dan wel voor gezorgd te worden dat hij/zij de Nederlandse taal voldoende machtig is (als de test in het Nederlands afgenomen wordt) of, als de test in de taal van het herkomstland afgenomen wordt, dat meetinvariantie van de vertaalde test voldoende is aangetoond. Dit om vertekeningen in testscores te voorkomen.

Daarom onderschrijven wij de aanbeveling (Ter Laak & Van Luijk, zoals geciteerd in Bochhah, Kort, Seddik, & Van de Vijver, 2001) dat personen uit verschillende groepen goed met de ‘algemene’ normpopulatie vergeleken kunnen worden, maar dat inachtneming van de achtergrond, kenmerken en bijzonderheden van de kandidaat belangrijk kan zijn – zij het in een vroeg stadium van het selectieproces, of bij de interpretatie en terugkoppeling van de behaalde testscores en/of bijvoorbeeld tijdens het interview.  Zo kan er bijvoorbeeld bij de interpretatie van testscores van allochtone kandidaten rekening worden gehouden met de individuele achtergrond van de kandidaat, zoals verblijfsduur, etnische achtergrond en het taalvaardigheidsniveau (Van den Berg & Bleichrodt, 2000). De gegevens zoals beschreven in Hoofdstuk 6, sectie 6.8.4., kunnen hierbij helpen. Bijvoorbeeld: als een kandidaat met een migratieachtergrond een relatief lage, afwijkende score op Verbale Analogieën laat zien, terwijl hij/zij relatief hoger op Figurenreeksen en Cijferreeksen scoort, dan kan met de kandidaat besproken worden wat hier mogelijke oorzaken zijn – wellicht wordt er thuis geen Nederlands gesproken. Ook kan men bijvoorbeeld allochtonen vergelijken met de algemene normtabel en binnen de groep allochtonen vervolgens de besten, of degenen die boven een bepaald minimum scoren, selecteren (Te Nijenhuis & Evers, 2000).

Om bovenstaande redenen hanteren we dus geen aparte normgroepen op basis van geslacht, regio, leeftijd of etniciteit.

Algemene opmerkingen over normeringsonderzoek

De data zijn verzameld bij een groot aantal organisaties, verspreid door het hele land, en uit allerlei sectoren. De data zijn dan ook verzameld voor selectie van personeel in (onder andere) de (online) retail sector, bij gezondheidsorganisaties, in finance, inkoop, business intelligence, logistiek, luchtvaart, transport, techniek/industrie, de zorg, het onderwijs, de mediasector als ook in de publieke sector. Bovendien bestaat een deel van de klanten van Ixly uit selectie- en assessmentbureaus: zij zetten de ACT Algemene Intelligentie in voor verschillende opdrachtgevers uit verschillende sectoren. Qua verscheidenheid aan typen banen en sectoren kunnen wij dus verwachten dat de verzamelde resultaten op de ACT Algemene Intelligentie divers genoeg zijn.

De analyses uit de overige hoofdstukken uit deze handleiding zijn gedaan tussen juli en december 2016, en dus gebaseerd op data tot en met juli 2016. Omdat de VMBO-, HBO- en WO-normgroepen op basis van deze data van een relatief kleine omvang waren en omdat de MBO-groep weinig divers was, is aan de normgroepen nieuwe data verkregen in selectiesituaties toegevoegd, verzameld tussen juli 2016 en december 2016.

De testscores zouden vertekend kunnen zijn als deze voornamelijk bij één klant verzameld zouden zijn, omdat deze bijvoorbeeld alleen tests inzetten voor sollicitaties binnen een bepaalde sector. Daarom hebben we getracht zo divers mogelijke databronnen te gebruiken voor de normgroepen en de normgegevens dus verzameld bij zoveel mogelijk verschillende klanten en bedrijven uit verschillende sectoren. Een streven hierbij was dat maximaal 20% van de kandidaten binnen een bepaalde normgroep bij één databron afkomstig mocht zijn. Dit is grotendeels gelukt, alleen voor de VMBO-groep niet: daarom moet deze normgroep als een voorlopige normgroep beschouwd worden. Hieronder wordt dit nader toegelicht. Ook wordt de representativiteit van de normgroepen besproken. In alle gevallen waren, volgens de richtlijnen van de Cotan (2009), de maximale wegingsfactoren in het kader van representativiteit op de variabelen geslacht en leeftijd niet groter dan 2, tenzij anders vermeld.

4.2. Beschrijving normgroepen

In Tabel 4.1. en Tabel 4.2. zijn de kenmerken van de normgroepen voor en na weging weergegeven, en de verdeling van de achtergrondkenmerken in de normpopulaties zoals verkregen via het CBS. Hieronder volgt per normgroep een beschrijving van de relevante kenmerken. Bij de kwalificering van de grootte van de correlaties tussen de scores op de ACT Algemene Intelligentie en geslacht/leeftijd[1] hebben we de richtlijnen van Cohen (1988, 1992) gehanteerd: <.10: triviaal, .10 – .30: klein tot gemiddeld, .30 – .50: gemiddeld tot groot, >.50: groot tot zeer groot.

Tabel 4.1. Verdelingen geslacht en leeftijd, VMBO en MBO.
	VMBO				MBO
	Onderzoeks-   groep (N = 321)	Gewogen normgroep   (N = 300)	CBS   2015 %		Onderzoeks-   groep (N = 659)	Gewogen normgroep   (N = 659)	CBS   2015 %
Geslacht:
Man	252 (78.5)	183 (61.0)	55.7		349 (53.0)	358 (54.3)	53.1
Vrouw	69 (21.5)	117 (39.0)	44.3		310 (47.0)	301 (45.7)	46.9
Leeftijd:
15-24 jaar	62 (19.3)	90 (30.0)	30.5		60 (9.1)	114 (17.4)	17.4
25-44 jaar	179 (55.8)	96 (32.0)	26.0		310 (47.0)	268 (40.7)	40.7
45-65 jaar	80 (24.9)	114 (38.0)	43.5		289 (43.9)	277 (42.0)	42.0

VMBO

In totaal hadden we testscores van 321 personen met VMBO-niveau, verkregen tussen juli 2015 en december 2016. Bij deze groep was 74% van de data verkregen bij één specifieke klant uit de transportsector. De overige data waren verkregen bij 21 andere databronnen. Dit zorgde voor een scheve verdeling wat betreft mannen en vrouwen in de onderzoeksgroep: in totaal was 78.5% man (Tabel 4.1.). Ook de verdeling wat betreft leeftijd in de drie categorieën 15 t/m 25, 26 t/m 45 en 46 t/m 65 week sterk af van de verdeling in de normpopulatie. Door middel van weging[2] is geprobeerd voor deze vertekening te corrigeren. Een tweede doel hierbij was de normgroep zo groot mogelijk te houden. Uiteindelijk heeft deze weging geleid tot de, in Tabel 4.1., weergegeven verdeling wat betreft leeftijd en geslacht. De verdeling wat betreft geslacht (χ²(1) = 3.39, p = .07) verschilde na weging niet significant van de respectievelijke verdeling in de normpopulatie. De leeftijdsverdeling verschilde nauwelijks van de leeftijdsverdeling in de normpopulatie (χ²(2) = 6.28, p = .04, V = .10). Echter, er kon helaas net niet voldaan worden aan de gestelde eis (Cotan, 2009) dat de maximale weging <2 mag zijn (de maximale weging was 2.32). Bovendien is door weging de gewogen N 300 geworden (ten opzichte van een ongewogen N van 321).

De gemiddelde leeftijd in de gewogen VMBO-normgroep was 37.5 jaar (SD = 13.8, Min.-Max = 17-63). De vrouwen (M = 46.9, SD = 14.0) waren significant en aanzienlijk ouder dan mannen (M = 31.5, SD = 10.4) in deze steekproef (F(1,297) = 124.8, p = .00, Cohen’s d = -1.25). Voor Cijferreeksen, Figurenreeksen en g-score scoorden vrouwen significant lager dan mannen, hoewel de effectgrootten duidden op verschillen van klein tot gemiddelde grootte (respectievelijk r = -.25, -.30, -.24). Hetzelfde gold voor de gevonden negatieve effecten van leeftijd op de g-score en scores op Cijferreeksen en Figurenreeksen (respectievelijk r = -.15, -.15, -.31). Een lineaire regressie toonde verder aan dat het effect van leeftijd verdween voor Cijferreeksen (B = -.001, p = .84) en de g-score (B = -.001, p = .65) wanneer gecontroleerd werd voor sekse.

Gezien het feit dat een groot deel van de data afkomstig was van één bron en het feit dat de maximale weging >2 was, moet deze normgroep als een voorlopige normgroep beschouwd worden. Echter, gezien de scoreverdeling (Tabel 4.3.) lijkt deze groep een redelijke weergave te zijn van personen met een VMBO opleiding in de Nederlandse beroepsbevolking.

MBO

In totaal hadden we van 1213 personen (verzameld tussen juli 2015 en december 2016) de testscores op de ACT Algemene Intelligentie. Ook bij deze groep was een groot deel van de data verkregen bij dezelfde bron als waar de VMBO-data waren verkregen (685 personen; 56.5%). Om de representativiteit van de normgroep te waarborgen is daarom uit deze 685 personen een willekeurige steekproef getrokken die in de uiteindelijke normgroep terecht zijn gekomen. Het aantal personen dat getrokken werd uit deze specifieke groep werd bepaald door de eis dat in de uiteindelijke normgroep niet meer dan 20% bij één databron verzameld mocht zijn. Uiteindelijk betekende dit dat er 131 personen willekeurig uit deze groep getrokken zijn. In totaal zijn de data bij 66 databronnen verzameld. Er waren drie bronnen met een redelijk groot aandeel (twee van 20% en één met 15%), maar over het algemeen leverde iedere databron slechts een klein aantal kandidaten. Het gemiddelde percentage verkregen bij een databron was 1.5% (mediaan was 0.3%). Hiermee is gewaarborgd dat er niet één databron is geweest die oververtegenwoordigd is in deze normgroep en dat er een grote verscheidenheid aan kandidaten wat betreft sector aanwezig is.

De uiteindelijke normgroep bestond uit 659 personen. De verdeling wat betreft geslacht was nagenoeg identiek aan de verdeling in de normpopulatie (χ²(1) = .00, p = .95), terwijl er naar verhouding iets te weinig jongeren in de steekproef zaten en te veel personen tussen de 25 en 45 jaar (χ²(2) = 33.04, p = .00). Door middel van weging is ervoor gezorgd dat verdeling qua leeftijd representatief was voor de normpopulatie. Ook na weging was de steekproef nog representatief wat betreft geslacht (χ²(1) = .41, p = .53).

De gemiddelde leeftijd in de gewogen MBO-normgroep was 40.1 jaar (SD = 12.3, Min.-Max = 19-64). De vrouwen (M = 42.8, SD = 11. 4) waren significant ouder dan mannen (M = 37.9, SD = 10.4) in deze steekproef (F(1,657) = 27.7, p = .00), hoewel dit verschil niet al te groot was (d = -.41). De negatieve correlaties met geslacht (vrouwen scoorden lager dan mannen op alle onderdelen van de ACT Algemene Intelligentie in deze normgroep; respectievelijk r = -.29, -.15, -13 en -.25 voor Cijferreeksen, Figurenreeksen, Verbale Analogieën en de g-score) en leeftijd (r = -.15, -.24 en -.15 voor respectievelijk Cijferreeksen, Figurenreeksen en de g-score) zijn van een kleine tot gemiddelde omvang. Er werd geen effect van leeftijd op Verbale Analogieën gevonden.

Tabel 4.2. Verdelingen geslacht en leeftijd, HBO en WO.
	HBO				WO
	Onderzoeks-   groep (N = 570)	Gewogen normgroep   (N = 570)	CBS   2015 %		Onderzoeks-   groep (N = 490)	Gewogen normgroep   (N = 490)	CBS   2015 %
Geslacht:
Man	314 (55.1)	287 (50.3)	50.3		258 (52.7)	272 (55.5)	52.8
Vrouw	256 (44.9)	283 (47.6)	47.6		232 (47.3)	218 (44.5)	47.2
Leeftijd:
15-24 jaar	40 (7.0)	41 (7.2)	7.0		75 (15.3)	11 (2.3)	2.3
25-44 jaar	315 (55.3)	315 (55.3)	53.5		317 (64.7)	278 (56.7)	56.7
45-65 jaar	215 (37.7)	214 (37.5)	39.5		98 (20.0)	201 (41.0)	41.0

 

 HBO

In totaal zijn er van 570 kandidaten gegevens verzameld bij 67 databronnen (tussen juli 2015 en december 2016), waarbij maximaal ongeveer 20% door één databron geleverd werd. Het gemiddelde percentage kandidaten per bron was echter 1.5% (mediaan 0.4%).

Wat betreft representativiteit qua geslacht waren mannen licht oververtegenwoordigd in de steekproef (χ²(1) = 5.30, p = .02). De steekproef was representatief wat betreft de drie leeftijdscategorieën, in vergelijking met de normpopulatie (χ²(2) = .76, p = .68). Door middel van weging is er voor gezorgd dat de normgroep volledig representatief werd qua sekse. Ook de gewogen normgroep was representatief wat betreft leeftijd (χ²(2) = .88, p = .64).

De gemiddelde leeftijd in de gewogen HBO-normgroep was 39.8 jaar (SD = 11.2, Min.-Max = 18-67). De vrouwen (M = 40.9, SD = 10.6) waren iets jonger dan mannen (M = 38.8, SD = 11. 9) in deze normgroep (F(1,568) = 4.6, p = .03), hoewel dit verschil klein was (d = .18). Er werd geen effect van leeftijd en geslacht op scores op de subtest Verbale Analogieën gevonden. De overige negatieve correlaties met leeftijd (r = -.19, -.31, -.22 voor Cijferreeksen, Figurenreeksen en de g-score) en geslacht (vrouwen scoorden lager dan mannen; r = -.16, -.14 en -.12 voor Cijferreeksen, Figurenreeksen en de g-score) zijn van een kleine tot gemiddelde omvang.

 WO

In totaal hadden we van 490 kandidaten met een WO-opleiding testgegevens, verzameld tussen juli 2015 en december 2016. Deze gegevens waren verzameld bij 56 databronnen. Bij de WO-groep kon niet geheel voldaan worden aan de eis dat één bron een niet te groot aandeel mocht hebben in de normgroep: één databron was verantwoordelijk voor ongeveer 27% van de kandidaten in deze normgroep. Het gemiddelde percentage kandidaten per bron was echter 1.8% (mediaan 0.3%).

De ongewogen normgroep was representatief voor de normpopulatie wat betreft geslacht (χ²(1) = .00, p = .95). Qua leeftijd waren jongeren en ouderen ondervertegenwoordigd in de steekproef (χ²(2) = 418.99, p = .00; zie Tabel 4.2.). Daarom is er door middel van weging voor gezorgd dat de uiteindelijke normgroep volledig representatief was wat betreft leeftijd in vergelijking met de normpopulatie. Ook na weging was de steekproef nog representatief wat betreft geslacht (χ²(1) = 1.46, p = .23).

De gemiddelde leeftijd in de gewogen WO-normgroep was 39.2 jaar (SD = 11.3, Min.-Max = 22-62). Mannen (M = 38.6, SD = 11.7) verschilden niet significant van vrouwen (M = 39.9, SD = 10. 9) qua leeftijd (F(1,488) =.29, p = .59). Er werden geen verschillen gevonden tussen mannen en vrouwen op de subtest Verbale Analogieën. De sekseverschillen op de overige onderdelen waren klein van omvang (r = -.12, -.15, -.14 voor Cijferreeksen, Figurenreeksen en de g-score). Het negatieve effect van leeftijd op de behaalde scores was van kleine tot gemiddelde omvang voor Cijferreeksen (r = -.36) en Verbale Analogieën (r = -.23), terwijl voor Figurenreeksen (r = -.46) en de g-score (r = -.45) het effect als gemiddeld tot groot gekwalificeerd kan worden.

De hoge correlaties tussen leeftijd en de g-score en de scores op de subtest Figurenreeksen zijn aan de hoge kant. Uit de literatuur zijn deze effecten niet eenvoudig te verklaren: onderzoeken kijken voornamelijk naar de relatie tussen leeftijd en intelligentie in de gehele populatie, niet voor verschillende opleidingsniveaus afzonderlijk.

Deze effecten lijken dan ook voort te komen uit de specifieke samenstelling van de normgroep. Inspectie van deze normgroep liet zien dat de personen van wie de scores verkregen waren bij de grootste databron aanzienlijk jonger waren dan personen waarvan de scores verkregen waren bij andere organisaties (M = 25.6 jaar, SD = 3.4 in vergelijking met M = 37.1 jaar, SD = 10.4, ||d|| = 1.49). De lagere standaarddeviatie geeft ook aan dat deze groep zeer homogeen was wat betreft leeftijd. Het bleek ook dat deze groep aanzienlijk hoger scoorde op de ACT Algemene Intelligentie dan de rest van de normgroep (g-score: M = 1.17, SD =.40 in vergelijking met M = .84, SD = .49, ||d|| = .73). Deze combinatie van effecten lijkt hiermee deels verantwoordelijk voor de hoge correlaties tussen de testscores en leeftijd.

Zonder deze specifieke groep waren de correlaties tussen Cijferreeksen, Figurenreeksen, Verbale Analogieën en de g-score en leeftijd respectievelijk -.30, -.41, -.18 en -.38. Hoewel nog steeds aan de hoge kant, gaan deze correlaties wel in de richting van acceptabelere waarden.

De oplossing hiervoor lijkt dus vooral te liggen in het verzamelen van meer testscores bij verschillende organisaties om een meer representatief beeld van de WO-groep te krijgen. In de toekomst zullen we zo spoedig mogelijk de normgroep WO aanvullen met nieuwe testgegevens om de huidige tekortkomingen tegen te gaan.

Beschrijving van schaalkenmerken in de normgroepen

In Tabel 4.3. tot en met Tabel 4.6. zijn de kenmerken van de ruwe  scores (θ) op de schalen van de ACT Algemene Intelligentie weergegeven voor de gewogen normgroepen. Zo krijgt de gebruiker een beeld van de verdeling van de ruwe scores in de normpopulaties.

Tabel 4.3. Kenmerken van de ruwe scores (θ) op de ACT Algemene Intelligentie, normgroep VMBO (N = 300).
	Min.	Max.	Gem.	SD	Scheefheid			Kurtosis
					Waarde	SE	Waarde		SE
Cijferreeksen	-2.33	2.53	-.33	.64	.24	.14	.58		.28
Figurenreeksen	-1.90	1.91	-.23	.64	.12	.14	.14		.28
Verbale Analogieën	-2.61	1.99	-.18	.75	-.35	.14	.47		.28
g-score	-1.97	1.29	-.24	.53	-.12	.14	.12		.28

 

Tabel 4.4. Kenmerken van de ruwe scores (θ) op de ACT Algemene Intelligentie, normgroep MBO (N = 659).
	Min.	Max.	Gem.	SD	Scheefheid			Kurtosis
					Waarde	SE	Waarde		SE
Cijferreeksen	-2.42	2.23	-.12	.70	.24	.10	.52*		.19
Figurenreeksen	-2.19	2.42	-.06	.78	.36*	.10	.19		.19
Verbale Analogieën	-2.50	2.38	.05	.77	-.46*	.10	.18		.19
g-score	-2.11	1.74	-.04	.61	-.21	.10	.08		.19

 

Tabel 4.5. Kenmerken van de ruwe scores (θ) op de ACT Algemene Intelligentie, normgroep HBO (N = 570).
	Min.	Max.	Gem.	SD	Scheefheid			Kurtosis
					Waarde	SE	Waarde		SE
Cijferreeksen	-1.77	2.58	.42	.78	.31*	.10	.05		.20
Figurenreeksen	-1.96	2.44	.42	.78	.21	.10	-.44		.20
Verbale Analogieën	-1.75	2.39	.64	.66	-.53*	.10	1.42*		.20
g-score	-1.60	2.01	.50	.56	-.32*	.10	.56*		.20

 

Tabel 4.6. Kenmerken van de ruwe scores (θ) op de ACT Algemene Intelligentie, normgroep WO (N = 490)
	Min.	Max.	Gem.	SD	Scheefheid			Kurtosis
					Waarde	SE	Waarde		SE
Cijferreeksen	-1.12	2.70	.77	.77	.23	.11	-.25		.22
Figurenreeksen	-0.97	2.46	.80	.78	.04	.11	-.75*		.22
Verbale Analogieën	-0.77	2.55	.94	.54	.16	.11	.48		.22
g-score	-0.48	2.29	.83	.50	-.16	.11	-.18		.22

 

Met een asterisk (*) is aangegeven wanneer de Z-score (verkregen door de waardes door hun standaardfout te delen) van de scheefheid en kurtosis (platheid) de grens ± 2.58 overstijgt. Deze drempelwaarde wordt vaak gehanteerd als indicatie dat een verdeling van de theoretische normale verdeling afwijkt. Voor de VMBO- en de WO-normgroepen geldt dat alle waarden van de scheefheid en kurtosis tussen de – 2.58 en + 2.58 liggen. Bij de MBO- en HBO-groep is dit niet het geval. Bij de MBO-normgroep laten de testscores op Figurenreeksen en Verbale Analogieën naar verhouding wat scheve verdelingen zien, terwijl de verdeling van Cijferreeksen een wat grotere piek dan verwacht laat zien. Bij de HBO-normgroep laten de testscores op Cijferreeksen, Verbale Analogieën en g-scores naar verhouding scheve verdelingen zien, terwijl de verdeling van de g-score en met name Verbale Analogieën een grotere piek dan verwacht laat zien. Echter, de vuistregel van ||Z||>2.58 wordt door sommigen als erg streng gekwalificeerd, en zij hanteren daarom meer liberalere regels waarbij absolute waarden van scheefheid > 3 en kurtosis > 8 (of zelf >10) gelden als een indicatie voor een afwijking van de normale verdeling (Kline, 2005). Gebaseerd op deze regels kunnen we over het algemeen dus concluderen dat de testscores van de ACT Algemene Intelligentie redelijk normaal verdeeld zijn in de vier normgroepen.

Normgroep beroepsbevolking ten behoeve van IQ-score

 Aangezien de ACT Algemene Intelligentie ook IQ-scores rapporteert, waarbij de scores op de ACT Algemene Intelligentie dus niet vergeleken worden met een bepaald opleidingsniveau maar met de gehele populatie, is er ook een normgroep ontwikkeld die representatief is voor de gehele beroepsbevolking van Nederland. Deze normgroep is gebaseerd op de vier (ongewogen) normgroepen, plus aanvullende data verkregen bij personen die de ACT Algemene Intelligentie in selectiesituaties hebben gemaakt. Zo zijn de scores op de ACT Algemene Intelligentie van 2761 personen verzameld bij 111 verschillende organisaties. Het maximaal aandeel van één organisatie was 39.4%[3]; het gemiddelde aandeel was 0.9% (mediaan = 0.1%). De verdeling wat betreft opleidingsniveaus in de totale normgroep is weergegeven in Tabel 4.7.

Tabel 4.7. Verdeling opleidingsniveaus in normgroep beroepsbevolking, ongewogen.
	Freq.	%
Lagere school/basisonderwijs	38	1.4
VMBO	321	11.6
MBO	1213	43.9
HAVO	79	2.9
VWO	50	1.8
HBO	570	20.6
WO	490	17.7
Totaal	2642	100

 

In Tabel 4.8. zijn de kenmerken van de beroepsbevolking normgroep voor en na weging weergegeven, en de verdeling van de achtergrondkenmerken in de normpopulatie (totale beroepsbevolking) zoals verkregen via het CBS. In de ongewogen normgroep waren mannen oververtegenwoordigd. Dit gold ook voor personen van middelbare leeftijd en personen met een hoger opleidingsniveau. Mensen van hogere leeftijd en lager opleidingsniveau waren ondervertegenwoordigd. Aangezien opleidingsniveau de sterkste relatie laat zien met de scores op de ACT Algemene Intelligentie, is er bij de weging voor gekozen de normgroep voor dit achtergrondkenmerk volledig representatief voor de normpopulatie te laten zijn. Bij de weging speelden daarom verschillende doelen een rol: de wegingsfactor mocht niet groter dan 2 zijn, de normgroep moest representatief zijn wat betreft opleidingsniveau en de gewogen normgroep moest zo groot mogelijk blijven. Deze drie afwegingen samen hebben uiteindelijk geresulteerd in de verdeling wat betreft sekse, leeftijd en geslacht zoals weergegeven in de derde kolom van Tabel 4.8. De gewogen normgroep verschilde enigszins van de normpopulatie wat betreft geslacht (χ²(1) = 25.04, p = .00) en leeftijd (χ²(2) = 80.09, p = .00), maar deze verschillen waren relatief klein (Cramer’s V respectievelijk .07 en .12).

Tabel 4.8. Verdelingen geslacht, leeftijd en opleiding, beroepsbevolking.
	Beroepsbevolking
	Onderzoeks-   groep (N = 2761)	Gewogen normgroep   (N = 2761)	CBS   2015 %
Geslacht:
Man	1793 (64.9)	1601 (58.0)	53.2
Vrouw	968 (35.1)	1160 (42.0)	46.8
Leeftijd:
15-24 jaar	359 (13.0)	500 (18.1)	16.1
25-44 jaar	1497 (54.2)	1408 (51.0)	42.1
45-65 jaar	905 (32.8)	853 (30.9)	41.8
Opleiding:
Laag	359 (13.0)	623 (22.6)	22.6
Midden	1342 (48.6)	1180 (42.7)	42.7
Hoog	1060 (38.4)	959 (34.7)	34.7

 

 De gemiddelde leeftijd in de gewogen normgroep was 37.2 jaar (SD = 11.9, Min.-Max = 17-67). Vrouwen (M = 38.3, SD = 13. 3) waren significant ouder dan mannen (M = 36.3, SD = 11.0) in deze steekproef (F(1,2759) = 18.9, p = .00), hoewel dit verschil klein was (d = -.16).

De correlaties met geslacht zijn alleen significant voor Verbale Analogieën en de g-score, maar klein wat betreft effectgrootte (respectievelijk r = .10 en r = .05; vrouwen scoorden iets hoger dan mannen). De negatieve correlaties met leeftijd zijn van iets grotere omvang, maar kunnen nog steeds als klein tot gemiddeld aangeduid worden (respectievelijk r = -.18, -.27, -.08 en -.18 voor Cijferreeksen, Figurenreeksen, Verbale Analogieën en de g-score).

In Tabel 4.9. zijn de kenmerken van de ruwe  scores (θ) op de schalen van de ACT Algemene Intelligentie weergegeven voor de totale gewogen normgroep.

Tabel 4.9. Kenmerken van de ruwe scores (θ) op de ACT Algemene Intelligentie, normgroep beroepsbevolking (N = 2761).
	Min.	Max.	Gem.	SD	Scheefheid			Kurtosis
					Waarde	SE	Waarde		SE
Cijferreeksen	-2.42	2.70	.10	.84	.31*	.05	.11		.09
Figurenreeksen	-2.22	2.46	.18	.85	.26*	.05	-.26*		.09
Verbale Analogieën	-2.76	2.55	.26	.84	-.35*	.05	.16		.09
g-score	-2.11	2.29	.18	.71	-.08	.05	-.24		.09

 

Hoewel enkele Z-waarden van scheefheid en kurtosis (verkregen door deze te delen door hun standaardfout) groter waren dan 2.58, werd ruimschoots aan de alternatieve criteria gesteld door Kline (2005) voldaan. We kunnen dus concluderen dat de testscores van de ACT Algemene Intelligentie redelijk normaal verdeeld zijn in de totale normgroep.

Bij de ACT Algemene Intelligentie worden de ruwe scores omgezet naar gestandaardiseerde scores, zodat de ruwe score vergeleken kan worden met de normgroep. Deze gestandaardiseerde scores worden in de volgende sectie besproken (zie ook Hoofdstuk 3).

4.3. Gebruikte scores en normtabellen

Bij de ACT Algemene Intelligentie worden de stenscores, T-scores, percentielscores en IQ-scores gerapporteerd. Per schaal wordt de ruwe schaalscores omgezet in een Z-score en vervolgens in de vier genoemde gestandaardiseerde scores. Standaardscores geven een beeld van de manier waarop een bepaalde score zich verhoudt tot de normpopulaties, in ons geval de vier genoemde opleidingsniveaus en de Nederlandse beroepsbevolking. Hoe deze scores precies tot stand komen en hoe men deze scores dient te interpreteren wordt besproken in het Hoofdstuk 3.

In Bijlage 4.1. en Bijlage 4.2. zijn de normtabellen van de  schalen opgenomen. In deze tabellen wordt voor iedere ruwe score de bijbehorende stenscore, T-score, percentielscore en IQ-score weergegeven. Ook wordt voor de stenscore het betrouwbaarheidsinterval (horend bij een betrouwbaarheidsniveau van 80%, 90% en 95%) gegeven. Een betrouwbaarheidsniveau van 80% wil zeggen dat bij een groot aantal herhalingen van de voorspelling of schatting van een score X, 80% van de berekende intervallen de onbekende waarde X bevat (Drenth & Sijtsma, 2006).

We hebben ervoor gekozen dit interval voor de stenscore te geven omdat ervaring geleerd heeft dat de meeste gebruikers de stenscores gebruiken bij de terugkoppeling van de scores, en omdat dit interval ook weergegeven is in het rapport (zie Bijlage 3.1. voor een voorbeeldrapport).

Stenscores zijn een vorm van standaardscores met een gemiddelde van 5.5 en een standaarddeviatie van 2. Het 80%-betrouwbaarheidsinterval wordt daarom als volgt berekend:

Ondergrens betrouwbaarheidsinterval:            5.5 + 2 * (Z – 1.28 * SEM)

Bovengrens betrouwbaarheidsinterval:            5.5 + 2 * (Z + 1.28 * SEM)

Hierin is Z de score die verkregen wordt door van de ruwe θ-score het gemiddelde van de normgroep af te trekken en te delen door de standaarddeviatie van deze normgroep:

De waarde 1.28 correspondeert met het 80%-betrouwbaarheidsinterval, de bijbehorende waarden voor het 90%- en 95%-betrouwbaarheidsinterval zijn respectievelijk 1.68 en 1.96. Hoe hoger het betrouwbaarheidsniveau, hoe breder het betrouwbaarheidsinterval.

Bij tests die gebaseerd zijn op de klassieke testtheorie (in tegenstelling tot itemresponstheorie waar de ACT Algemene Intelligentie op gebaseerd is) is de betrouwbaarheid één maat, die iets zegt over de nauwkeurigheid van de gehele schaal. In de itemresponstheorie is de betrouwbaarheid van de meting afhankelijk van de locatie op de θ-schaal (zie Hoofdstuk 5). Daarom zijn in Bijlage 4.1. en 4.2. de normtabellen weergegeven op basis van verschillende SEM-maten. De eerste variant in Bijlage 4.1. is de SEM berekend op basis van de gehele itembank: dat wil zeggen dat per subtest voor de waarden -2.5 tot en met 2.5 (in stapjes van 0.1) de informatie geleverd door alle subtestitems is opgeteld, resulterend in de totale informatie (TI) per θ-waarde. Vervolgens is met de formule 1/√TI de SEM berekend voor iedere waarde van θ. De SEM van de g-score is berekend door de som te nemen van de informatiewaarden geleverd door alle items (dus van alle drie de subtest samen) bij iedere θ-waarde, en vervolgens weer de SEM te berekenen met bovenstaande formule.

Deze weergave is echter enigszins misleidend, omdat dit om de SEM zou gaan wanneer een kandidaat alle mogelijk items uit de itembank voorgeschoteld zou krijgen. Echter, in de ACT Algemene Intelligentie beantwoordt iedere kandidaat slechts een kleine portie hiervan (minimaal 10, maximaal 17 per subtest). Om een reëler beeld te geven van de SEM en de daarbij behorende betrouwbaarheidsintervallen die men mag verwachten bij de ACT Algemene Intelligentie is er een simulatiestudie uitgevoerd. In deze studie werden eerst voor iedere waarde tussen de -2.5 en 2.5 in stapjes van 0.1 steeds 500 ‘personen’ – dus θ’s – gegenereerd. Er waren dus 500 ‘ware θ’s’ met waarde -2.5, 500 ‘ware θ’s’ met waarde -2.4, 500 ‘ware θ’s’ met waarde -2.3 et cetera. Dit resulteerde in een totale N van 25500. Vervolgens werd voor deze 25500 personen de ACT Algemene Intelligentie gesimuleerd. Hierna werd voor iedere 500 kandidaten met dezelfde ware θ de gemiddelde SEM berekend, resulterend in 51 gemiddelde SEM-waarden (namelijk voor iedere waarde tussen de -2.5 en 2.5). Dit zijn SEM-waarden die we dus mogen verwachten voor waarden over de gehele θ-schaal. Deze gemiddelde SEM-waarden zijn vervolgens weergegeven in de normtabellen in Bijlage 4.2. en gebruikt om de betrouwbaarheidsintervallen te berekenen.

[1] Omdat in sommige groepen slechts een klein aantal personen zaten of de verdelingen over categorieën erg scheef was hebben we ervoor gekozen met correlaties te werken in plaats van groepsverschillen.

[2] Voor alle wegingen is gebruik gemaakt van de SPSS-macro verkregen via http://mr-serv.com/spss-multi-level-weighting. In deze macro wordt een algoritme gehanteerd wat er voor zorgt dat er multivariaat gewogen wordt voor meerdere onafhankelijke criteria (namelijk de proportie mannen/vrouwen en de proportie laag/midden/hoge leeftijd.

[3] We hebben besloten in deze totale normgroep alle data van de eerder genoemde organisatie uit de transportsector te gebruiken. Vergeleken met andere MBO’ers (N = 528) verschilden de scores van personen uit deze groep (N = 685) niet op de subtest Cijferreeksen en de g-score. Het verschil in scores op Figurenreeksen en Verbale Analogieën was klein (respectievelijk d = -.14 en d = .16).

 

 

5. Betrouwbaarheid 

5.1. Inleiding

De betrouwbaarheid van een vragenlijst geeft een indicatie van de nauwkeurigheid van het instrument. Het begrip heeft betrekking op de reproduceerbaarheid van de gemeten uitkomsten; in hoeverre komen de resultaten van een meting met het instrument bij een tweede keer (en derde keer, enzovoorts) overeen, of in hoeverre komen de uitkomsten bij een vergelijkbare set items overeen? In dit hoofdstuk worden de onderzoeken met betrekking tot de betrouwbaarheid van de ACT Algemene Intelligentie beschreven.

Hoofdstuk 1 moet al duidelijk gemaakt hebben dat bij IRT-modellen het klassieke idee van betrouwbaarheid niet op gaat: de mate van de nauwkeurigheid van de meting is namelijk afhankelijk van de locatie waar op de θ-schaal gemeten wordt. Toch is het soms wenselijk om een algehele maat van de betrouwbaarheid te hebben. Daarom hebben we de empirische betrouwbaarheid (Zimowski, Muraki, Mislevy, & Bock, 2003) bij de totale steekproef en de kandidaatssteekproef berekend. De empirische betrouwbaarheid is gebaseerd op de ratio van de foutvariantie ten opzichte van de totale variantie, bij EAP-schattingen zoals gehanteerd bij de ACT Algemene Intelligentie geldt de volgende formule:

(5.1)

In deze formule (5.1) is ρ de betrouwbaarheid, σ² de ‘ware’ variantie en σ²_error de foutvariantie. De foutvariantie is te berekenen door voor iedere persoon in de steekproef het kwadraat van de berekende SEM te nemen, en vervolgens het gemiddelde hiervan over de gehele steekproef te nemen. De SEM of standaardfout geeft de spreiding aan die rondom de geschatte θ verwacht mag worden: dus hoe kleiner deze spreiding, hoe nauwkeuriger de meting. De ‘ware’ variantie, σ², is simpelweg de variantie van de geschatte θ’s uit de steekproef.

Naast de empirische betrouwbaarheid hebben we ook gekeken naar de gemiddelde SEM bij de totale steekproef en kandidaatssteekproef: zoals hierboven aangegeven is de SEM echter afhankelijk van waar op de θ-schaal gemeten wordt, vandaar dat we ook de SEM’s afgezet hebben tegen θ.

5.2. Betrouwbaarheid

5.2.1. Empirische betrouwbaarheid

De empirische betrouwbaarheid is berekend voor de subtests in de totale steekproef en de kalibratiesteekproef. In Tabel 5.1. zijn de varianties van de θ’s en hun bijbehorende errorvarianties weergegeven. Hiermee is, zoals hierboven beschreven, de empirische betrouwbaarheid te berekenen; deze zijn weergegeven in de laatste kolom van Tabel 5.1. De Figurenreeksen als voorbeeld nemend: de variantie van de θ’s is .763 en de errorvariantie is .234. De empirische betrouwbaarheid komt dus overeen met .763 / (.763-.234) = .77.

Tabel 5.1. Empirische betrouwbaarheid.
	Totale steekproefa				Kandidaatssteekproefb
	Variantie θ	Error variantie	EB		Variantie θ	Error variantie	EB
Cijferreeksen	.837	.163	.84		.713	.137	.84
Figurenreeksen	.763	.234	.77		.720	.167	.81
Verbale Analogieën	.884	.116	.88		.699	.098	.88
g-score	.629	.064	.91		.498	.041	.92
Noot. EB = empirische betrouwbaarheid.   a N = 6277, b N = 2532.

 

Bij de totale steekproef zijn de betrouwbaarheden van de subtests Cijferreeksen en Verbale Analogieën voldoende tot ruim voldoende, wanneer afgezet tegen de richtlijnen van de Cotan (2009; < .80 onvoldoende, .80 ≤ r ≤ .90 voldoende, r ≥ .90 goed). De betrouwbaarheid van de g-score is goed: en hierbij moet dus de kanttekening geplaatst worden dat dit een soort gemiddelde maat is die specifieke betrouwbaarheden afhankelijk van de θ-schaal verbloemen (Brown, 2014). Bovendien zaten er in de kalibratiesteekproef (onderdeel van de totale steekproef) ook personen die maar een zeer klein aantal items hadden gemaakt: per definitie zal de SEM bij deze personen hoger zijn, wat invloed gehad zal hebben op deze algehele betrouwbaarheidsmaat (zie volgende sectie). Voor veel voorkomende waarden van θ (ongeveer tussen -1 en 1) zal de betrouwbaarheid goed zijn (zie volgende sectie en Figuur 5.1. en 5.2.).

Bij deze resultaten moet een belangrijke opmerking gemaakt worden: de g-score voor de totale steekproef komt al overeen met de criteria voor een ‘goede’ betrouwbaarheid (> .90) van de Cotan (2009). Deze betrouwbaarheden zijn echter ook gebaseerd op responses uit de kalibratiesteekproef waar respondenten een subset van items lineair en niet adaptief – dus niet geënt op hun niveau – kregen. In de adaptieve test zijn de items wel gericht op iemands niveau waardoor de metingen nauwkeuriger zijn (zie rechterkant van Tabel 5.1) en de betrouwbaarheid dus hoger: de betrouwbaarheid van de g-score bij de adaptieve test is met .92 goed te noemen. De betrouwbaarheden van de subtests zijn ook relatief hoog (gemiddeld .84 en dus >.80, ‘voldoende’).

De betrouwbaarheid van Figurenreeksen komt net boven de richtlijn van .80 die de Cotan (2009) aanhoudt voor een ‘voldoende’ beoordeling voor tests op basis waarvan belangrijke beslissingen genomen worden – zoals het afwijzen of aannemen van een kandidaat in selectiesituaties. De scores op de drie subtests zouden dis eventueel – wanneer de situatie hierom vraagt, bijvoorbeeld wanneer het werk waarvoor geselecteerd wordt een sterk numerieke component kent – ook hiervoor gebruikt kunnen worden, aangezien de betrouwbaarheden van deze tests als ‘voldoende’ beoordeeld kunnen worden. Echter, omdat het hier niet om een ‘goede’ betrouwbaarheid gaat, en gezien het meetdoel en praktisch doel van de ACT Algemene Intelligentie (werkprestaties voorspellen), adviseren we belangrijke beslissingen – zoals in selectiesituaties – te nemen op basis van de g-score (zie Hoofdstuk 1, sectie 1.3.2.).

5.2.2. SEM-waarden

Ook hebben we de gemiddelde SEM-waarden voor de twee steekproeven berekend. Deze zijn weergegeven in Tabel 5.2. De SEM van de g-score wordt berekend door de informatie (= 1/SEM²) geleverd door de drie subtests op te tellen en hiermee weer de SEM te berekenen (= 1/√Info).

Tabel 5.2. Nauwkeurigheid van θ-schatting.
	Totale steekproefa		Kandidaatssteekproefb
	Gem. SEM		Gem. SEM
Cijferreeksen	.39		.37
Figurenreeksen	.46		.41
Verbale Analogieën	.33		.31
g-score	.25		.20
a N = 6277, b N = 2532.

 

In Tabel 5.2 zien we hetzelfde patroon als in Tabel 5.1.: de betrouwbaarheden zijn voldoende tot goed, waarbij Figurenreeksen de laagste betrouwbaarheid laat zien en Verbale Analogieën de hoogste.

In de kandidaatssteekproef zijn de betrouwbaarheden nog iets hoger (te zien aan lagere gemiddelde SEM-waarden). De betrouwbaarheid van de g-score is zeer hoog te noemen met een zeer lage gemiddelde SEM-waarde van .20.

5.2.3. Betrouwbaarheid bij verschillende groepen

Om te onderzoeken of de ACT Algemene Intelligentie even betrouwbaar meet bij verschillende subgroepen (mannen/vrouwen, allochtonen/autochtonen, laag/midden/hoog opleidingsniveau, jong/middelbaar/oud) is voor deze subgroepen afzonderlijk de betrouwbaarheid berekend op basis van de gemiddelde SEM. Voor afzonderlijke groepen is empirische betrouwbaarheid minder bruikbaar: zoals de formule hierboven al aanduidt, speelt de variantie van de geschatte scores een belangrijke rol in de berekening hiervan. Bij een constant gehouden foutvariantie (σ²_error), zorgt een kleinere variantie van de geschatte θ’s (σ²) automatisch voor een lagere betrouwbaarheid. En omdat subgroepen homogener zijn dan de totale populatie, zullen de varianties van de ware scores bij de subgroepen per definitie lager zijn (een vorm van restriction of range). Denk bijvoorbeeld aan groepen van verschillende opleidingsniveaus: in acht nemend dat intelligentie normaal verdeeld is over de gehele populatie, zal de WO-groep aan het rechteruiteinde van de verdeling zitten waardoor de variantie van deze groep beperkt wordt. MBO-ers, die in het midden van de verdeling zitten, hebben dit probleem niet. Daarom zijn alleen betrouwbaarheden op basis van de gemiddelde SEM-waarden (1-SEM² ) weergegeven in Tabel 5.3. (totale steekproef) en Tabel 5.4. (kandidaatssteekproef).

Tabel 5.3. Nauwkeurigheid van θ-schatting bij geslacht, leeftijd, opleidingsniveau en etniciteit in totale steekproef – gemiddelde SEM.
	Geslachta		Leeftijdb			Opleidingc			Etniciteitd
	Man	Vrouw	Laag	Midden	Hoog	Laag	Midden	Hoog	Autochtoon	Allochtoon
Cijferreeksen	.83	.83	.84	.84	.81	.86	.81	.81	.83	.82
Figurenreeksen	.78	.73	.76	.76	.72	.77	.72	.71	.70	.69
Verbale Analogieën	.88	.88	.89	.88	.87	.85	.86	.86	.87	.86
g-score	.91	.90	.91	.91	.89	.90	.89	.88	.89	.89
a Subtests: Nmannen = 2461-2591, Nvrouwen = 2142-2332, g-score: Nmannen = 3020, Nvrouwen = 2941.   b Subtests: Nlaag = 477-505, Nmidden = 1754-1872, Nhoog = 1970-2143, g-score: Nlaag = 596, Nmidden = 2207, Nmidden = 2755. c Subtests: Nlaag = 723-1027, Nmidden = 2209-2344, Nhoog = 1328-1479, g-score: Nlaag = 1286, Nmidden = 2838,                    Nmidden = 1629. d Subtests: Nautochtoon = 2275-2550, Nallochtoon = 378-421, g-score: Nautochtoon = 3474, Nallochtoon = 535.

Tabel 5.4. Nauwkeurigheid van θ-schatting bij geslacht, leeftijd, opleidingsniveau en etniciteit in kandidaatssteekproef – gemiddelde SEM.
	Geslachta		Leeftijdb			Opleidingc				Etniciteitd
	Man	Vrouw	Laag	Midden	Hoog	VMBO	MBO	HBO	WO	Aut.	Allocht.
Cijferreeksen	.83	.84	.83	.84	.79	.76	.78	.80	.82	.81	.81
Figurenreeksen	.81	.81	.82	.82	.78	.75	.78	.77	.77	.90	.88
Verbale Analogieën	.88	.88	.90	.89	.88	.87	.87	.80	.75	.74	.74
g-score	.92	.93	.93	.93	.91	.89	.90	.87	.87	.90	.89
a Nmannen = 1463, Nvrouwen = 771-773.   b Nlaag = 260, Nmidden = 933, Nhoog = 640. c NVMBO = 204, NMBO = 1094-1095, NHBO = 402, NWO = 327. d Nautochtoon = 194, Nallochtoon = 90.

Meer informatie over de indeling in de categorieën is te vinden in Hoofdstuk 6, sectie 6.8. Bij de totale steekproef zijn de verschillen in betrouwbaarheden tussen mannen en vrouwen klein. Belangrijk is ook dat verschillen tussen autochtonen en allochtonen klein zijn: voor autochtonen en allochtonen kan met de ACT Algemene Intelligentie even betrouwbaar de specifieke aspecten van intelligentie en algemene intelligentie gemeten worden. Hetzelfde geldt voor de drie leeftijdscategorieën.

De verschillen bij opleidingsniveau zijn bij de totale steekproef iets groter, waarbij het verschil vooral zichtbaar is bij Cijferreeksen en Figurenreeksen. Bij beide subtests zijn de metingen betrouwbaarder bij een lager opleidingsniveau. Dit resultaat is goed te verklaren wanneer we naar Figuur 5.1 kijken: we hadden al geconcludeerd dat de itembanken van Cijferreeksen en Figurenreeksen de meest informatieve items bevatten rond wat lagere θ-waarden. Dit zorgt ervoor dat metingen bij Cijferreeksen en Figurenreeksen betrouwbaarder zijn bij een lagere θ (en dus lager opleidingsniveau): daar bevinden zich simpelweg meer ‘betere’, meer informatieve items die meer informatie geven over iemands intelligentie. Echter, uit Tabel 5.4 blijkt dat dit niet tot minder nauwkeurige schattingen van θ leidt bij mensen met hogere θ’s (namelijk met hogere opleidingsniveaus).

Interessant om op te merken is dat in de kandidaatssteekproef bij Cijferreeksen de betrouwbaarheid juist wat hoger is bij hoger opgeleiden (WO) dan bij lagere opleidingsniveaus. Bij de totale steekproef zagen we geen verschillen op Verbale Analogieën naar opleiding, terwijl we bij de kandidaatssteekproef zien dat de meting wat nauwkeuriger is bij lager opgeleiden. Mogelijke oorzaken voor verschillen tussen de totale steekproef en kandidaatssteekproef zijn de manier van afname (lineair versus adaptief), of verschillen in varianties van de onderzochte groepen.

Er zijn nauwelijks verschillen in betrouwbaarheden bij de g-scores gevonden bij de totale steekproef. Hetzelfde geldt voor de kandidaatssteekproef (die de volledig adaptieve ACT Algemene Intelligentie hebben voltooid).

5.2.4. Betrouwbaarheid bij normgroepen

In Tabel 5.5 zijn de betrouwbaarheden weergegeven van de normgroepen van de ACT Algemene Intelligentie (zie hoofdstuk ‘Normen’).

Tabel 5.5 Nauwkeurigheid van θ-schatting bij de normgroepen VMBO, MBO, HBO, WO en Beroepsbevolking.
	VMBO	MBO	HBO	WO	Beroepsbevolking
Cijferreeksen	.76	.78	.81	.81	.84
Figurenreeksen	.73	.79	.78	.77	.82
Verbale Analogieën	.88	.87	.81	.73	.89
g-score	.89	.91	.88	.85	.93

Zoals eerder beschreven adviseren wij (selectie)beslissingen te nemen op basis van de g-scores en de subtest scores voornamelijk te gebruiken voor nadere duiding. Afgezet tegenover de gehanteerde richtlijnen van de COTAN voor tests voor belangrijke beslissingen (< .80 onvoldoende, .80 ≤ r ≤ .90 voldoende, r ≥ .90 goed) kunnen bovenstaande gegevens voor VMBO en HBO als ‘voldoende’ beschouwd worden (de waarden zitten immers dicht tegen de .90 aan), de MBO- en Beroepsbevolking score een ‘goed’, en de WO score een ‘voldoende’.

5.2.5. SEM-waarden afhankelijk van de θ-schaal

Zoals hiervoor al beschreven, zijn de hier besproken maten een soort gemiddelde maat van betrouwbaarheid, die één van de belangrijkste kenmerken van IRT (namelijk dat de betrouwbaarheid van de meting afhankelijk is van waar gemeten wordt op de θ-schaal) geen recht doet. Om meer inzicht te krijgen in waar de ACT Algemene Intelligentie precies (on)nauwkeurig zijn, zijn de geschatte scores van de kandidaatssteekproef afgezet tegen de SEM-waarden.

Figuur 5.1. θ en SEM-waarden bij de kandidaatssteekproef.

 

De horizontale lijnen geven een betrouwbaarheid van .85 (SEM = .39) en .80 (SEM = .45) aan. In lijn met de gemiddelde waarden zoals in de voorgaande secties beschreven zien we de laagste waarden bij Verbale Analogieën. Bij deze subtest zien we dat het meest nauwkeurig gemeten wordt bij een θ van ongeveer -0.5: dit is ook wat we mogen verwachten door de kenmerken van de itembank (zie Figuur 2.8. in Hoofdstuk 2). Dat wil zeggen: daar waar de meest informatieve items in de itembank zitten, daar wordt het meest nauwkeurig gemeten – en zijn de SEM-waarden dus het laagst.

Ook wanneer we de gevonden SEM-waarden bij Cijferreeksen en Figurenreeksen vergelijken met de itembanken zoals weergegeven in Figuur 2.2. en Figuur 2.5. dan zien we duidelijke parallellen. Het nauwkeurigst wordt gemeten bij lagere θ’s, waarbij de korte daling van de SEM’s rond een θ van 1 (bij Cijferreeksen sterker aanwezig dan bij Figurenreeksen) opvallend is. In overeenstemming met de algehele betrouwbaarheid van Figurenreeksen, zien we dat ook deze subtests de meeste SEM-waarden boven de .39 heeft. Bij zowel Cijferreeksen als Figurenreeksen wordt minder nauwkeurig gemeten bij hogere θ-waarden; echter, de meerderheid van de SEM-waarden ligt ook bij hogere niveaus nog onder de .39 wat ongeveer overeenkomt met een α van .85 (Cijferreeksen) of .45 wat overeenkomt met een α van .80 (Figurenreeksen).

In Figuur 5.2. zijn de geschatte g-scores afgezet tegenover de SEM-waarden gebaseerd op de gehele test.

Figuur 5.2. g-scores en SEM-waarden bij de kandidaatssteekproef.

De relatie tussen de geschatte g-score en de SEM is minder duidelijk dan bij de subtests: de laagste SEM’s worden wel gevonden bij lagere θ’s, maar er zijn ook hogere θ-waarden met lage SEM’s (en lagere θ’s met hoge SEM’s). De horizontale lijn geeft een SEM van .32 aan (α van .90): uit dit figuur blijkt dus duidelijk dat over de gehele linie, de ACT Algemene Intelligentie zeer betrouwbaar meet. Wanneer we Figuur 5.2. met Figuur 2.10. dan zien we weer duidelijke parallellen: de behaalde SEM’s zijn, zoals te verwachten, het laagst waar zich de meeste informatieve items vinden in de itembanken (rond -0.5). Omdat er relatief minder informatieve items zich bij hogere en lagere θ-waarden bevinden nemen de SEM waarden toe bij deze hogere en lagere hogere en lagere θ-waarden. Echter, zoals gezegd meet de ACT Algemene Intelligentie zeer betrouwbaar over de gehele θ-schaal.

Bovenstaande figuren tonen wel aan dat het in de toekomst noodzakelijk is dat er nauwkeuriger gemeten kan worden bij hogere θ-waarden bij de Cijferreeksen en Figurenreeksen-subtests: in de praktijk betekent dit dat we in de nabije toekomst nieuwe, moeilijkere, goed discriminerende items gaan ontwikkelen.

5.3. Algemene conclusies betrouwbaarheid

De in de dit hoofdstuk beschreven onderzoeken tonen aan dat de betrouwbaarheid van de subtests van de ACT Algemene Intelligentie voor relevante waarden van θ goed is. De bij de totale steekproef gevonden betrouwbaarheden waren voldoende tot goed, waarbij deze betrouwbaarheden deels niet verkregen waren bij een adaptief aangeboden test. De waarden die bij deze steekproef gevonden zijn, kunnen dus slechts beschouwd worden als een ondergrens van de betrouwbaarheid. De betrouwbaarheden bij de kandidaatssteekproef, die de test wel adaptief gemaakt hadden, waren dan ook goed te noemen, zowel op basis van de empirische betrouwbaarheid (gemiddeld .81 voor de subtests en .92 voor de g-score) als de gemiddelde SEM (gemiddeld .86 voor de subtests en .96 voor de g-score).

Ook waren de verschillen in betrouwbaarheden tussen verschillende subgroepen op basis van achtergrondkenmerken minimaal. Dit betekent dat de ACT Algemene Intelligentie bij verschillende groepen in de populatie even nauwkeurig meet en dus bij deze groepen goed bruikbaar is. Een punt van aandacht is echter dat er bij hogere niveaus enigszins minder nauwkeurig gemeten wordt (zie Figuur 5.1) bij de subtests Cijferreeksen en Figurenreeksen – bij de g-score is dit niet het geval.  In de toekomst zullen er daarom nieuwe items ontwikkeld worden om ook bij hogere θ’s nog nauwkeuriger te kunnen meten.

 

 

6. Begripsvaliditeit

6.1. Inleiding

De validiteit van een vragenlijst geeft een indicatie van de mate waarin het instrument daadwerkelijk het construct meet dat het pretendeert te meten. Bijvoorbeeld: meet een persoonlijkheidsvragenlijst ook daadwerkelijk persoonlijkheid? Of in het geval van de ACT Algemene Intelligentie geldt: meet de vragenlijst daadwerkelijk de intelligentie van een persoon?

In de literatuur worden verschillende soorten validiteit onderscheiden. Wij hanteren de klassieke driedeling: inhoudsvaliditeit, begripsvaliditeit en criteriumvaliditeit (Cotan, 2009). De inhoudsvaliditeit van de ACT Algemene Intelligentie heeft betrekking op de mate waarin de items representatief zijn voor het domein van cognitieve vaardigheid. Informatie over de inhoudsvaliditeit is te vinden in Hoofdstuk 1 en 2. Bij criteriumvaliditeit gaat het om de voorspellende waarde van testscores (Cotan, 2009). Informatie hierover is te vinden in Hoofdstuk 7.

De begripsvaliditeit geeft aan of de vragenlijst daadwerkelijk de constructen meet die het pretendeert te meten (Cotan, 2009). Er zijn verschillende manieren om bewijs te leveren voor begripsvaliditeit: bijvoorbeeld factoranalyse voor het aantonen van de unidimensionaliteit, het vergelijken van de gemiddelde scores van groepen waarvan men mag verwachten dat ze verschillen zullen vertonen en het berekenen van correlaties met tests die (ongeveer) hetzelfde zouden moeten meten (‘soortgenotenvaliditeit’, Cotan, 2009). Voor de ACT Algemene Intelligentie zijn al deze manieren, en meer gebruikt; in dit hoofdstuk zullen alle onderzoeken die bewijs leveren voor de begripsvaliditeit van de ACT Algemene Intelligentie worden besproken.

Opmerkingen bij dit hoofdstuk

We willen de lezer hier graag erop attent maken dat de onderzoeken in sectie 6.5.2. en 6.7. op grotendeels dezelfde steekproef uit de testpraktijk gebaseerd zijn. Deze onderzoeken (naar begrijpend lezen en reactietijden) zijn in verschillende secties besproken omdat elk van de onderzoeken toegespitst zijn op een iets andere vorm van begripsvaliditeit. Zo valt begrijpend lezen – en begrijpend lezen-tests – meer binnen het domein van intelligentie, waardoor we hier spreken van soortgenotenvaliditeit. Reactietijden en reactietijdtaken zijn meer perifeer aan intelligentie, daarom hebben we dit besproken onder de noemer convergente validiteit. De procedure en omstandigheden van het onderzoek worden alleen in sectie 6.5.2. toegelicht.

In dit hoofdstuk worden verschillende keren steekproeven vergeleken met de beroepspopulatie wat betreft hun representativiteit op basis van verschillende kenmerken (bijv. geslacht, leeftijd of etniciteit) door middel van χ²-toetsen. Daarom hebben we ook steeds naar de effectgrootten φ gekeken (bij achtergrondkenmerken met twee categorieën, zoals geslacht) en Cramer’s V (bij achtergrondkenmerken met >2 categorieën). Voor φ geldt de volgende vuistregel: .1 duidt op een klein effect, .30 op ene gemiddeld effect en .50 op een groot effect (Cohen, 1988). Voor Cramer’s V geldt dat de classificatie van het effect afhankelijk is van het aantal categorieën van de variabele: bij drie categorieën gelden .07, .21 en .35 als respectievelijk klein, gemiddeld en groot, bij vier categorieën respectievelijk .06, .17 en .29. In de tekst wordt steeds de grootte van het effect beschreven.

6.2. Item-fit

 De in sectie 1.5.1. besproken item-fitanalyse op basis van de Q₁ waarden en de fit-plots zeggen al iets over de validiteit van de ACT Algemene Intelligentie. Slechte item-fit is een indicatie dat de itemparameters bedenkelijke validiteit hebben: dit wil namelijk zeggen dat ze niet reflecteren hoe personen echt reageren op de items (Reise, 1990). En aangezien deze items (en dus hun parameters) worden gebruikt om θ te berekenen, zegt item-fit weer iets over de validiteit van θ, oftewel de meting van intelligentie.

Gebaseerd op de gestandaardiseerde residuen en Q₁– en Lz-waarden uit Hoofdstuk 1 kunnen we concluderen dat de item-fit voldoende is, oftewel dat de itemparameters realistisch en een goede beschrijving van de werkelijkheid zijn. Met andere woorden, de items lijken te reflecteren hoe personen echt reageren op de items, wat bijdraagt aan de validiteit van de items in het bijzonder en de ACT Algemene Intelligentie in het algemeen.

6.3. Interne structuur

In het herkalibratieonderzoek, waarin de a– en b-parameters geschat werden (zie sectie 1.8.), hebben we tevens de θ’s door IRTPRO laten bepalen (op basis van de EAP-methode). Hiermee hebben we de relatie met andere variabelen kunnen onderzoeken, wat informatie verschaft over de validiteit van de ACT Algemene Intelligentie.

Zoals aangegeven in sectie 1.8. is de itemkalibratie uitgevoerd op een gemengde steekproef (kalibratiesteekproef en kandidaatssteekproef afkomstig uit de Ixly-database). Daarom zullen in het vervolg alle resultaten voor deze totale steekproef besproken worden, alsook van de kandidaatssteekproef. Hier is voor gekozen omdat het in eerste instantie belangrijk is inzicht te krijgen in de psychometrische kwaliteiten van de items en scores bij de groep waarop de itemparameters op gebaseerd zijn. Echter, omdat in deze groep ook personen (namelijk die uit de kalibratiesteekproef) zitten die de test niet adaptief gemaakt hebben en de test onder andere omstandigheden hebben gemaakt dan ‘echte’ kandidaten, is het ook belangrijk inzicht te geven in de kenmerken van de test bij deze laatste groep personen. Directe gebruikers van de test zullen meer belang hechten aan de resultaten onder kandidaten die de test in selectiesituaties hebben gemaakt.

Allereerst wordt echter het onderzoek besproken dat gedaan is naar de unidimensionaliteit van de subtests van de ACT Algemene Intelligentie. Unidimensionaliteit is een belangrijke assumptie van IRT. Dat wil zeggen; IRT veronderstelt dat het gegeven antwoord op een item (of de correlatie tussen twee items van een zelfde test) volledig verklaard kan worden door één construct (bijvoorbeeld intelligentie) en niet door meerdere constructen (bijvoorbeeld intelligentie en leesvaardigheid). Omdat aan deze strenge assumptie in werkelijkheid moeilijk te voldoen is, wordt het aantonen van een aanzienlijke mate van unidimensionaliteit vaak als afdoende beschouwd.

6.3.1. Onderzoek naar de unidimensionaliteit van de subtests

 Een IRT-model is feitelijk een ‘normaal’ factormodel voor dichotome data, dus voor geobserveerde data die de waarden 0 en 1 aannemen (De Ayala, 2013). Het is daarom mogelijk om verschillende factormodellen (bijvoorbeeld een model met 1 factor of met 2 factoren) met elkaar te vergelijken.

Dit hebben we gedaan door IRTPRO een exploratieve factoranalyse te laten doen met één factor en met twee factoren.[1] Vervolgens hebben wij de fit van de modellen vergeleken op basis van de verschillen in de -2loglikelihood waarden (die χ²-verdeeld zijn en dus gebruikt kunnen worden voor hypothese-toetsing). Echter, omdat χ²-toetsen sterk beïnvloed worden door steekproefgrootte hebben wij ook gekeken naar de BIC-waarden van de modellen: lagere BIC-waarden duiden op een beter model. Bij het model met één factor is verder gekeken hoeveel items een lading van >.30 lieten zien: een lading van >.30 duidt erop dat het item gezien kan worden als indicator van de factor. Een andere manier om te kijken of er een dominante factor aanwezig is, is het beoordelen van de grootte van de eigenwaarden van de factoren: we kunnen spreken van unidimensionaliteit als de eerste eigenwaarde van de eerste factor (of component) gedeeld door het aantal items >.20 is (Templin, 2007). Echter, de schattingsmethode van IRTPRO levert geen eigenwaarden op. Hiervoor is de som van de gekwadrateerde ladingen gebruikt, wat grotendeels op hetzelfde neerkomt. Ook zijn de factorladingen bij het twee-factor model geïnspecteerd om te zien of er een patroon in de factorladingen te ontdekken was en om items op te sporen die afwijkende ladingen lieten zien.

De resultaten van de analyses zijn weergegeven in Tabel 6.1.

Tabel 6.1. Vergelijking modellen met één en twee factoren.
Model	Cijferreeksen			Figurenreeksen			Verbale Analogieën
	-2llh	Δ-2llh	BIC	-2llh	Δ-2llh	BIC	-2llh	Δ-2llh	BIC
1 factor	96904.26		100520.71			100538.07			93986.99
2 factoren	95495	1409.26	100911.11		681.05	101445.81		803.47	95002.31
Noot. -2llh = -2loglikelihood. Alle verschillen in -2loglikelihoodwaarden (Δ-2llh) waren significant (p < .001).

 

Cijferreeksen

De -2loglikelihoodwaarde van het model met één factor verschilde significant van de
-2loglikelihoodwaarde van het model met twee factoren (χ²-toets met 210 vrijheidsgraden, p < .001). Dit zou er op duiden dat een model met twee factoren een betere weergave van de werkelijkheid is. Echter, de BIC-waarde van het model met één factor was lager dan van het model met twee factoren. Deze waarden duiden aan dat het model met één factor beter is. Bovendien had 89% van de items een lading >.30, en was de som van de gekwadrateerde ladingen gedeeld door het aantal items .35: groter dan de drempelwaarde van .20 (Templin, 2007). Dit duidt op een voldoende mate van unidimensionaliteit.

Om inzicht te krijgen in de aard van de tweede factor zijn de factorladingen bekeken van de items op deze tweede factor. Het viel op dat het hier om items ging met eenzelfde soort logica – dus van een iets ander itemtype, die enigszins afwijken van de andere items.[2] Hoewel een model met één factor dus een redelijk goede weergave van de werkelijkheid was, was een eventuele tweede factor inhoudelijk goed te verklaren.

We kunnen verwachten dat het vinden van de logica van deze ‘afwijkende’ items verklaard kan worden door intelligentie. Dat wil zeggen, mensen met een hogere mate van intelligentie zullen eerder de ‘afwijkende’ logica kunnen ontdekken van deze items dan mensen met een lagere mate van intelligentie. Daarom hebben we ook een bifactormodel geschat (zie Figuur 6.2, sectie 6.4). In dit model worden itemresponses verklaard door één factor die alle itemresponses beïnvloedt (in dit geval intelligentie) en additionele factoren die itemspecifieke antwoorden beïnvloeden. Dit model verschilde significant van beide andere modellen op basis van de χ²-toets, terwijl de BIC-waarde van dit model (100681.21) lager was dan het twee-factor model, maar hoger dan het één-factor model. Qua fit lijkt dit model dus tussen het één- en twee-factor model in te liggen. Belangrijker is dat de ladingen op de algemene factor hoog waren, en op de specifieke factoren lager. Meer specifiek betekende dit dat 66% van de variantie door de algemene factor verklaard werd, de overige 34% door de overige specifieke factoren.[3] Wanneer gecontroleerd wordt voor itemspecifieke variantie dan zien we dus dat de itemresponses voor een belangrijk deel door de algemene factor verklaard kunnen worden.

Op basis van deze resultaten kunnen we concluderen dat de Cijferreeksentest een voldoende mate van unidimensionaliteit vertoont: de itemresponses lijken voldoende verklaard te kunnen worden door één factor.

Figurenreeksen

Ook bij de Figurenreeksen zagen we dat het twee-factoren model op basis van de χ²-toets beter leek dan het één-factor model (Δχ² = 681.05, df = 186), maar dat de BIC-waarde van het laatstgenoemde model lager (dus beter) was. In totaal hadden 73% van de items een lading van >.30, en de som van de gekwadrateerde ladingen gedeeld door het aantal items was >.20 (.25). Daarnaast lieten slechts 34% van de items een lading van >.30 zien op de tweede factor, waarbij deze factorladingen geen duidelijk patroon lieten zien. Bovendien was de som van de gekwadrateerde ladingen op de eerste factor bijna twee keer zo groot als de som van de gekwadrateerde ladingen op de tweede factor. Op basis van deze resultaten kunnen we concluderen dat Figurenreeksen unidimensionaliteit vertoont.

Verbale Analogieën

Tot slot zagen we ook bij Verbale Analogieën dat de BIC-waarde van het model met één factor lager was dan het model met twee factoren, waarbij het verschil in χ²-waarden significant was (Δχ² = 803.47, df = 213). Er bleek duidelijk sprake van unidimensionaliteit: maar liefst 93% van de items lieten een lading zien van >.30 op de eerste factor en de som van de gekwadrateerde ladingen gedeeld door het aantal items was >.20 (.43). De som van de gekwadrateerde ladingen op de eerste factor was meer dan 3½ keer zo groot als de som van de gekwadrateerde ladingen op de tweede factor.

Conclusie

Op basis van de hiervoor beschreven resultaten kan geconcludeerd worden dat de subtests van de ACT Algemene Intelligentie unidimensionaliteit vertonen. Dit is belangrijk omdat unidimensionaliteit een belangrijke assumptie van IRT is. Ook is het belangrijk voor de begripsvaliditeit van de ACT Algemene Intelligentie: het betekent namelijk dat de gegeven antwoorden verklaard lijken te worden door één construct (bijvoorbeeld ‘verbale intelligentie’ bij Verbale Analogieën) en relatief vrij is van andere, externe factoren – die we niet met de subtests willen meten – die de antwoorden beïnvloeden.

6.3.2. Onderzoek naar de psychometrische kwaliteit van de items

 De nauwkeurigheid van de itemparameterschattingen kan beoordeeld worden door te kijken naar de relatie tussen de standaardfout van de moeilijkheidsparameter – se(b_i) – en de standaarddeviatie van de θ-verdeling van de kalibratiepopulatie – sd(θ). Hierbij zou moeten gelden dat: se(b_i) < c*sd(θ), waarbij c een constante is. De Cotan (2009) hanteert de volgende richtlijnen:

• c ≥ 0.5 = groot (‘onvoldoende’)
• 3 ≤ c ≤ 0.4 = matig (‘voldoende’)
• c ≤ 0.2 = klein (‘goed’)

In het bovenstaande rijtje zijn er een aantal waarden voor c die niet ingedeeld kunnen worden, namelijk 0.2 ≤ c ≤ 0.3 en 0.4 ≤ c ≤ 0.5. Daarom hebben wij de volgende indeling gehanteerd:

• c ≥ 0.5 = groot (‘onvoldoende’)
• 4 ˂ c ˂ 0.5 = matig/groot
• 3 ≤ c ≤ 0.4 = matig (‘voldoende’)
• 2 ˂ c ˂ 0.3 = matig/klein
• c ≤ 0.2 = klein (‘goed’)

Om de kwaliteit van de items te beoordelen zijn de c-waarden bij de items van de ACT Algemene Intelligentie berekend. Het percentage items in elke categorie voor iedere subtest is weergegeven in Tabel 6.2.

Tabel 6.2. Percentage items in verschillende categorieën c-waarden voor standaardfouten b-parameters.
	>0.5	0.4 ˂ c ˂ 0.5	0.3 ≤ c ≤ 0.4	0.2 ˂ c ˂ 0.3	c ≤ 0.2
	groot	matig/groot	matig	matig/klein	klein
Cijferreeksen	10a	5	6	9	70
Figurenreeksen	26 a	3	7	11	54
Verbale Analogieën	8 a	2	6	11	72
Gemiddeld	15	3	6	10	65
a Het grootste gedeelte van deze items (83% voor Cijferreeksen en Figurenreeksen, 81% voor Verbale Analogieën) was nog nooit getoond in de adaptieve test. Zie tekst.

De meeste items bevinden zich in de categorieën met de kleinste standaardfouten voor de b-parameters. In de laagste twee categorieën (0.2 ˂ c ˂ 0.3 en c ≤ 0.2) bevinden zich voor Cijferreeksen, Figurenreeksen en Verbale Analogieën respectievelijk 79%, 65% en 83% van de items. Gemiddeld over de gehele test bevinden 75% van de items zich in deze twee categorieën.

Voor Cijferreeksen en Verbale Analogieën zijn de aantallen in de hoogste categorie (c ≥ 0.5) met 10% en 8% acceptabel te noemen. Dat wil zeggen; op itembanken van >100 items is de kans uitermate klein dat één van deze items getoond wordt. De kans op het krijgen van meerdere van deze items is nog veel kleiner: bij Verbale Analogieën is het krijgen van twee van deze items slechts 0.58%, en drie van deze items 0.04%. Dit is één van de redenen geweest om deze items toch in de itembanken te laten.

Maar de belangrijkste reden om de items in de itembanken te laten, was de verklaring voor waarom de standaardfouten groter waren voor bepaalde items: dit bleek namelijk bijna volledig te verklaren te zijn door het aantal keer dat een item getoond was in de echte, adaptieve test (versus alleen in het kalibratieonderzoek). Van de 12 items uit de Cijferreeksen itembank met c > 0.5 waren er 10 (83%) nooit getoond in de adaptieve test – dit betekent dat ze alleen aan de deelnemers in het kalibratieonderzoek getoond waren. De overige twee items waren 25 keer en 61 keer getoond in de adaptieve test, wat relatief weinig is gezien het feit dat er ongeveer 2500 kandidaten uit de Ixly database (dus die de test adaptief hebben gemaakt) in de totale kalibratiesteekproef zaten. Hetzelfde was het geval bij Verbale Analogieën: van de 16 items met c > 0.5 waren er 13 (81%) nooit aan kandidaten getoond. De overige drie items waren slechts 2, 9 en 14 keer getoond aan kandidaten.

Het percentage items in de hoogste categorie bij Figurenreeksen is in eerste instantie zorgwekkend (26%), maar ook hier gold weer dat het aantal keer dat het item in de ‘echte’ test gemaakt was de oorzaak leek. Van de 30 items met c > 0.5 waren er 25 (83%) nooit aan kandidaten getoond. De overige vijf items waren 1 (3 items), 3 en 4 keer getoond aan kandidaten.

Omdat de grootte van de standaardfouten dus vooral leek samen te hangen met het aantal keer dat de items in de daadwerkelijke adaptieve test getoond waren, hebben we de besloten deze te behouden en te heronderzoeken wanneer er meer data verzameld is bij de ACT Algemene Intelligentie. De verwachting is dat de standaardfouten dan wel aan de gestelde eisen zullen voldoen.

 Een andere belangrijke bevinding die we deden is dat de standaardfouten met name groter waren voor hogere b-waarden, een veel voorkomende bevinding in de literatuur (zie bijvoorbeeld Thissen en Wainer, 1982). Dit bleek uit de relatief hoge correlaties tussen de standaardfouten en de b-waarden; .68, .78 en .69 voor respectievelijk Cijferreeksen, Figurenreeksen en Verbale Analogieën. Hier speelt ook weer de N per item een rol: gezien het feit dat minder personen in de populatie een hogere θ hebben (ten opzichte van bijvoorbeeld personen met een gemiddelde θ), zullen minder mensen dit item te zien krijgen. Het is dus moeilijker om over deze items informatie te krijgen waardoor de standaardfouten van deze items relatief groot zijn.

Een andere manier om naar de kwaliteit van de items te kijken is om naar de c-waarden te kijken over de gehele itembanken. Voor Cijferreeksen, Figurenreeksen en Verbale Analogieën waren de gemiddelde c-waarden respectievelijk .27 (matig/klein), .48 (matig/groot) en .20 (klein). Echter, zoals in de vorige alinea beschreven, waren de hogere standaardfouten vooral te vinden bij hogere b-waarden. Omdat het hier dus gaat om een verdeling met enkele uitschieters hebben we ook de mediaan van de c-waarden berekend. De medianen van de c-waarden waren klein, respectievelijk .13, .16 en .11 voor Cijferreeksen, Figurenreeksen en Verbale Analogieën.

Conclusies

De kwaliteit van de items van de drie subtests van de ACT Algemene Intelligentie lijkt, op basis van de standaardfouten van de b-waarden, redelijk te zijn: voor Cijferreeksen, Figurenreeksen en Verbale Analogieën bevonden zich respectievelijk 79%, 65% en 83% in de ‘beste’ categorieën met de laagste standaardfoutwaarden. Er bevonden zich nog wel relatief veel items in de hoogste categorie, voornamelijk bij Figurenreeksen, maar dit leek met name te verklaren te zijn door het aantal keer dat het item getoond is, de hoogte van de b-waarde of een combinatie van beide.

De resultaten uit het bovenstaande onderzoek staan niet op zichzelf; de psychometrische kwaliteit van de items dient in combinatie met de resultaten uit de rest van dit hoofdstuk (en feitelijk ook uit Hoofdstuk 7, Criteriumvaliditeit) beoordeeld te worden. Al deze resultaten in ogenschouw nemend lijkt de psychometrische kwaliteit van de items voldoende. Wel zullen de standaardfouten van de b-waarden in de toekomst, wanneer er meer data verzameld is, heronderzocht worden.

6.3.3. Intercorrelaties subtests ACT Algemene Intelligentie

In de voorgaande secties hebben we gekeken naar de structuur van de items op subtestniveau. De ACT Algemene Intelligentie is gebaseerd op het idee dat een algemene intelligentiefactor, g, de scores op de subtests beïnvloedt. Daarom is het ook belangrijk te kijken naar de structuur op een hoger niveau, dus naar de relaties tussen de subtests.

Aangezien alle drie de subtests tot het domein intelligentie behoren kunnen we positieve correlaties verwachten tussen de scores gebaseerd op deze drie tests. Gezien de veronderstelde g-factor en op basis van eerdere bevindingen (Jensen, 1998) mogen we sterke onderlinge correlaties verwachten (r > .50).

De correlaties tussen de θ’s gebaseerd op de drie subtests zijn weergegeven in Tabel 6.3. De correlaties onder de diagonaal zijn gebaseerd op de totale gemengde steekproef, boven de diagonaal op de kandidaatssteekproef.

Tabel 6.3. Intercorrelaties subtests ACT Algemene Intelligentie in totale steekproef en kandidaatssteekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.59g	.56h	.84j
Figurenreeksen	.57a	1	.57i	.80k
Verbale Analogieën	.53b	.57c	1	.88l
g-score	.84d	.79e	.90f	1
Noot. Alle correlaties zijn significant bij een α van .01.
a N = 4046, b N = 3863, c N = 3724, d N = 5231, e N = 5092, f N = 4909.
g N = 2531, h N = 2529, i N = 2530, j N = 2531, k N = 2532, l N = 2530.

De correlaties zijn hoog, en ongeveer van een grootte die we op basis van de in de literatuur gevonden relaties tussen subtests binnen het domein intelligentie mogen verwachten (zie bijvoorbeeld Chabris, 2007). De correlaties bij de kandidaatssteekproef zijn vrijwel identiek aan de correlaties in de totale steekproef.

Deze bevindingen bieden het eerste bewijs voor de g-factor (zie Hoofdstuk 1): het feit dat de scores op basis van de drie tests sterk met elkaar correleren suggereert dat deze scores gedreven worden door één algemene factor. Om dit te onderzoeken is er een principale component analyse gedaan op deze drie scores. Er kwam in beide steekproeven overduidelijk één factor naar voren, die maar liefst 70.9% (totale steekproef) en 71.5% (kandidaten) van de variantie verklaarde. De ladingen op deze factor waren respectievelijk .85, .84 en .84 (totaal) en .85, .85, .84 (kandidaten) voor Cijferreeksen, Figurenreeksen en Verbale Analogieën. Dit biedt bewijs voor het veronderstelde theoretisch model van de ACT Algemene Intelligentie.

Om de begripsvaliditeit van de ACT Algemene Intelligentie verder te onderzoeken hebben we gekeken naar de intercorrelaties van de drie subtests bij verschillende groepen (namelijk op basis van geslacht, etniciteit, leeftijd en opleidingsniveau). Als de factorstructuur verschilt tussen bijvoorbeeld mannen en vrouwen dan heeft dit negatieve consequenties voor de interpretatie van de resultaten wanneer we mannen en vrouwen vergelijken op hun scores (gebrek aan meetinvariantie). Als de factorstructuur bij deze groepen gelijk is dan mogen we verwachten dat er geen verschillen in de hoogte van de onderlinge correlaties tussen de subtests zijn. Deze specifieke hypothese wordt hieronder voor elk van de achtergrondvariabelen getoetst.

6.3.4. Intercorrelaties bij verschillende groepen

6.3.4.1. Mannen en vrouwen

In Tabel 6.4. en 6.5. staan onder de diagonaal de intercorrelaties tussen de subtests voor mannen weergegeven, boven de diagonaal vrouwen.

Tabel 6.4. Intercorrelaties subtests ACT Algemene Intelligentie bij mannen en vrouwen – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.55g	.51h	.84j
Figurenreeksen	.57a	1	.56i	.77k
Verbale Analogieën	.53b	.57c	1	.90l
g-score	.84d	.79e	.89f	1
Noot. Alle correlaties zijn significant bij een α van .01.
a N = 2084, b N = 2032, c N = 1954, d N = 2591, e N = 2513, f N = 2461.
g N = 1657, h N = 1533, i N = 1467, j N = 2332, k N = 2266, l N = 2142.

Tabel 6.5. Intercorrelaties subtests ACT Algemene Intelligentie bij mannen en vrouwen – kandidaatssteekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.61	.57	.84
Figurenreeksen	.58	1	.61	.82
Verbale Analogieën	.55	.55	1	.88
g-score	.83	.79	.88	1
Noot. Alle correlaties zijn significant bij een α van .01.
Nmannen = 1463, Nvrouwen = 771-773.

Zo op het eerste oog valt al op dat de correlaties weinig van elkaar verschillen. Een formele statistische toets voor het verschil in correlaties (Cohen & Cohen, 1983) na r naar Z-transformaties wees uit dat alleen de correlatie tussen Cijferreeksen en de g-score bij de totale steekproef significant verschilde (Z = 2.14, p = .03, zie Tabel 6.4), maar in absolute zin was dit verschil zeer klein (Δr = .02). Bij de kandidaatssteekproef werd dit verschil ook gevonden (Z = 2.10, p = .04, zie Tabel 6.5), en ook werd er een verschil gevonden voor de correlatie tussen Figurenreeksen en Verbale Analogieën (Z = 2.22, p = .03). Echter, ook hier was het absolute verschil klein (.06).

Bij beide groepen toonde een principale component analyse aan dat er één duidelijke component was; in de kalibratiesteekproef verklaarde deze bij mannen 70.6% van de variantie, bij vrouwen 71.1%. De ladingen waren bij zowel de mannen als vrouwen gemiddeld .84 in deze steekproef. Bij de kandidaatssteekproef was de verklaarde variantie van de g-factor 70.7% bij mannen en 73.2% bij vrouwen, met gemiddelde ladingen van .84 (mannen) en .86 (vrouwen)).
6.3.4.2. Intercorrelaties autochtonen en allochtonen

 Dezelfde analyses hebben we gedaan voor autochtonen en allochtonen. Zoals uitgelegd in sectie 6.8.4. zijn er op dit moment drie verschillende steekproeven waarin we informatie hebben over etniciteit en waar we dus vergelijkingen tussen autochtonen en allochtonen kunnen maken.

De eerste is de kalibratiesteekproef. De tweede is een steekproef uit de Ixly database (N = 284), verzameld tussen juli en november 2016. De derde is een samengestelde steekproef uit de eerste en tweede steekproef.

Kalibratiesteekproef

In Tabel 6.6. staan onder de diagonaal de intercorrelaties van de subtests voor autochtonen en boven de diagonaal voor allochtonen voor de kalibratiesteekproef.

Tabel 6.6. Intercorrelaties subtests ACT Algemene Intelligentie bij autochtonen en allochtonen – kalibratiesteekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.58g	.47h	.84j
Figurenreeksen	.49a	1	.57i	.79k
Verbale Analogieën	.45b	.49c	1	.91l
g-score	.84d	.75e	.90f	1
Noot. Alle correlaties zijn significant bij een α van .01.
a N = 1324, b N = 1157, c N = 1049, d N = 2356, e N = 2248, f N = 2081, g N = 181, h N = 174, i N = 138, j N = 331, k N = 295, l N = 288.

In deze steekproef bleek dat de correlaties niet significant van elkaar verschilden tussen de twee groepen. Een principale component analyse toonde aan dat er één component was die de relaties verklaarde, bij autochtonen verklaarde deze 58.5% van de variantie, bij allochtonen 59.2%. De ladingen op deze component waren nagenoeg gelijk aan elkaar bij de twee groepen en hoog (gemiddeld ongeveer .75).

Steekproef uit Ixly database

De intercorrelaties bij de steekproef uit de Ixly database zijn weergegeven in Tabel 6.7.

Tabel 6.7. Intercorrelaties subtests ACT Algemene Intelligentie bij autochtonen en allochtonen – Ixly database.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.46	.49	.78
Figurenreeksen	.54	1	.41	.71
Verbale Analogieën	.47	.45	1	.86
g-score	.79	.76	.85	1
Noot. Alle correlaties zijn significant bij een α van .01   Nautochtonen = 194 en Nallochtonen = 90.

In deze steekproef bleek eveneens dat de correlaties niet significant van elkaar verschilden tussen de twee groepen. Een principale component analyse toonde aan dat er één component was die de relaties verklaarde, bij autochtonen verklaarde deze 65.7% van de variantie, bij allochtonen 63.6%. De ladingen op deze component waren nagenoeg gelijk aan elkaar bij de twee groepen en hoog (gemiddeld ongeveer .80).

Totale steekproef

Tot slot zijn de intercorrelaties bij de totale, gemengde steekproef weergegeven in Tabel 6.8.

Tabel 6.8. Intercorrelaties subtests ACT Algemene Intelligentie bij autochtonen en allochtonen – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.55g	.47h	.83j
Figurenreeksen	.50a	1	.51i	.78k
Verbale Analogieën	.45b	.50c	1	.90l
g-score	.84d	.75e	.89f	1
Noot. Alle correlaties zijn significant bij een α van .01
a N = 1518, b N = 1351, c N = 1243, d N = 2550, e N = 2442, f N = 2275, g N = 271, h N = 264, i N = 228, j N = 421, k N = 385, l N = 378.

Ook in deze steekproef bleek dat de correlaties niet significant van elkaar verschilden tussen de twee groepen. Een principale component analyse toonde aan dat er één component was die de relaties verklaarde, bij autochtonen verklaarde deze 71.4% van de variantie, bij allochtonen 62.5%. De ladingen op deze component waren nagenoeg gelijk aan elkaar bij de twee groepen en hoog (gemiddeld ongeveer .79).

6.3.4.3. Intercorrelaties naar leeftijd

 Totale steekproef

 In Tabel 6.9 staan onder de diagonaal de intercorrelaties van de subtests voor mensen uit de laagste leeftijdscategorie (15 tot 25) en boven de diagonaal voor mensen uit de middelste leeftijdscategorie (25 tot 44). In Tabel 6.10 zijn de intercorrelaties weergegeven voor mensen uit de hoogste leeftijdscategorie (45 tot en met 65).

Tabel 6.9. Intercorrelaties subtests ACT Algemene Intelligentie bij lage (15 tot 25) en middelbare leeftijd (25 tot 45) – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.57g	.58h	.86j
Figurenreeksen	.58a	1	.58i	.78k
Verbale Analogieën	.56b	.58c	1	.90l
g-score	.85d	.77e	.91f	1
Noot. Alle correlaties zijn significant bij een α van .01
a N = 404, b N = 386, c N = 376, d N = 505, e N = 495, f N = 477, g N = 1457, h N = 1419, i N = 1339, j N = 1872, k N = 1792, l N = 1754.

  

Tabel 6.10. Intercorrelaties subtests ACT Algemene Intelligentie bij hoge leeftijd (45 tot 65) – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1
Figurenreeksen	.52a	1
Verbale Analogieën	.43b	.52c	1
g-score	.82d	.77e	.89f	1
Noot. Alle correlaties zijn significant bij een α van .01
a N = 1477, b N = 1358, c N = 1304, d N = 2143, e N = 2089, f N = 1970.

 

In deze steekproef verschilden de correlaties niet significant van elkaar tussen de laagste en middelste leeftijdscategorieën. De correlatie tussen Cijferreeksen en Verbale Analogieën verschilde significant (Z = 3.05, p = .00) tussen de laagste (r = .56) en hoogste leeftijdscategorie (r = .43). Ook het verschil in de correlatie tussen Cijferreeksen en de g-score was significant (Z = 2.41, p = .02), hoewel in absolute zin klein (Δr = .03).

Tussen de middelste en de hoogste leeftijdscategorieën vonden we wat meer verschillen. De Cijferreeksen-Verbale Analogieën relatie liet het grootste verschil zien (Δr = .15, Z = 5.39, p = .00). Hoewel de correlaties Figurenreeksen-Verbale Analogieën (Z = 2.07, p = .04), Cijferreeksen-g-score (Z = 4.46, p = .00) en Verbale Analogieën-g-score (Z = 2.21, p = .03) significant van elkaar verschilden, waren deze verschillen in absolute zin zeer klein (respectievelijk Δr = .06, Δr = .04 en Δr = .01).

 Een principale component analyse toonde aan dat er één component was die de relaties tussen de subtests verklaarde, respectievelijk verklaarde deze 72.8%, 72.9% en 67.2% van de variantie bij personen uit de laagste, middelste en hoogste leeftijdscategorie. De ladingen op deze component waren nagenoeg gelijk aan elkaar (.85 bij laag/midden, .82 bij hoog).

 Kandidaatssteekproef

 In Tabel 6.11 staan onder de diagonaal de intercorrelaties weergegeven voor jongeren (15 tot 25) en boven de diagonaal voor mensen met een middelbare leeftijd (25 tot 45).

Tabel 6.11. Intercorrelaties subtests ACT Algemene Intelligentie bij lage (15 tot 25) en middelbare leeftijd (25 tot 44) – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.61	.61	.84
Figurenreeksen	.61	1	.61	.81
Verbale Analogieën	.64	.59	1	.90
g-score	.85	.79	.92	1
Noot. Alle correlaties zijn significant bij een α van .01   Nlaag = 260, Nmidden = 932-933

In Tabel 6.12. zijn de intercorrelaties weergegeven voor personen met een hogere leeftijd (45 t/m 65).

Tabel 6.12. Intercorrelaties subtests ACT Algemene Intelligentie bij hoge leeftijd (45 tot 65) – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1
Figurenreeksen	.55	1
Verbale Analogieën	.50	.51	1
g-score	.80	.78	.87	1
Noot. Alle correlaties zijn significant bij een α van .01.   N = 640.

Ook in deze steekproef verschilden de correlaties niet significant van elkaar tussen de laagste en middelste leeftijdscategorieën. Tussen de middelste en de hoogste leeftijdscategorieën vonden we drie significante verschillen. De Cijferreeksen-Verbale Analogieën relatie liet het grootste verschil zien (Δr = .15, Z = 2.99, p = .00). Hoewel de correlaties Cijferreeksen-g-score (Z = 2.28, p = .02) en Verbale Analogieën-g-score (Z = 3.23, p = .00) significant van elkaar verschilden, waren deze verschillen in absolute zin zeer klein (beiden Δr = .05).

Ook in deze steekproef bevonden zich de meeste verschillen tussen de middelste en hoogste leeftijdscategorie. De correlaties Cijferreeksen-Verbale Analogieën (Z = 3.19, p = .00) en Figurenreeksen-Verbale Analogieën (Z = 2.86, p = .00) lieten de grootste verschillen zien, hoewel deze verschillen in absolute zin niet erg groot waren (respectievelijk Δr = .11 en Δr = .10). Hetzelfde gold voor de relatie tussen Cijferreeksen en de g-score (Δr = .05, Z = 2.78, p = .01) en Verbale Analogieën en de g-score (Δr = .03, Z = 3.03, p = .00).

Een principale component analyse toonde aan dat er één component was die de relaties tussen de subtests verklaarde, respectievelijk verklaarde deze 74.5%, 73.9% en 67.8% van de variantie bij personen uit de laagste, middelste en hoogste leeftijdscategorie. De ladingen op deze component waren nagenoeg gelijk aan elkaar (.86 bij laag/midden, .82 bij hoog).

Conclusies leeftijd

 Hoewel klein in absolute zin leken er wel verschillen in intercorrelaties te zijn op basis van leeftijd. Een mogelijke verklaring is het feit de ACT Algemene Intelligentie een test is die met de computer afgenomen wordt, waarbij het bekend is dat ouderen hier meer moeite mee kunnen hebben (McDonald, 2002; Steinmetz, Brunner, Loarer, & Houssemand, 2002). Ouderen kunnen überhaupt anders tegenover tests staan dan jongeren (Birkhill & Schaie, 1975). Echter, dit verklaart niet direct waarom de meeste verschillen tussen de middelbare en hoogste leeftijdsgroep gevonden werden. Gezien de effectgrootten kunnen we al met al concluderen dat de structuur van de ACT Algemene Intelligentie hetzelfde is voor verschillende leeftijdsgroepen.

6.3.4.4. Intercorrelaties naar opleidingsniveau

 Totale steekproef

In Tabel 6.13. staan onder de diagonaal de intercorrelaties weergegeven voor personen met een laag opleidingsniveau en boven de diagonaal voor mensen met een gemiddeld opleidingsniveau. Meer informatie over de indeling in deze categorieën is te vinden in Tabel 6.33. en 6.34.

Tabel 6.13. Intercorrelaties subtests ACT Algemene Intelligentie bij laag en middelbaar opleidingsniveau – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.45g	.46h	.82j
Figurenreeksen	.59a	1	.50i	.72k
Verbale Analogieën	.44b	.47c	1	.88l
g-score	.87d	.80e	.86f	1
Noot. Alle correlaties zijn significant bij een α van .01.   a N = 767, b N = 464, c N = 463, d N = 1027, e N = 1026, f N = 723, g N = 1588, h N = 1715, i N = 1723, j N = 2209, k N = 2217, l N = 2344.

In Tabel 6.14. zijn de intercorrelaties weergegeven voor mensen met een hoog opleidingsniveau. Meer informatie over de indeling van verschillende opleidingsniveaus in deze categorie is te vinden in Tabel 6.33. en 6.34.

Tabel 6.14. Intercorrelaties subtests ACT Algemene Intelligentie bij hoog opleidingsniveau – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1
Figurenreeksen	.49a	1
Verbale Analogieën	.46b	.47d	1
g-score	.80d	.75e	.88f	1
Noot. Alle correlaties zijn significant bij een α van .01   a N = 1178, b N = 1178, c N = 1027, d N = 1479, e N = 1328, f N = 1328.

 Voor zowel de vergelijking tussen laag-midden, laag-hoog en midden-hoog gold dat de correlatie tussen Cijferreeksen en Figurenreeksen, Cijferreeksen en de g-score en Figurenreeksen en de g-score significant van elkaar verschilden. De verschillen bij de eerstgenoemde correlatie waren het grootste (Δr = .14 bij laag-midden, Δr = .10 bij laag-hoog en midden-hoog). De verschillen bij de andere twee correlaties waren kleiner (tussen de Δr = .05 en Δr = .07).

De eerste component verklaarde respectievelijk 62.5%, 67.0% en 64.6% van de totale variantie in de scores op de subtests voor laag-, middelbaar- en hoger opgeleiden. De ladingen op deze component waren vergelijkbaar qua hoogte (respectievelijk gemiddeld .79, .82 en .80).

 Kandidaatssteekproef

Tabel 6.15. Intercorrelaties subtests ACT Algemene Intelligentie bij VMBO en MBO – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.53	.49	.80
Figurenreeksen	.52	1	.49	.76
Verbale Analogieën	.35	.44	1	.87
g-score	.73	.75	.84	1
Noot. Alle correlaties zijn significant bij een α van .01.   NVMBO = 204, NMBO = 1094-1095.

 

Tabel 6.16. Intercorrelaties subtests ACT Algemene Intelligentie bij HBO en WO – totale steekproef.
	Cijferreeksen	Figurenreeksen	Verbale   Analogieën	g-score
Cijferreeksen	1	.38	.38	.79
Figurenreeksen	.45	1	.38	.72
Verbale Analogieën	.34	.38	1	.76
g-score	.77	.73	.78	1
Noot. Alle correlaties zijn significant bij een α van .01.   NHBO = 402, NWO = 326-327.

Gezien het grote aantal geteste verschillen in correlaties volstaan we hier met een samenvatting. Gemiddeld over de 36 geteste correlaties waren de absolute verschillen klein (.06). Van deze 36 geteste relaties waren er 9 significant. Vier van deze significante verschillen in correlaties waren die tussen één van de subtests en de g-score, de overige dus bij correlaties tussen subtests onderling. Er bevonden zich geen verschillen in correlaties tussen de VMBO- en HBO-groep (zie Tabel 6.15.), en ook niet tussen de HBO- en WO groep (zie Tabel 6.16.). Tussen de MBO- en WO groep werden de meeste significante verschillen gevonden (vier) – waarbij deze verschillen ook wat groter waren (Δr = .10-.15). Het vaakst werd een significant verschil gevonden in de relatie tussen Cijferreeksen en Verbale Analogieën, en deze verschillen waren ook relatief het grootst (Δr = .15 voor VMBO-MBO, Δr = .16 voor MBO-HBO en Δr = .11 voor MBO-WO).

De eerste component verklaarde respectievelijk 62.5%, 67.0%, 59.4% en 58.8% van de totale variantie in de scores op de subtests voor de VMBO-, MBO-, HBO- en WO-groep. De ladingen op deze component waren vergelijkbaar qua hoogte (respectievelijk gemiddeld .79, .82, .77 en .77).

Gezien het feit dat er tussen de opleidingsniveaus wat meer verschillen in correlaties waren, en de normgroepen gebaseerd zijn op deze opleidingsniveaus, achtten wij het noodzakelijk de equivalentie van de factorstructuur uitgebreider te onderzoeken. Dat wil zeggen, een score behaald door iemand met een MBO-opleiding moet dezelfde betekenis hebben als de score behaald door een persoon met een WO-opleiding.

Om dit te onderzoeken is de meetinvariantie van het structurele model zoals weergegeven in Figuur 6.1 tussen de vier groepen getoetst. In deze analyse is een model waarin de drie factorladingen van Cijferreeksen, Figurenreeksen en Verbale Analogieën op g tussen de vier groepen gelijkgesteld zijn vergeleken met een model waarin dit niet het geval was (en de factorladingen dus vrij geschat werden). De fit van het meer restrictieve model is vergeleken met het baseline model; bij een niet-significant verschil in χ²-waarden of wanneer het verschil in CFI- waarden tussen de modellen ≤ .01 is (Chen, 2007) kan men spreken van zwakke meetinvariantie. De analyses zijn uitgevoerd met het lavaan (Rosseel, 2012) en semTools (semTools Contributors, 2016) pakket in R (R Core Team, 2016).

Tabel 6.17. Fit-statistieken factormodellen.
	χ2 (df)	p	Δχ2 (Δdf)	CFI	ΔCFI
Baseline model	0 (0)	1	–	1	–
Gelijke ladingen	11.398 (6)	.08	11.398 (6)	.995	-.005

De fit-statistieken zoals weergegeven in Tabel 6.17. leveren bewijs voor zwakke meetinvariantie: het verschil in χ²-waarden is niet significant, en het verschil in CFI-waarden is kleiner dan .01 (namelijk .005). Dit houdt in dat de betekenissen van de scores op de Cijferreeksen, Figurenreeksen en Verbale Analogieën hetzelfde zijn bij de vier opleidingsniveaus, en we de scores op de algemene factor dus hetzelfde kunnen interpreteren.

6.3.5. Conclusies met betrekking tot intercorrelaties subtests

De bevindingen in dit onderzoek tonen aan dat de drie subtests van de ACT Algemene Intelligentie hoge en verwachte intercorrelaties laten zien. Dit levert tevens bewijs voor de g-factor en dus ook voor de theoretische onderbouwing van de ontwikkeling van de adaptieve capaciteitstests van Ixly. Ook wanneer de intercorrelaties afzonderlijk voor mannen/vrouwen, autochtonen/allochtonen, verschillende leeftijdsgroepen en opleidingsniveaus werden bekeken dan hielden deze conclusies stand. Hoewel er verschillen in de hoogten van de correlaties tussen groepen werden gevonden, kunnen we concluderen dat de scores op de ACT Algemene Intelligentie bij verschillende groepen dezelfde betekenis lijken te hebben. Dit biedt sterk bewijs voor de interne structuur van de ACT Algemene Intelligentie en hiermee voor de begripsvaliditeit.

6.4. Onderzoek naar de factorstructuur van de ACT Algemene Intelligentie: structurele modellen

 De intercorrelaties zoals hiervoor besproken ondersteunen al de aanwezigheid van een g-factor die de scores op alle drie de subtests beïnvloedt. Meer formeel kan dit in een structureel model getest worden. Dit model is weergegeven in Figuur 6.1.

Figuur 6.1. Structureel model van ACT Algemene Intelligentie.

Bovenstaande model is in AMOS 20 (Arbuckle, 2011) geschat, met de maximum likelihood schattingsmethode. De factorladingen van de drie subtests op de g-factor zijn nagenoeg identiek: dit betekent dat de scores op de subtests evenveel beïnvloed worden door een algemeen intellectueel denkniveau. De factorladingen zijn, conform de g-theorie, relatief hoog: ongeveer 60% van de variantie in de subtestscores wordt verklaard door g.

Het nadeel van het bovenstaande model is dat er niet gekeken kan worden naar hoe goed het gekozen model een beschrijving van de data is (‘model fit’), omdat er geen vrijheidsgraden over zijn. Beter zou het zijn om itemscores in plaats van subtestscores als geobserveerde variabelen te gebruiken. Echter, het probleem bij adaptieve tests is dat er veel missende waarden zijn op itemscores – niet iedereen krijgt dezelfde items te zien.

Om toch een idee te krijgen of de veronderstelde factorstructuur – een hogere orde g-factor die scores op de de subtests beïnvloedt – wordt teruggevonden bij de ACT Algemene Intelligentie is er een extra onderzoek uitgevoerd. In dit onderzoek zijn voor iedere subtests de vijf items opgezocht die de meeste responses hadden in de kandidaatssteekproef: de antwoorden op deze 15 items werden uit het volledige databestand gefilterd en in een nieuw databestand opgeslagen. Vervolgens zijn met Mplus 6 (Muthén & Muthén, 2010) op basis van deze dataset weer 10 datasets gecreëerd waarbij de missende waarden geïmputeerd werden. Zo ontstonden er dus 10 datasets (ieder N = 2334) met volledige antwoorden op alle 15 items (5 per subtest).

Allereerst is er op basis van exploratieve factoranalyse gekeken in hoeverre er een hiërarchische structuur naar voren kwam. In iedere dataset zijn daarom twee factoranalyses gedaan:[4]

1. Eén met promax rotatie waarbij drie factoren werden geëxtraheerd. Vervolgens werden de scores op deze factoren opgeslagen.
2. Op deze in Stap 1 verkregen scores werd weer een factoranalyse gedaan waarbij één factor geëxtraheerd werd.

Uit de eerste factoranalyses bleek dat de drie factoren redelijk goed naar voren kwamen, dat wil zeggen, item1-item5 (Cijferreeksen) laadden op Factor 1, item6-item10 (Figurenreeksen) laadden op Factor 2 en item11-item15 (Verbale Analogieën) laadden op Factor 3. Echter, er was ook vaak sprake van kruisladingen (bijvoorbeeld item1 laadt ook sterk op Factor 3, naast Factor 1); dit is ook te verwachten bij een sterk aanwezige g-factor.

De analyses in Stap 2 lieten zien dat de eerste factor gemiddeld 55% (uiteenlopend van 49% tot en met 59% over de tien datasets) van de variantie verklaarde in de onderliggende scores. De gemiddelde factorladingen op de eerste factor was .71, lopend van -.26 – .85. Er was, zoals duidelijke wordt uit de negatieve factorlading, één dataset (dataset 6) die afwijkende waarden liet zien. De gemiddelde factorlading zonder deze dataset was .74, uiteenlopend tussen de .48 en .85. Deze resultaten bieden verdere ondersteuning voor de g-factor in de ACT Algemene Intelligentie.

Ter bevestiging hiervan zijn ook structurele modellen getoetst, waarbij gekeken is naar de fit van de modellen. Er werden drie modellen getoetst (standaard modellen voor intelligentie uit de literatuur, zie Jensen, 1998 en Gignac, 2016), die zijn weergegeven in Figuur 6.2.

 Figuur 6.2. Structurele modellen van de ACT Algemene Intelligentie.

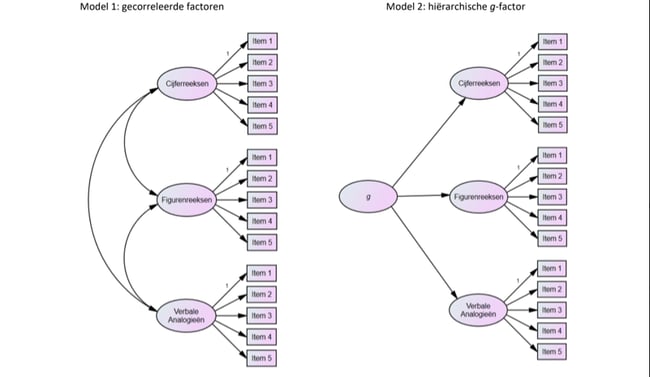
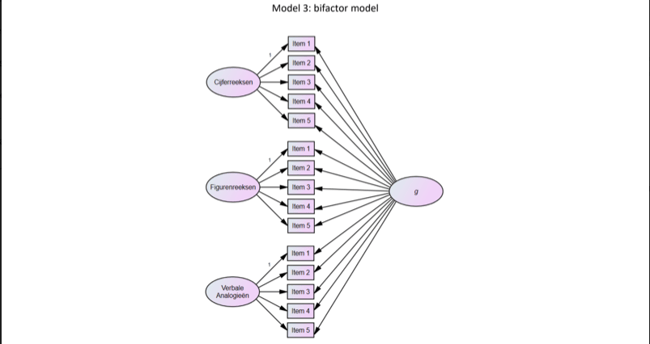
De fit-waarden zijn weergegeven in Tabel 6.18: Model 1 en 2 zijn equivalent aan elkaar en laten daarom ook dezelfde fit-waarden zien. Dit zijn de gemiddelde waarden over de 10 datasets.[5]

Tabel 6.18. Fit-waarden van structurele modellen zoals weergegeven in Figuur 6.2.
	χ2 (df)	p	CFI	TLI	RMSEA
Model 1 + Model 2	1042.30 (87)	< .001	.856	0.826	0.068
Model 3	768.471 (75)	< .001	.894	0.851	0.063
Noot. Waarden zijn gemiddelden over 10 geïmputeerde datasets.

Volgens de richtlijnen van Hu en Bentler (1999) zoals beschreven in Dimitrov (2012) duiden de fit-waarden van Model 1 en Model 2 op redelijke fit[6]: de CFI-waarde is aan de lage kant, maar de RMSEA-waarde is wel indicatief voor goede fit. Het gekozen model lijkt dus een adequate beschrijving van de data te geven, hoewel er nog wel ruimte voor verbetering mogelijk is. De fit van Model 3 is beter.[7] Hier moet echter bij opgemerkt worden dat het schatten van dit model problematisch was in de zin dat er vaak onrealistische waarden gevonden werden (bijv. factorladingen > 1, zogenaamde ‘Heywood-case’). Deze fit-waarden dienen dus met voorzichtigheid geïnterpreteerd te worden.

Een belangrijke bevinding in Model 1 was dat de correlaties tussen de latente factoren voor Cijferreeksen, Figurenreeksen en Verbale Analogieën hoog waren, gemiddeld over de 10 datasets namelijk .74, .81 en .71 (gemiddeld .78). Deze correlaties zijn zo hoog dat de factoren moeilijk van elkaar te onderscheiden zijn: dit duidt dus op een aanwezige g-factor. Een tweede belangrijke bevinding was dat in Model 2 de factorladingen van de latente Cijferreeksen, Figurenreeksen en Verbale Analogieën-dimensies op de g-factor zeer hoog waren, namelijk .88, .85 en .92 (gemiddelden over de 10 datasets). Dit betekent dat een groot deel van de variantie in de scores op de subtests verklaard kon worden door de algemene factor. Dus hoewel de fit van de modellen voldoende maar niet zeer goed was, duidden de gevonden relaties wel op een sterk aanwezige g-factor.

Conclusies

 Het hiervoor beschreven onderzoek bevestigt de veronderstelde factorstructuur van de ACT Algemene Intelligentie, waarbij een overkoepelende algemene intelligentiefactor de scores op de onderliggende subtests beïnvloedt. Hierbij moet wel opgemerkt worden dat dit gezien moet worden als een indicatie: dit onderzoek is gebaseerd op slechts vijf items van iedere subtest, waarbij een groot deel (gemiddeld 50%) van de waarden – die per definitie ontstaan bij een adaptieve test – ontbraken en dus geïmputeerd zijn. Echter, gecombineerd met de bevindingen gebaseerd op alle andere onderzoeken in dit hoofdstuk kunnen we concluderen dat de factorstructuur van de ACT Algemene Intelligentie goed onderbouwd is.

6.5. Externe validiteit: Soortgenotenvaliditeit

Voor het onderzoeken naar de externe validiteit zijn twee onderzoeken uitgevoerd met soortgenoten, oftewel tests die hetzelfde construct – of sterk gerelateerde constructen – als de ACT Algemene Intelligentie zouden moeten meten. Bij het validiteitsonderzoek is parallel aan de ACT Algemene Intelligentie telkens een andere vergelijkbare vragenlijst opgenomen, namelijk de Multiculturele Capaciteiten Test – Hoger niveau (MCT-H, Bleichrodt & Van den Berg, 2006) en een begrijpend lezen-test (ontwikkeld door Ixly). Beide onderzoeken worden hieronder besproken.

6.5.1. Onderzoek met de MCT-H

6.5.1.1. Introductie

In dit onderzoek zijn de relaties onderzocht tussen scores op de ACT Algemene Intelligentie en de MCT-H ter ondersteuning van de convergente en discriminante validiteit. De MCT-H is een intelligentietest die, de naam zegt het al, met name ontwikkeld is om de partijdigheid bij intelligentietests – dat wil zeggen dat allochtonen vaak lager scoren dan autochtonen – te reduceren. De gehele test bestaat uit acht subtests die vier factoren meten: logisch redeneren & ruimtelijk inzicht, numerieke vaardigheden, verbale vaardigheden en perceptuele snelheid (Bleichrodt & Van den Berg, 2006). De betrouwbaarheid en validiteit van deze test zijn goed, wat blijkt uit een positieve beoordeling door de Cotan in 2006. Voor het gestelde doel in dit onderzoek – het aantonen van convergente validiteit – en om de testtijd voor kandidaten te beperken zijn uit de testbatterij vier subtests gekozen die qua itemformat, logica en domein (numeriek, figuratief en verbaal) het meest lijken op de subtests van de ACT Algemene Intelligentie. Dit waren Cijferreeksen, Componenten, Exclusie en Woordanalogieën.

6.5.1.2. Onderzoeksopzet

Op 1, 2 en 3 augustus 2016 is er een onderzoek op locatie bij Ixly in Utrecht uitgevoerd. Gedurende de dag waren er vijf sessies van 2 uur waarin respondenten verschillende tests afnamen in een testzaal, waaronder de ACT Algemene Intelligentie en de MCT-H. In de testzaal bevonden zich 9 laptops met internetverbinding waar de tests op gemaakt dienden te worden: in iedere sessie bevonden zich 7 tot 9 personen. De respondenten werden door een medewerker van Ixly ontvangen in de hal van het testzalencomplex. Toen alle respondenten gearriveerd waren, werden zij naar de testzaal gebracht, waarna de testleider een uitgebreide instructie gaf over het doel van het onderzoek en het verloop van het onderzoek. Ook werden de respondenten ingelicht over het feit dat alle data anoniem verwerkt zou worden en kregen zij te horen dat zij op ieder moment mochten stoppen met het onderzoek. Na de instructies hebben allen een toestemmingsverklaring ondertekend. Na afloop van het onderzoek kregen de respondenten een debriefing waarin zij bedankt werden voor het onderzoek.

Omdat de ACT Algemene Intelligentie en MCT-H tests identieke vraagtypen bevatten (cijferreeksen en verbale analogieën) is, om leereffecten te voorkómen, de volgorde van de twee testbatterijen gerandomiseerd. De ene groep maakte eerst de ACT Algemene Intelligentie en daarna de MCT-H, terwijl de andere groep eerst de MCT-H voltooide en daarna de ACT Algemene Intelligentie. Omdat er op verschillende dagdelen getest werd en dit van invloed kan zijn op de testresultaten (bijvoorbeeld omdat mensen moe zijn na een dag hard werken en hierdoor minder geconcentreerd kunnen werken in de avond), zijn de groepen met verschillende testvolgordes gelijk verdeeld over de dagdelen. Zo was er uiteindelijk sprake van een gebalanceerd onderzoeksdesign (zie Tabel 6.19.).

Tabel 6.19. Onderzoeksopzet.
		Dagdeel	1e test	2e test
Dag 1	Groep 1	1	ACT	MCT-H
	Groep 2	2	MCT-H	ACT
	Groep 3	3	ACT	MCT-H
	Groep 4	4	MCT-H	ACT
	Groep 5	5	ACT	MCT-H
Dag 2	Groep 6	1	MCT-H	ACT
	Groep 7	2	ACT	MCT-H
	Groep 8	3	MCT-H	ACT
	Groep 9	4	ACT	MCT-H
	Groep 10	5	MCT-H	ACT

6.5.1.3. Hypothesen

 Convergente validiteit

Gezien het itemtype van de verschillende subtests van de ACT en de MCT-H kunnen we hypothesen opstellen over de sterkte van de onderlinge relaties tussen deze subtests. Zo kunnen we bijvoorbeeld verwachten dat de relatie tussen de Cijferreeksentest van de ACT Algemene Intelligentie het sterkst is met de Cijferreeksentest van de MCT-H. Specifieker, dat de correlatie van de Cijferreeksen (ACT Algemene Intelligentie) met de Cijferreeksen (MCT-H) sterker is dan de correlatie van de Cijferreeksen (ACT Algemene Intelligentie) met de andere subtests. Hetzelfde geldt voor Verbale Analogieën van de ACT Algemene Intelligentie en Woordanalogieën van de MCT-H. Hoewel minder één-op-één, kunnen we dit ook verwachten voor de relaties tussen Figurenreeksen (ACT Algemene Intelligentie) en Componenten en Exclusie (MCT-H): alle drie de tests zijn figuratieve tests, en doen een beroep op het abstracte denkvermogen.

Uiteindelijk bestond de volledige steekproef uit 92 personen; 1 persoon was niet naar de testzaal gekomen maar had de tests thuis gemaakt, een ander persoon was wel naar de onderzoekslocatie gekomen maar gaf aan door slecht zicht niet deel te kunnen nemen. Deze persoon heeft vervolgens wel de tests thuis gemaakt. Echter, omdat deze 2 respondenten de tests in een geheel andere setting hebben afgerond, zijn zij uit de steekproef verwijderd. De steekproef bestond uit 42 mannen (46%) en 50 vrouwen (54%), met een gemiddelde leeftijd van 42.5 jaar (SD = 13.9) variërend van 18 tot en met 65 jaar. Vergeleken met CBS gegevens van 2013 (het laatste jaar waarvoor volledige gegevens beschikbaar zijn) was deze steekproef representatief voor de Nederlandse beroepsbevolking wat betreft geslacht (χ² = 3.25, df = 1, p = .07) en redelijk representatief wat betreft leeftijd[8] (χ² = 9.50, df = 3, p = .00, Cramer’s V = .18). Er bevonden zich 6 personen in de steekproef die als allochtoon gekwalificeerd konden worden (6.5%). Hiermee waren allochtonen ondervertegenwoordigd in de huidige steekproef ten opzichte van de beroepsbevolking. De verdeling van de proefpersonen qua opleidingsniveau is weergegeven in Tabel 6.20.

Tabel 6.20. Verdeling steekpoef over opleidingsniveaus.
	Aantal	%
Lagere school/basisonderwijs	1	1
VMBO: basisberoepsgerichte leerweg (BB)	6	7
VMBO: Gemengde leerweg (GL)	2	2
VMBO: Theoretische leerweg (TL)	4	4
MBO 1: Assistent beroepsbeoefenaar	1	1
MBO 2: Medewerker	1	1
MBO 3: Zelfstandig medewerker	7	8
MBO 4: Middenkaderfunctionaris	17	18
HAVO	9	10
VWO	2	2
HBO: Oude stijl	14	15
HBO: Bachelor	10	11
HBO: Master	3	3
WO: Bachelor	3	3
WO: Master	9	10
WO: Doctorandus	3	3
Totaal	92	100

Het CBS hanteert verschillende indelingen, één met vijf categorieën en drie categorieën. Om onze opleidingsverdeling vergelijken met die van het CBS zijn onze opleidingsgroepen opnieuw gecodeerd in de vijf en drie categorieën van het CBS. Vergeleken met beide indelingen leek de steekproef redelijk representatief wat betreft opleidingsniveau (5 categorieën: χ² = 6.15, df = 4, p = .19; 3 categorieën χ² = 7.15, df = 2, p = .02, V = .20).

De meeste mensen waren werkzaam in de sectoren Gezondheids- en welzijnszorg (22%), Overige dienstverlening (22%) en Onderwijs (14%), de overige respondenten waren redelijk verdeeld over de verschillende werksectoren (zie Tabel 6.21.).

Tabel 6.21. Verdeling steekproef over werksectoren.
	Aantal	%
Landbouw, bosbouw en visserij	2	2
Industrie	2	2
Bouwnijverheid	3	3
Handel	5	5
Vervoer en opslag	1	1
Horeca	8	9
Informatie en communicatie	5	5
Financiële dienstverlening	3	3
Specialistische zakelijke diensten	1	1
Verhuur en overige zakelijke diensten	2	2
Openbaar bestuur en overheidsdiensten	4	4
Onderwijs	13	14
Gezondheids- en welzijnszorg	20	22
Cultuur, sport en recreatie	3	3
Overige dienstverlening	20	22
Totaal	92	100

De meerderheid van de proefpersonen was werkzaam (85%), de overige personen bestonden uit studenten/scholieren (9%) en werkzoekenden (6%). Deze verdeling – studenten uitgesloten – kwam exact overeen met de verdeling in de beroepsbevolking (χ² = .00, df = 1, p = .95). De volledige verdeling naar werksituatie is weergegeven in Tabel 6.22.

Tabel 6.22. Verdeling steekproef over werksituatie.
	Aantal	%
Loondienst tijdelijk contract (incl. uitzendcontract)	14	15
Loondienst vast contract	52	57
Student of scholier	8	9
Werkzoekende zonder uitkering	2	2
Werkzoekende met uitkering	4	4
Eigen onderneming met personeel	2	2
Zelfstandige zonder personeel (ZZP)	10	11
Totaal	92	100

6.5.1.4. Resultaten

Betrouwbaarheid

 In Tabel 6.23. zijn de betrouwbaarheden weergegeven van de verschillende tests. De betrouwbaarheden van de subtests van de ACT Algemene Intelligentie zijn de empirische betrouwbaarheden (Du Toit, 2003; zie Hoofdstuk 5). De betrouwbaarheden van de subtests van de MCT-H zijn de betrouwbaarheden zoals vermeld in de handleiding van de MCT-H[9] (Bleichrodt & Van den Berg, 2006).

De g-score van de ACT is een gewogen gemiddelde op basis van de drie θ-scores van de subtests: de weging vindt plaats op basis van de betrouwbaarheid van de subtestscores (zie Hoofdstuk 3, sectie 3.6.). De g-score van de MCT-H is simpelweg de somscore van de vier subtests. Voor de betrouwbaarheden van beide g-scores zijn Cronbach’s alpha waarden berekend, aan de hand van de betreffende subtests in de huidige steekproef.

Tabel 6.23. Betrouwbaarheden van ACT Algemene Intelligentie en MCT-H.
	α
ACT:
Cijferreeksen	.79
Figurenreeksen	.80
Verbale Analogieën	.89
g-score	.83
MCT-H:
Cijferreeksen	.80
Componenten	.84
Exclusie	.74
Woordanalogieën	.86
g-score	.86

Testvolgorde

Allereerst hebben we gekeken naar het effect van de volgorde van het maken van de tests. Er werd alleen een significant effect gevonden bij de Woordanalogieëntest van de MCT-H (F(1,90)= 4.32, p = .04). Echter, dit effect was in tegengestelde richting van wat te verwachten viel: personen die de MCT-H test eerst hadden gedaan scoorden hoger (en niet lager) op de Woordanalogieëntest van de MCT-H dan mensen die eerst de ACT hadden gedaan. Bij een leereffect zou dit juist precies andersom moeten zijn. Lettend op de effectgrootten (Cohen’s d) in plaats van p-waarden waren de gevonden verschillen relatief klein (gemiddeld .21). Controleren voor deze effecten door middel van een dummy-variabele (“ACT eerst” of “MCT-H eerst”) had dan ook geen effect op de resultaten. Om het overzichtelijk te houden hebben we daarom de resultaten van de analyses zonder deze controle weergegeven.

Convergente en discriminante validiteit

In Tabel 6.24. zijn de correlaties weergegeven tussen de verschillende subtests van de ACT en de MCT-H en hun respectievelijke g-scores. Ook zijn de correlaties na attenuatiecorrectie weergegeven. Attenuatie is het verschijnsel dat de correlatie tussen twee variabelen afneemt naarmate de betrouwbaarheid van de variabelen lager is. Dit betekent dat er een schatting wordt gegeven van de correlatie in het hypothetische geval dat er geen attenuatie (dus wanneer de constructen zonder onbetrouwbaarheid gemeten zouden zijn) optreedt.

In overeenkomst met de verwachting zijn de correlaties over het algemeen hoog. De correlaties tussen de g-scores (r = .80) en van de subtests zijn zelfs van een grootte die verwacht wordt bij een hertest van hetzelfde instrument. Wanneer we naar de correlaties na correctie voor onbetrouwbaarheid kijken, kunnen we concluderen dat de tests vrijwel hetzelfde meten (g-score: r = .95, cijferreeksen: r = .91).

Wat betreft convergente en discriminante validiteit zijn de resultaten grotendeels in lijn met onze verwachtingen. De gemiddelde hetero trait mono method correlatie (i.e., correlaties tussen de ACT Algemene Intelligentie subtests onderling) was .62, voor zowel de ACT Algemene Intelligentie als de MCT-H. De gemiddelde mono trait hetero method correlatie (i.e., correlatie tussen de twee cijferreeksentests) was .67 (.81 na attenuatiecorrectie). De gemiddelde hetero trait hetero method (i.e. correlatie tussen Cijferreeksen (ACT Algemene Intelligentie) en Woordanalogieën van de MCT-H) was .59 (.72 na attenuatiecorrectie). Een formele statistische toets wees uit dat deze gemiddelde correlaties niet significant van elkaar verschilden in hoogte; echter, dit is ook wel te verwachten, aangezien de g-factor sterk in de scores op alle subtests aanwezig is en dus de onderlinge relaties tussen deze subtests beïnvloedt (zie volgende sectie).

Structurele modellen

In het voorgaande hebben we gekeken naar de relaties tussen de g-scores als somscores van de subtests. Deze resultaten gaven al aan dat de g-scores van beide tests sterk met elkaar samenhingen. Echter, intelligentie – of g – kan het best geconceptualiseerd worden als een latente trek met verschillende indicatoren (scores op de subtests in ons geval).

Daarom hebben we de correlatiematrix (zoals weergegeven in Tabel 6.24.) gebruikt als input voor een aantal structurele modellen, om de overeenkomst tussen de g-scores gebaseerd op de twee verschillende tests te kunnen bepalen.

Er zijn twee modellen getoetst. Het eerste model was een hiërarchisch model waarbij de subtests van dezelfde soort indicatoren vormden van drie latente trekken (Numeriek, Abstract en Verbaal), die weer indicatoren vormden van de g-score (Figuur 6.3.).

 Figuur 6.3. Structureel model met één g-score voor ACT Algemene Intelligentie en MCT-H.

Noot. Voor de leesbaarheid zijn de residuen niet weergegeven. Residu van de latente trek Verbaal is gefixeerd op 0. Alle ladingen zijn significant bij een α van .001.

In het model zoals weergegeven in Figuur 6.3. was de residu voor de latente trek Verbaal een zeer klein, niet significant negatief getal: dit duidt erop dat alle variantie in de Verbale factor door de g-score verklaard wordt. Omdat de variantie van het residu niet significant was, mag deze op 0 gezet worden (Muthén, 2008). De fit van dit model was uitstekend, (χ²(12) = 12.86, p = .38, CFI = .998, RMSEA = .028, SRMR = .029). De factorladingen van de indicatoren op de trekken Numeriek, Abstract en Verbaal zijn hoog. De ladingen van deze drie trekken op de g-score zijn vrijwel gelijk aan 1: dit betekent dat de algemene intelligentie van een persoon vrijwel geheel verantwoordelijk is voor het numerieke, abstracte en verbale denkvermogen van deze persoon.

Ook hebben we getoetst of de ladingen van de twee tests op hun hogere orde factor even sterk waren. De methode was als volgt: we stelden het pad van “Numeriek” naar “ACT: Cijferreeksen” gelijk aan het pad van “Numeriek” naar “MCT-H: Cijferreeksen”. Vervolgens keken we naar het verschil in fit met het bovenstaande model (op basis van het verschil in χ²-waarden). Als het model aanzienlijk ‘slechter’ wordt, dan kunnen we concluderen dat de ladingen niet hetzelfde zijn. Echter, voor elk van de ladingen gold dat het model nauwelijks veranderde wat betreft fit, waaruit we kunnen concluderen dat de ACT Algemene Intelligentie en MCT-H even sterke indicatoren voor de factoren waren.

De relaties kunnen ook anders gemodelleerd worden: het tweede model bestond uit twee g-scores, voor iedere test één, die vervolgens gecorreleerd werden (Figuur 6.4.). De fit van dit model was ook zeer goed, maar iets minder goed dan Model 1 (χ²(13) = 18.38, p = .14, CFI = .986, RMSEA = .067, SRMR = .035). Een formele Δχ²-toets wees ook uit dat Model 1 een betere beschrijving van de data was (Δχ² = 5.51, df = 1, p = .02). De twee latente g-scores gebaseerd op de twee verschillende testbatterijen zijn identiek (r = .99). Ook hieruit kunnen we concluderen dat de ACT Algemene Intelligentie het beoogde construct, intelligentie, blijkt te meten.

Net als in het eerste model zijn de factorladingen tussen de tests vergeleken (bijv. het pad van “g-score: ACT” à “ACT: Verbale Analogieën” (.75) en het pad “g-score: MCT-H” à “MCT-H: Woordanalogieën” (.80)). Opnieuw bleek dat deze niet significant van elkaar verschilden. Hieruit kunnen we concluderen dat de factorstructuren – met een g-factor – van beide tests hetzelfde zijn).

Figuur 6.4. Structureel model met twee g-scores gebaseerd op de ACT Algemene Intelligentie en MCT-H.

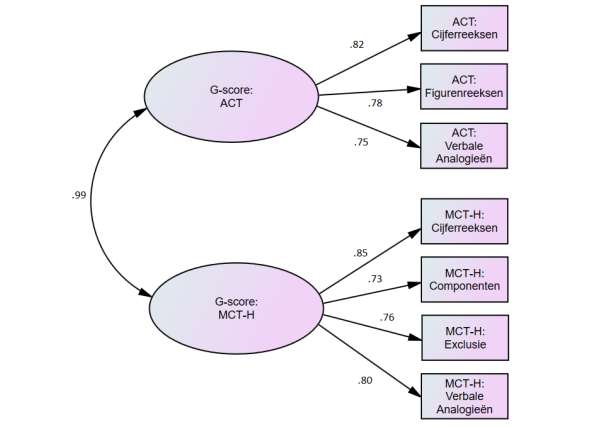
Noot. Alle ladingen zijn significant bij een α van .001.

Tabel 6.24. Correlaties tussen de verschillende subtests van de ACT en de MCT-H en hun respectievelijke g-scores.

	ACT:	ACT:	ACT:	ACT:	MCT-H:	MCT-H:	MCT-H:	MCT-H:
	g-score	Cijferreeksen	Figurenreeksen	Verbale Analogieën	g-score	Cijferreeksen	Componenten	Exclusie
ACT: g-score	1
ACT: Cijferreeksen	.84	1
ACT: Figurenreeksen	.83	.63	1
ACT: Verbale Analogieën	.90	.60	.63	1
MCT-H: g-score	.80/.95	.75/.91	.72/.87	.66/.75	1
MCT-H: Cijferreeksen	.77/.95	.72/.91	.62/.78	.67/.79	.85	1
MCT-H: Componenten	.59/.71	.58/.71	.62/.76	.44/.51	.83	.58	1
MCT-H: Exclusie	.65/.83	.63/.82	.59/.77	.53/.65	.82	.60	.64	1
MCT-H: Woordanalogieën	.70/.83	.62/.75	.59/.71	.60/.69	.88	.69	.60	.60
Noot. Alle correlaties zijn significant bij een α van .001. Met arcering zijn de convergente en divergente correlaties weergegeven, namelijk binnen een test en tussen tests, respectievelijk. De donkerste kleur duidt aan dat het hier om metingen van hetzelfde soort test gaat.

6.5.1.5. Conclusie

 De onderlinge relaties tussen scores op de subtests van de ACT en de MCT-H waren hoog, waarbij over het algemeen de relaties sterker waren voor subtests van hetzelfde soort. De correlaties tussen de beide g-scores en structurele modellen toonden aan dat de g-scores nauwelijks van elkaar te onderscheiden waren. Over het algemeen kunnen we op basis van deze resultaten dus concluderen dat de ACT: Algemene Intelligentie, die hetzelfde beoogt te meten als de MCT-H, namelijk intelligentie, dit ook daadwerkelijk doet. Dit draagt bij aan de begripsvaliditeit van de ACT Algemene Intelligentie.

6.5.2. Onderzoek naar de relatie tussen intelligentie en begrijpend lezen

6.5.2.1. Introductie

 Lezen, en met name begrijpend lezen, is een taak waarbij een beroep wordt gedaan op de cognitieve vermogens van een persoon. Er zijn volgens Aarnoutse en Van Leeuwe (1988) ten minste drie belangrijke redenen waarom intelligentietests en tests voor begrijpend lezen samenhangen; 1) beide soorten tests doen een beroep op de bekwaamheid in probleemsituaties de juiste verbanden te leggen, 2) in intelligentietests kunnen veel opdrachten slechts door middel van begrijpend lezen uitgevoerd worden en 3) het verbale gedeelte van veel intelligentietests vereist meer specifieke capaciteiten zoals leesvaardigheid of een bepaalde woordenschat.

Ook andere theoretische verklaringen kunnen aangedragen worden. Zo ging De Glopper (1996) na in hoeverre de vaardigheid in begrijpend lezen van leerlingen verklaard kan worden vanuit het vermogen tot zelfcontrole bij het leesproces in de vorm van planning, monitoring en evaluatie. Er kwam naar voren dat zelfcontrole erg belangrijk is voor begrijpend lezen en dat dit voor een belangrijk deel een gevolg was van een meer algemene intellectuele ontwikkeling.

Een andere verklaring wordt gezocht in het zogenaamde werkgeheugen – het opslaan en verwerken van informatie – wat vereist is bij de cognitieve processen die een rol spelen bij begrijpend lezen: zo dienen alinea’s aan elkaar verbonden te worden, informatie opgeslagen te worden voor later gebruik, er dienen verbanden gelegd te worden etc. (Cain, Oakhill, & Bryant, 2004; Daneman & Carpenter, 1980; de Jonge & de Jong, 1996). Dit werkgeheugen is op zijn beurt weer sterk gerelateerd aan algemene intelligentie – er is zelfs twijfel of deze twee constructen niet identiek aan elkaar zijn (Ackerman, Beier, & Boyle, 2005; Oberauer, Schulze, Wilhelm, & Süß, 2005).

Onderzoek heeft dan ook aangetoond dat scores op intelligentietests een relatief sterke samenhang vertonen met scores op tests voor begrijpend lezen. Correlaties variëren ongeveer tussen de .30 en .50 (waarbij sterkere relaties gevonden worden voor verbale capaciteiten; Aarnoutse en Van Leeuwe, 1988). Het meeste onderzoek naar intelligentie en begrijpend lezen is gedaan onder leerlingen in het basisonderwijs. Er lijkt echter bewijs te zijn dat de rol van intelligentie bij begrijpend lezen – vergeleken met bijvoorbeeld woordenschat of ‘technisch lezen’ (Aarnoutse en Van Leeuwe, 1988) – sterker wordt met leeftijd (Birch & Belmont, 1965; Singer, 1977).

Aangezien wij uitspraken willen doen over begrijpend lezen bij volwassen, kunnen we gebaseerd op de voorgaande discussie verwachten dat we een sterke relatie (r > .50, naar de maatstaven van Cohen, 1988) vinden tussen scores op de ACT Algemene Intelligentie en een test die de vaardigheid tot begrijpend lezen meet, waarbij we een sterker effect verwachten voor Verbale Analogieën dan voor Cijferreeksen en Figurenreeksen.

 6.5.2.2. Steekproef en procedure

 Om de bovenstaande hypothesen te toetsen is de data van kandidaten die de ACT Algemene Intelligentie en de begrijpend lezen-test hebben gemaakt uit de database van Ixly gehaald. Deze data is verzameld tussen december 2015 en 1 juli 2016. De kandidaten maakten deze tests als onderdeel van een selectieprocedure voor een gecombineerde baan en opleiding in de vervoersbranche.

De steekproef bestond uit in totaal 937 personen. Deze steekproef bestond voornamelijk uit mannen (91.5%). De gemiddelde leeftijd was 37 (SD = 11.2), uiteenlopend tussen de 18 en 61 jaar. De verdeling over de verschillende opleidingsniveaus is weergegeven in Tabel 6.25. Het overgrote deel bestond uit personen met een MBO achtergrond; dit is te verklaren door het niveau en het type werk waarvoor de kandidaten kwamen solliciteren.

Hoewel mannen duidelijk oververtegenwoordigd zijn in de steekproef hebben we genoeg vrouwen in de steekproef om voor geslacht te kunnen controleren bij de analyses. We kunnen verwachten dat opleidingsniveau een sterke relatie laat zien met zowel intelligentie (zie sectie 6.8.1.) en begrijpend lezen (Overmaat, Roed, & Ledoux, 2002): omdat verdeling wat betreft opleidingsniveau scheef was (de meeste kandidaten hadden een MBO opleiding, zie Tabel 6.25.) hebben we ook gecontroleerd voor opleidingsniveau in de analyses. Hiermee hebben we getracht de invloed van de kenmerken van de steekproef op de resultaten zo veel mogelijk te minimaliseren.

Tabel 6.25. Verdeling steekproef over opleidingsniveaus.
	Aantal	%
Lagere school/basisonderwijs	23	2.5
VMBO	135	14.4
MBO	680	72.6
HAVO	30	3.2
VWO	9	1.0
HBO	34	3.6
WO	6	0.6
Onbekend	3	0.3
Anders	17	1.8
Totaal	937	100

De testafname vond plaats tijdens een testdag voor toelating tot een werk- en opleidingstraject voor chauffeurs. Tijdens deze dag maken de deelnemers meerdere online tests en vragenlijsten. Deze tests worden in een vaste volgorde aangeboden. Deelnemers worden geïnstrueerd de tests op volgorde te maken. De tests zijn (op volgorde) de Werkgerelateerde Persoonlijkheidsvragenlijst (WPV), de ACT Algemene Intelligentie, de reactietijd- en concentratietest (de simpele reactietijdentest), de selectieve keuze reactietijdentest (de choice reactietijdentest) en ten slotte de Nederlandse taaltest S (een begrijpend lezen test). Voor dit onderzoek wordt alleen gebruik gemaakt van de resultaten van de ACT Algemene Intelligentie en de begrijpend lezen-test.

6.5.2.3. Instrumenten

 Intelligentie

De betrouwbaarheid van de g-score was .77 wanneer gebaseerd op Cronbach’s α-waarde, en .90 wanneer berekend aan de hand van de empirische betrouwbaarheid-methode. De waarden voor de empirische betrouwbaarheden waren respectievelijk .73, .72 en .86 voor Cijferreeksen, Figurenreeksen en Verbale Analogieën in de huidige steekproef.

Begrijpend Lezen

Begrijpend lezen is gemeten aan de hand van een test waarin de deelnemer vier tekstfragmenten met elk vijf vragen kreeg (20 vragen in totaal). Deze teksten en vragen zijn ontleed aan voorbeeldexamens van het staatsexamen “Nederlands als tweede taal”. Iedere vraag was multiple-choice, met drie of vier mogelijke antwoorden. In totaal kreeg de kandidaat 15 minuten om de vragen te beantwoorden. Als hij/zij een antwoord niet zeker wist dan kon dit aangegeven worden bij de vraag, om later nog eens bij deze vraag terug te keren. Als uitkomstmaat voor het niveau van begrijpend lezen is simpelweg het aantal goed gegeven antwoorden genomen (M = 15.1, SD = 3.2, Min-Max = 3-20). De test bleek dus redelijk eenvoudig: de meeste deelnemers hadden relatief veel vragen goed. Ongeveer 1% van de kandidaten had echter alle vragen goed beantwoord. De betrouwbaarheid van de begrijpend lezen-test was voldoende (α = .73).

6.5.2.4. Resultaten

In Tabel 6.26. staan de correlaties weergegeven tussen de subtests van de ACT Algemene Intelligentie, de g-score gebaseerd op deze subtests en de begrijpend lezen-score. De correlaties tussen de scores op basis van de ACT Algemene Intelligentie zijn, zoals verwacht, hoog te noemen. Opvallend is wel dat dat verbale capaciteiten, in tegenstelling tot wat vooraf voorspeld was, niet de sterkste relatie met het niveau van begrijpend lezen laat zien: de sterkste relatie is gevonden voor de g-score (r = .60). Mensen met een hogere mate van algemene intelligentie laten dus ook een hoger niveau van begrijpend lezen zien.

Tabel 6.26. Correlaties tussen scores op de ACT Algemene Intelligentie en Begrijpend Lezen.
	g-score	Cijferreeksen	Figurenreeksen	Verbale Analogieën	Begrijpend Lezen
g-score	.90
Cijferreeksen	.79**	.73
Figurenreeksen	.77**	.55**	.72
Verbale Analogieën	.88**	.50**	.53**	.86
Begrijpend Lezen	.60**	.53**	.49**	.50**	.73
** p < .01  (2-zijdig).
Noot. Betrouwbaarheden op de diagonaal, bij ACT Algemene Intelligentie de empirische betrouwbaarheid, bij Begrijpend Lezen Cronbach’s α.

 

Omdat individuele verschillen zoals leeftijd, opleiding en geslacht van invloed kunnen zijn op de mate waarin men begrijpend kan lezen (Overmaat, Roed, & Ledoux, 2002) is er ook een regressieanalyse uitgevoerd waarbij gekeken is naar het effect van de g-score, wanneer rekening gehouden wordt met deze drie variabelen. Controleren voor leeftijd, opleiding en geslacht had nauwelijks tot geen effect op het effect van intelligentie zoals gemeten door de g-score van de ACT Algemene Intelligentie en begrijpend lezen (β = .59, p < .001).

6.5.2.5. Conclusie en discussie

In dit onderzoek is aangetoond dat intelligentie, gemeten door de ACT Algemene Intelligentie, zoals verwacht, sterk samenhangt met scores op een begrijpend lezen-test. Opvallend was wel dat de verbale capaciteiten van een persoon niet de sterkste invloed hadden op het vermogen tot begrijpend lezen; de sterkste relatie werd gevonden voor algemene intelligentie. Zoals aangegeven in de Introductie is dit echter ook weer niet heel verwonderlijk: algemene intelligentie is met name de bekwaamheid om in probleemsituaties de juiste verbanden te leggen en voor nieuwe, onbekende problemen met oplossingen te komen – deze bekwaamheid zal ook belangrijk zijn bij het oplossen van problemen in begrijpend lezen-tests.

Gezien het feit dat de relaties tussen alle scores op de ACT Algemene Intelligentie en begrijpend lezen sterk waren, draagt dit onderzoek bij aan de begripsvaliditeit van de ACT Algemene Intelligentie.

6.6. Divergente en convergente validiteit: relaties met persoonlijkheid

6.6.1. Inleiding

 Het is een bekend gegeven uit de literatuur dat persoonlijkheid en intelligentie over het algemeen geen duidelijke relatie met elkaar hebben, of in ieder geval tot verschillende domeinen behoren (zie bijvoorbeeld Chamorro-Premuzic & Furnham, 2005). In onderzoeken worden dan ook vaak niet-significante correlaties tussen de twee constructen gevonden (zie bijvoorbeeld Eysenck, 1994). Om deze discriminante validiteit aan te tonen hebben we de personen naast de ACT Algemene Intelligentie ook een korte persoonlijkheidsvragenlijst laten invullen, waarna we de relatie tussen persoonlijkheid en intelligentie (de θ’s) hebben onderzocht.

Tegenwoordig is de overheersende theorie in onderzoek naar persoonlijkheid het ‘Five Factor Model’ (FFM; Allport & Odbert, 1936; Cattell, 1943). Deze theorie wordt ook wel de ‘Big Five’ genoemd (Goldberg, 1981). De theorie van het FFM stelt dat er vijf hoofdfactoren of dimensies zijn van persoonlijkheidstrekken waarop mensen van elkaar kunnen verschillen en met elkaar kunnen worden vergeleken. De vijf factoren van het FFM zijn (Allport & Odbert, 1936; Cattell, 1943):

1. Extraversie (Extraversion)
2. Vriendelijkheid (Agreeableness)
3. Zorgvuldigheid (Conscientiousness)
4. Neuroticisme (Neuroticism)
5. Openheid / Cultuur/ Intellect /Autonomie (Openness to experience)

6.6.2. Hypothesen

Op basis van eerdere bevindingen verwachten we lage correlaties met de Big Five persoonlijkheidskenmerken. Van de Big Five kenmerken worden soms wat hogere correlaties gevonden tussen intelligentie en de factor Openheid, omdat Openheid ook een cognitieve/creatieve component bevat (zie bijv. Ashton, Lee, Vernon, & Jang, 2000; DeYoung, Peterson, & Higgins, 2005; Moutafi, Furnham, & Crump, 2006). Zoals uit de terminologie van de Big Five hierboven al op te maken valt, is – in ieder geval een deel – van Openheid gerelateerd aan Intellect. Op basis hiervan verwachten wij ook een wat hogere (c.q. significante) correlatie tussen intelligentie en de factor Openheid.

6.6.3. Steekproef

Dit onderzoek is uitgevoerd op de steekproef waarbij ook de soortgenotenvaliditeit is onderzocht (N = 92; zie sectie 6.5.1.).

6.6.4. Instrumenten

In ons onderzoek hebben we de Nederlandse versie van de Big Five Inventory (BFI; Denissen, Geenen, Van Aken, Gosling, & Potter, 2008) gebruikt om de Big Five persoonlijkheidskenmerken te meten. Deze vragenlijst bestaat uit 44 items waarvan aangetoond is dat de psychometrische kwaliteiten goed zijn (Denissen et al., 2008). De vragen zijn gesteld in een 5-punts Likert format (1 = Helemaal oneens; 5 = Helemaal eens).

Als maat voor intelligentie hebben de proefpersonen de ACT Algemene Intelligentie voltooid (zie voor meer informatie over de procedure en betrouwbaarheden sectie 6.5.1.).

6.6.5. Resultaten

In Tabel 6.27. staan de correlaties tussen de Big Five en de scores op basis van de drie subtests van de ACT Algemene Intelligentie en de hierop berekende g-score.

Tabel 6.27. Correlaties tussen ACT Algemene Intelligentie en Big Five persoonlijkheidskenmerken (N = 92).
		1	2	3	4	5	6	7	8	9
1	g-score	1
2	Cijferreeksen	.84**	1
3	Figurenreeksen	.83**	.63**	1
4	Verbale Analogieën	.90**	.60**	.63**	1
5	Extraversie	-.06	.06	-.19	-.06	.81
6	Vriendelijkheid	-.08	-.06	-.14	-.04	.25*	.76
7	Zorgvuldigheid	-.07	-.11	-.15	.01	.13	.29**	.76
8	Neuroticisme	-.03	-.04	.06	-.03	-.42**	-.36**	-.36**	.88
9	Openheid	.28**	.23*	.17	.28**	.15	.11	.01	-.16	.76
* p < .05  (2-zijdig), ** p < .01  (2-zijdig).
Noot. Betrouwbaarheden op de diagonaal.

Zoals verwacht zijn de correlaties met de persoonlijkheidskenmerken over het algemeen laag. Voor Extraversie, Vriendelijkheid, Zorgvuldigheid en Neuroticisme geldt dat de gevonden relaties laag en niet significant zijn – dit geldt zowel voor scores op basis van de subtests en de g-score. Wanneer we de richtlijnen volgen van Cohen (1988; .10 = klein effect, .30 = gemiddeld effect, .50 groot effect) kunnen deze effecten als ‘klein’ geclassificeerd worden. Interessant is dat, zoals voorspeld, de relatie tussen intelligentie en Openheid het hoogst en wel significant is. Ook deze relatie is echter te kwalificeren als een relatief klein tot gemiddeld effect.

Om na te gaan in hoeverre intelligentie zoals gemeten met de ACT Algemene Intelligentie en persoonlijkheid – dus alle Big Five persoonskenmerken gezamenlijk – overlappen zijn er regressieanalyses uitgevoerd met steeds een ACT-score (Cijferreeksen, Figurenreeksen, Verbale Analogieën en de g-score) als afhankelijke variabele en de Big Five als onafhankelijke variabelen. De verklaarde variantie (R²) van persoonlijkheid in de verklaring van scores op Cijferreeksen, Figurenreeksen, Verbale Analogieën en de g-score was 7%, 10%, 9% en 10%: al deze percentages waren niet significant. Dit duidt aan dat persoonlijkheid en intelligentie, zoals gemeten met de ACT Algemene Intelligentie, niet aan elkaar gerelateerd zijn.

6.6.6. Conclusie relatie intelligentie – persoonlijkheid

Op basis van dit onderzoek kunnen we concluderen dat er bewijs is voor discriminante validiteit van de ACT Algemene Intelligentie in relatie met persoonlijkheid. De relatie tussen de ACT Algemene Intelligentie en Openheid was voorspeld op basis van de literatuur, en dit ondersteunt dan ook de begripsvaliditeit van de test. Ook dit biedt weer bewijs voor het feit dat de ACT Algemene Intelligentie het beoogde concept, intelligentie, lijkt te meten.

6.7. Convergente validiteit: relaties met reactietijden

Begripsvalidering is nooit af (Cotan, 2009): dat wil zeggen dat een test niet eenvoudigweg als ‘begripsvalide’ gezien kan worden maar dat verschillende onderzoeken samen optellen tot bewijs voor begripsvaliditeit. Daarom hebben wij in deze handleiding ook een onderzoek opgenomen over de relaties tussen scores op de ACT Algemene Intelligentie en reactietijden, hoewel dit op het eerste oog gezien het beoogde testdoel (selectie van personeel) van de test misschien niet heel relevant lijkt. Echter, het feit dat eerder aangetoonde relaties tussen intelligentie en reactietijden ook kunnen worden aangetoond met de ACT Algemene Intelligentie kan gezien worden als aanvullend bewijs voor begripsvaliditeit van de test. Bovendien worden de scores op de reactietijdentests uit het huidige onderzoek gebruikt in een selectieprocedure, wat de praktische relevantie van deze resultaten aangeeft.

6.7.1. Inleiding

De relatie tussen intelligentie en reactievermogen is vaak onderzocht maar met wisselende resultaten. Khodadadi et al. (2014) bespreken in hun literatuuroverzicht verschillende onderzoeken naar de samenhang tussen intelligentie en reactietijden. In sommige van deze onderzoeken is er geen relatie gevonden terwijl in jet merendeel van de  andere onderzoeken zwakke tot gemiddelde negatieve correlaties zijn gevonden (van lager dan -.20 tot -.50). Khodadadi et al.  verklaren deze verschillen onder andere door de uiteenlopende meetinstrumenten en verschillende interpretaties van intelligentie en, met name, reactietijd in de verschillende onderzoeken.

Voor het meten van het reactievermogen worden verschillende typen reactietijdtaken gebruikt (Kosinkski, 2008). Zo zijn er simpele reactietijdtaken waarbij de taak van de proefpersoon is om na het waarnemen van een stimulus zo snel mogelijk te reageren (meestal door op een knop te drukken). Dan zijn er ook nog recognition taken, waarbij niet op iedere stimulus gereageerd dient te worden, maar slechts op een bepaalde subset van stimuli. Ten slotte zijn er de choice reactietijdtaken. Hierbij moet een andere reactie worden gegeven afhankelijk van de stimulus. Meestal houdt dit in dat de proefpersoon voor de ene subset van stimuli op de ene knop moet drukken en voor een andere subset op een andere. Donders (1868) observeerde, in een van de eerste laboratoriumonderzoeken naar reactietijden, al dat de reactietijd langer was naarmate taken complexer werden. Hij concludeerde dat er bij de complexere taken sprake moest zijn van een mentaal proces. Op dit mentale proces ligt ook meestal de nadruk wanneer er gesproken wordt over de samenhang tussen intelligentie en reactietijden.

De verklaringen die gegeven worden voor de samenhang tussen intelligentie en reactievermogen richten zich over het algemeen op een (fysieke) onderliggende factor die invloed heeft op zowel het reactievermogen als intelligentie (Deary et al., 2001). Zo noemen Schmiedek et al. (2007) aandachtsverslapping als een mogelijke factor terwijl Jensen (1993) verwerkingssnelheid of ‘neuronale oscillatie’ als mogelijke oorzaken noemt. Dat een hogere neuronale verwerkingssnelheid samenhangt met een beter reactievermogen is eenvoudig te verklaren: Hoe sneller een prikkel verwerkt wordt hoe sneller een reactie op een stimulus geproduceerd kan worden. Daarnaast zal een hogere verwerkingssnelheid ook leiden tot een betere prestatie op intelligentietests: aan de ene kant omdat intelligentietests vaak werken met een tijdslimiet waarin de opdrachten gemaakt moeten worden en snelheid dus een rol speelt, aan de andere kant omdat een hogere verwerkingssnelheid zorgt voor meer beschikbare capaciteit in het werkgeheugen.

Op basis van de theorie dat er een algemene factor is die zorgt voor betere prestaties qua reactietijd én intelligentie is te verwachten dat er een negatieve relatie is tussen gemiddelde reactietijd en intelligentie.

Over het algemeen wordt aangenomen dat er bij complexere taken sprake is van een sterkere mentale component. Jensen (1993) geeft aan dat dit effect van complexiteit ook regelmatig in de literatuur is gerapporteerd. Daarnaast geeft hij aan dat deze correlatie sterker is naarmate de intelligentietest vooral de algemene factor g meet. Dit leidt tot de verwachting dat in het huidige onderzoek de correlaties tussen intelligentie en de gemiddelde reactietijd sterker zullen zijn voor de choice reactietijdtaak dan voor een simpele reactietijdtaak én dat de correlaties hoger zullen zijn naarmate de subtest een hogere mate van de algemene factor g meet.

6.7.2. Methoden

6.7.2.1. Deelnemers

De deelnemers zijn 923 personen die hebben deelgenomen aan een testdag voor toelating tot een chauffeursopleiding. Van deze groep was 91.2% man, de gemiddelde leeftijd was 37.1 (SD = 11.2, Min.-Max. 18-61, van 5 personen was de leeftijd onbekend). De opleidingsniveaus van de personen in de steekproef zijn weergegeven in Tabel 6.28.

Mannen zijn overduidelijk oververtegenwoordigd in de steekproef; we hebben echter genoeg vrouwen in de steekproef om voor geslacht te kunnen controleren bij de analyses. Qua opleidingsniveau hebben de meeste kandidaten een MBO niveau: gelet op het aantal kandidaten in de andere categorieën kunnen we echter voldoende spreiding verwachten in zowel intelligentie als reactietijden. Dit blijkt ook uit Tabel 6.29. en Tabel 6.30. We schatten daarom in dat de kenmerken van de steekproef geen grote invloed heeft uitgeoefend op de resultaten.

Tabel 6.28. Verdeling opleidingsniveaus in steekproef.
	Freq.	%
Lagere school/basisonderwijs	23	2.5
VMBO	133	14.4
MBO	670	72.6
HAVO	30	3.3
VWO	8	.9
HBO	35	3.8
WO	6	.7
Onbekend	2	.2
Anders	16	1.7
Totaal	923	100

6.7.2.2. Instrumenten

Voor het meten van intelligentie wordt de ACT Algemene Intelligentie gebruikt. Als uitkomstmaten wordt zowel gebruik gemaakt van de θ-scores op de subtests als van de g-score.

Reactietijd

 Voor het meten van de reactietijden is de Reactietijdentest van Ixly gebruikt. Deze test bestaat uit twee onderdelen van elk ongeveer 10 minuten.

Deel 1 betreft een simpele reactietijdtaak. De kandidaat ziet een afbeelding met daarop verschillende, gekleurde figuren. Tijdens de test vindt steeds een verandering plaats, een nieuw figuur verschijnt of (een deel van) een figuur verdwijnt. Het is aan de kandidaat om na het zien van de verandering zo snel mogelijk op een knop te drukken. Na iedere opdracht ontvangt de kandidaat feedback. Ofwel hoe snel zijn/haar reactietijd was, ofwel een melding dat de kandidaat de verandering gemist heeft.

Figuur 6.5. Voorbeeldopgave Reactietijdtaak 1

Deel 2 betreft een choice reactietijdtaak. De kandidaat ziet een scherm met daarop een aantal simpele zwarte symbolen. Tijdens de taak verschijnen er nieuwe symbolen of verdwijnen er symbolen. De kandidaat moet enkel reageren wanneer het zojuist verschenen symbool een pijltje naar links of rechts is. Afhankelijk van de richting die de pijl op wijst moet zo snel mogelijk een bepaalde knop ingedrukt worden. Ook hier krijgt de kandidaat feedback over de snelheid en juistheid van de reactie.

Figuur 6.6. Voorbeeldopgave Reactietijdtaak 2.

Als uitkomstmaat wordt de gemiddelde reactietijd (uitgedrukt in ms) van elk van de twee tests genomen. In deze steekproef werd een significante correlatie gevonden van .39 tussen de twee reactietijdtaken. Aangezien de twee taken voorbeelden zijn van verschillende type reactietijdtaken is te verwachten dat er een correlatie als deze wordt gevonden. De tests meten immers beiden reactietijd, maar niet op exact dezelfde manier, waardoor beide tests dus voor een deel verantwoordelijk zullen zijn voor unieke variantie in het reactievermogen van personen.

Ook zijn er een aantal foutmaten als uitkomstmaten gebruikt. Bij de eerste reactietijdtest is dit het aantal keer dat men ‘te laat’ heeft gedrukt; wanneer de kandidaat niet binnen de 1500 ms gedrukt heeft dan wordt dit als fout gerekend. Bij de tweede reactietijdtest is deze maat ook gebruikt. Een tweede maat (‘Onterecht gedrukt’) is het aantal keer dat de kandidaat gedrukt heeft zonder dat dit nodig was (omdat er geen rood pijltje verscheen maar een ander symbool waarbij de kandidaat niet moest drukken). De derde maat (‘Verkeerde toets’) was het aantal keer dat de kandidaat het linke pijltje indrukte terwijl het rechter pijltje ingedrukt moest worden en andersom. Door een fout in het testsysteem werd bij de tweede test aan het begin van de testperiode niet de juiste reden van een fout opgeslagen. Vandaar dat deze informatie beschikbaar is voor 729 kandidaten.

6.7.2.3. Procedure

Meer informatie over de procedure is te vinden in sectie 6.5.2.2. Voor dit onderzoek wordt alleen gebruik gemaakt van de resultaten van de ACT Algemene Intelligentie en de reactietijdtaken.

Omdat er in de literatuur verschillen worden gevonden op basis van geslacht (waarbij vrouwen iets langzamer lijken te reageren op stimuli; Dane & Erzurumlugoglu, 2003; Der & Deary, 2006; Kosinki, 2008) en leeftijd (waarbij reactietijd lijkt toe te nemen met leeftijd; Der & Deary, 2006; Jevas & Yan, 2001; Kosinki, 2008) hebben we ervoor gekozen te controleren voor deze twee variabelen. De resultaten worden in de volgende sectie toegelicht.

6.7.3. Resultaten

In Tabel 6.29. zijn de gemiddelden en standaarddeviaties van de scores op de ACT Algemene Intelligentie weergegeven bij deze steekproef. De scores op zowel de ACT Algemene Intelligentie en de twee reactietijdtaken liggen op alle onderdelen rondom of net iets onder het populatiegemiddelde. Dit is passend gezien de steekproef die voornamelijk bestaat uit mensen met een MBO werk- en denkniveau (zie ook Hoofdstuk 4 voor de gemiddelde scores bij de MBO normgroep).

Tabel 6.29. Gemiddelde θ-scores en standaarddeviaties van de ACT Algemene Intelligentie
	Gem.	SD
Cijferreeksen	-.12	.70
Figuurreeksen	.02	-.75
Verbale Analogieën	-.04	.76
g-score	-.06	.60

In Tabel 6.30. is te zien dat, zoals te verwachten is, de gemiddelde reactietijd en de spreiding groter zijn bij de tweede, complexere taak, dan bij de simpele reactietijdtaak.

Tabel 6.30. Gemiddelde reactietijd en spreiding van reactietijden
	Gem.   reactietijd	SD   reactietijd
Simpele reactietijdtaak (Taak 1)	423.73 ms	91.25 ms
Choice reactietijdtaak (Taak 2)	678.08 ms	149.34 ms

Om de samenhang tussen de ACT Algemene Intelligentie (onderdelen) en de reactietijdtaken te onderzoeken is een Pearson correlatie berekend tussen de θ-scores van de ACT Algemene Intelligentie en de gemiddelde reactietijd op de twee reactietijdtaken. Tabel 6.31. laat de resultaten van deze analyses zien. Tussen de scores op alle onderdelen van de ACT Algemene Intelligentie en de beide reactietijdtests zijn zwakke negatieve correlaties te zien. Alle gevonden correlaties zijn significant, de meeste op p <.01 niveau.

Door middel van lineaire regressie is de relatie tussen de ACT Algemene Intelligentie en reactietijd onderzocht, controlerend voor het effect van geslacht en leeftijd. Alle effecten uit Tabel 6.31. bleven praktisch onveranderd. Bij de eerste reactietijdtest bleek er geen effect van geslacht. Bij de tweede reactietijdtest hadden vrouwen een iets hogere reactietijd (βs tussen de .08 en .10): hiermee werden eerdere bevindingen uit de literatuur dus bevestigd (zie bijvoorbeeld Der & Deary, 2006). Bij beide reactietijdtaken, maar sterker bij de tweede (Taak 1: βs tussen de .12 en .17; Taak 1: βs tussen de .47 en .51), bleek dat leeftijd een positief effect had op reactietijd; zoals al vaker is bevestigd in de literatuur (zie bijvoorbeeld Der & Deary, 2006, Reimers & Maylor, 2005 en Tun & Lachman, 2008) lijkt reactievermogen dus af te nemen met leeftijd.

Tabel 6.31. Correlaties tussen scores op de ACT Algemene Intelligentie en gemiddelde reactietijd.
	Simpele reactietijdtaak	Choice reactietijdtaak
	(Taak 1)	(Taak 2)
Cijferreeksen	-.18**	-.14**
Figuurreeksen	-.21**	-.22**
Verbale analogieën	-.22**	-.07*
g-score	-.25**	-.15**
** p < .01, * p < .05

In Tabel 6.32. staan de correlaties weergegeven tussen de scores op de ACT Algemene Intelligentie en de foutmaten. Alle correlaties zijn significant. Verder zijn er niet veel verschillen te ontdekken in de correlaties met de verschillende foutmaten.

Interessant om op te merken was dat de maten ‘Aantal keer te laat’ en ‘Verkeerde toets’ slechts een zwakke correlatie lieten zien met elkaar (r = .07, p = .05), de maten ‘Aantal keer te laat’ en ‘Onterecht gedrukt’ een middelmatige (r = .21, p = .00) en ‘Verkeerde toets’ en ‘Onterecht gedrukt’ een relatief sterke (r = .45, p = .00). Het leek dus dat de complexiteit van de taak ertoe leidde dat het drukken op de verkeerde toets en onterecht drukken relatief vaak samengingen.[10]

Tabel 6.32. Correlaties tussen scores op de ACT Algemene Intelligentie en foutmaten.
	Taak 1		Taak2
	Aantal keer te laat		Aantal keer te laat	Verkeerde toets	Onterecht gedrukt
Cijferreeksen	-.21**		-.20**	-.21**	-.26**
Figuurreeksen	-.24**		-.30**	-.17**	-.27**
Verbale analogieën	-.19**		-.26**	-.20**	-.26**
g-score	-.24**		-.31**	-.24**	-.31**
** p < .01

6.7.4. Discussie

De resultaten bevestigen de hypothese dat er een negatieve relatie zou bestaan tussen de scores op de ACT Algemene Intelligentie en de gemiddelde reactietijd op beide reactietijdtests. Zowel voor de simpele als de choice reactietijdtaak worden significante negatieve correlaties gezien, zowel met de scores op de subtests als met de g-score van de ACT Algemene Intelligentie.

In eerdere onderzoeken worden zwakke tot gemiddelde negatieve correlaties gerapporteerd (als er significante correlaties gevonden worden) (Khodadadi et al., 2014). De (zwakke) correlaties die in het huidige onderzoek gevonden worden sluiten dus aan bij de resultaten van eerdere onderzoeken naar de relatie tussen intelligentie en reactietijd.

Naast de verwachting dat er negatieve correlaties gevonden zouden worden werd verwacht dat de correlaties op de tweede reactietijdtest (de choice reactietijdtaak) sterker zouden zijn dan die op de eerste (de simpele reactietijdtaak). Deze hypothese werd echter niet bevestigd. Over het algemeen zijn juist minder sterke correlaties te zien op de tweede test.

Dit resultaat is mogelijk het gevolg van methodologisch tekortkomingen van het onderzoek. Hierdoor kan de samenhang tussen intelligentie en reactietijd verstoord/vertekend zijn. Zo werd de choice reactietijdtaak altijd direct na de simpele reactietijdtaak afgenomen. Een kandidaat heeft zich dus al lange tijd moeten concentreren op het moment dat deze tweede test afgenomen wordt. Uit onderzoek blijkt dat de reactietijd trager wordt door mentale vermoeidheid en dat het effect duidelijker is bij complexe taken dan bij simpele (Kosinkski, 2008). Hierdoor zal de vermoeidheid meer meespelen bij de prestatie op de choice reactietijdtaak dan bij de simpele reactietijdtaak. Deze vermoeidheid kan foutvariantie hebben toegevoegd aan de relaties tussen de ACT Algemene Intelligentiescores en prestatiesop de tweede taak wat de correlaties naar beneden gedrukt kan hebben: het kan dus zijn dat de gevonden correlaties in het huidige onderzoek een onderschatting zijn van de ware correlatie tussen scores op de ACT Algemene Intelligentie en de choice reactietijdtaak.

Hoewel we bij de eerste reactietijdtest zien dat de correlatie met de g-score iets hoger is dan de correlaties van de subtests, komt niet duidelijk naar voren dat testscores met een hogere g-lading een sterker effect op reactietijd vertonen. Opvallend is dat dit bij de tweede, complexere reactietijdtest meer het geval is: de hoogste correlatie wordt gevonden voor Figurenreeksen, de test waarvoor verondersteld wordt dat deze de hoogste g-lading heeft (zie Hoofdstuk 1), Bovendien werd de laagste correlatie gevonden voor de subtest (Verbale Analogieën) waarvan we mogen verwachten dat deze het meest beïnvloed wordt door crystallized intelligentie. Een vergelijkbaar patroon zagen we bij het aantal keren dat een persoon te laat was (Tabel 6.32.). Bij de andere twee foutmaten van de tweede reactietijdtaak was dit echter niet het geval.

Samenvattend zijn de relaties die in dit onderzoek worden gevonden vergelijkbaar met de resultaten van eerdere onderzoeken naar de samenhang tussen intelligentie en reactietijd. Dit geeft verdere ondersteuning aan de criteriumvaliditeit van de ACT Algemene Intelligentie.

6.8. Externe structuur: Relaties met achtergrondvariabelen

 Om na te gaan of ACT Algemene Intelligentie-scores een relatie met de achtergrondvariabelen hebben, is er per variabele onderzocht of de gemiddelde scores voor de verschillende categorieën van deze variabelen significant van elkaar verschillen. Het aantonen van verschillen in gemiddelde scores bij de ACT Algemene Intelligentie van groepen waarvan men mag verwachten dat ze verschillen zullen vertonen, levert een bijdrage aan het bewijs voor de begripsvaliditeit van de ACT Algemene Intelligentie.

Door middel van ANOVA-toetsen zijn de verschillen onderzocht. Tevens is de η² berekend als maat voor de effectgrootte bij variabelen met >2 categorieën. Bij beoordeling van de effectgrootten gaan we uit van de richtlijnen van Cohen (1988): voor η² geldt dat > .01 wordt gezien als een klein effect, > .06 als een gemiddeld effect en > .14 een groot effect. Bij variabelen met twee categorieën is Cohen’s d berekend als effectgroottemaat, waarvoor geldt dat .20 wordt beschouwd als een klein effect, .50 als een gemiddeld effect en >.80 als een groot effect (Cohen, 1988).

6.8.1. Verschillen tussen opleidingsniveaus

 Om na te gaan of de intelligentie-scores een relatie met de achtergrondvariabelen hebben, is er voor de variabele opleidingsniveau onderzocht of de gemiddelde scores voor de verschillende categorieën van deze variabelen significant van elkaar verschillen. We kunnen verwachten dat de relatie tussen intelligentie en opleidingsniveau positief is: personen met hogere opleidingsniveaus zullen een hogere intelligentiescore hebben. Op basis van de meta-analyse van Strenze (2007) mogen we een sterk effect verwachten van intelligentie op het behaalde opleidingsniveau (ongeveer r = .46).

6.8.1.1. Resultaten

 In navolging van de voorgaande hoofdstukken hebben we de analyses gedaan op twee datasets:

1. De kandidaatssteekproef. We hebben alleen de scores van de opleidingsniveaus VMBO, MBO, HBO en WO met elkaar vergeleken. Andere opleidingsniveaus bevatten te weinig respondenten om zinvolle uitspraken over te kunnen doen.
2. De totale steekproef. Omdat de opleidingsniveaus een andere indeling kenden bij de kandidaatssteekproef dan bij de kalibratiesteekproef zijn de opleidingsniveaus gecodeerd en ingedeeld in drie categorieën (laag, midden, hoog). Hoe dit precies gedaan is wordt hieronder besproken.

De verdeling over de opleidingsniveaus bij de kalibratiesteekproef is weergegeven in Tabel 6.33. In navolging van het CBS hebben we deze opleidingsniveaus samengevoegd in drie categorieën: laag, midden, en hoog.

Tabel 6.33. Verdeling opleidingsniveaus in kalibratiesteekproef.
	CR		FR		VA		g-score
Opleidingsniveau	Freq.	%	Freq.	%	Freq.	%	Freq.	%	Categorie
Lagere school/basisonderwijs	158	5.8	146	5.7	98	3.9	200	5.3	Laag
VMBO: basisberoepsgerichte leerweg (BB)	281	10.4	318	12.4	185	7.3	391	10.4	Laag
VMBO: kaderberoepsgerichte leerweg (KB)	144	5.3	143	5.6	87	3.4	187	5.0	Laag
VMBO: Gemengde leerweg (GL)	165	6.1	148	5.8	95	3.7	204	5.4	Laag
VMBO: Theoretische leerweg (TL)	125	4.6	159	6.2	189	7.4	236	6.3	Midden
HAVO	196	7.2	165	6.4	207	8.1	283	7.6	Midden
VWO	98	3.6	81	3.2	79	3.1	112	3.0	Hoog
MBO 1: Assistent beroepsbeoefenaar	77	2.8	68	2.7	55	2.2	100	2.7	Laag
MBO 2: Medewerker	181	6.7	195	7.6	214	8.4	294	7.9	Midden
MBO 3: Zelfstandig medewerker	221	8.2	214	8.3	236	9.3	335	8.9	Midden
MBO 4: Middenkaderfunctionaris	392	14.5	393	15.3	407	16.0	595	15.9	Midden
HBO: Oude stijl	205	7.6	168	6.5	222	8.7	253	6.8	Hoog
HBO: Bachelor	195	7.2	149	5.8	199	7.8	228	6.1	Hoog
HBO: Master	65	2.4	46	1.8	68	2.7	78	2.1	Hoog
WO: Bachelor	57	2.1	44	1.7	55	2.2	70	1.9	Hoog
WO: Master	70	2.6	67	2.6	72	2.8	89	2.4	Hoog
WO: Doctorandus	53	2.0	38	1.5	57	2.2	62	1.7	Hoog
WO: Doctor	8	.3	6	.2	7	.3	8	.2	Hoog
Onbekend	16	.6	18	.7	13	.5	20	.5
Totaal	2707	100	2566	100	2545	100	3745	100.0

De verdeling over de opleidingsniveaus bij de kandidaatssteekproef is weergegeven in Tabel 6.34. In de laatste kolom staat weer aangegeven in welke categorie elke opleidingsniveau is ingedeeld. De representativiteit van deze verdeling is helaas niet te beoordelen omdat het CBS de opleidingsniveaus basisberoepsgerichte en kaderberoepsgerichte leerwegen van het VMBO samenneemt met het MBO-1 niveau, en omdat zij een splitsing maken in HBO/WO-bachelor enerzijds en HBO/WO-master anderzijds. In ons geval is de verdeling gemaakt tussen HBO en WO anderzijds, ongeacht het bachelor- of master-niveau.

Tabel 6.34. Verdeling opleidings-niveaus in de kandidaatssteekproef.
	Aantal	%	Categorie
VMBO	204	10.1	Laag
MBO	1095	54.0	Midden
HBO	402	19.8	Hoog
WO	327	16.1	Hoog
Totaal	2028	100.0

De indeling in de laatste kolommen van Tabel 6.33. en Tabel 6.34. zijn gebruikt om tot een indeling in drie categorieën te komen voor de totale steekproef. De verdeling over de drie categorieën voor de totale steekproef is weergegeven in Tabel 6.35. Deze verdeling was voldoende representatief vergeleken met de beroepsbevolking in 2013 (χ² = 97.15, df = 2, p = .00, Cramer’s V = .09, duidend op een klein verschil). Er bevonden zich iets teveel middelbaar opgeleiden in de huidige steekproef, en iets te weinig hoger opgeleiden.

Tabel 6.35. Verdeling opleidingsniveaus in categorieën in totale steekproef.
	CR		FR		VA		g-score
Categorie	Freq.	%	Freq.	%	Freq.	%	Freq.	%
Laag	1027	19.6	1026	20.1	723	14.7	1286	20.5
Midden	2209	42.2	2217	43.5	2344	47.7	2838	45.2
Hoog	1479	28.3	1328	26.1	1328	27.1	1629	26.0
Onbekend	516	9.9	521	10.2	514	10.5	524	8.3
Totaal	5231	100.0	5092	100.0	4909	100.0	6277	100.0

Totale steekproef

 Een ANOVA-toets wees uit dat de gemiddelde Cijferreeksen-scores tussen opleidingsniveaus significant van elkaar verschilden (F(2,4712) = 202.87, p = .00). Een post-hoc Tukey test wees uit dat middelbaar opgeleiden significant hoger scoorden (M = -.12, SD = .82) dan lager opgeleiden (M = -.34, SD = .94), terwijl hoger opgeleiden weer significant hoger (M = .32, SD = .89) scoorden dan deze twee groepen. De effectgrootte (η² = .079) duidde op een gemiddeld tot sterk effect van opleidingsniveau op de scores op de Cijferreeksentest.

De groepen kandidaten met de drie opleidingsniveaus verschilden van elkaar wat betreft hun Figurenreeksen-score (F(2,4568) = 291.89, p = .00). Een post-hoc Tukey test wees uit dat middelbaar opgeleiden significant hoger scoorden (M = -.10, SD = .77) dan lager opgeleiden (M = -.40, SD = .85) en hoger opgeleiden weer hoger scoorden dan middelbaar opgeleiden (M = .39, SD = .85). De η² was .113, dus het effect van opleiding was redelijk sterk te noemen bij de scores op de Figurenreeksentest.

Een ANOVA-toets wees verder uit dat de gemiddelde Verbale Analogieën-scores verschilden van elkaar op basis van opleidingsniveau (F(2,4392) = 403.56, p = .00). Een post-hoc Tukey test toonde aan dat middelbaar opgeleiden hoger scoorden (M = -.21, SD = .85) dan lager opgeleiden (M = -.53, SD = .85), terwijl hoger opgeleiden significant hoger scoorden dan middelbaar opgeleiden (M = .47, SD = .85). De effectgrootte (η² = .155) duidde op een sterk effect van opleidingsniveau op de scores op de Verbale Analogieëntest.

Tot slot bleek dat de g-scores van de drie groepen significant verschilden (F(2,5750) = 507.58, p = .00). Een post-hoc Tukey test toonde aan dat middelbaar opgeleiden hoger scoorden (M = -.46, SD = .76) dan lager opgeleiden (M = -.15, SD = .78) en hoger opgeleiden weer significant hoger scoorden (M = .37, SD = .74) dan middelbaar opgeleiden. De effectgrootte (η² = .150) duidde op een sterk effect van opleidingsniveau op de g-score van de ACT Algemene Intelligentie.

Kandidaatssteekproef

 De resultaten bij de kandidaatssteekproef vertoonden hetzelfde patroon als bij de totale steekproef. Echter, de verschillen in scores kwamen nog duidelijker naar voren: voor alle tests zagen we dat, zoals verwacht, de VMBO-groep (N = 204) het laagst scoorde, de MBO-groep (N = 1094-1095) hoger, gevolgd door de HBO-groep (N = 402) en de WO-groep (N = 327). Alle ANOVA-toetsen waren significant (Cijferreeksen: F(3,2024) = 186.11, p = .00; Figurenreeksen: F(3,2024) = 149.87, p = .00; Verbale Analogieën: F(3,2024) = 198.00, p = .00; g-score: F(3,2024) = 282.82, p = .00).

Voor zowel de drie subtests als de g-score gold dat de VMBO- en MBO-groep geen significante verschillen lieten zien, hoewel VMBO-ers wel lager scoorden dan MBO-ers. Bij Cijferreeksen scoorden VMBO-ers (M = -.27, SD = .65) en MBO-ers dus ongeveer gelijk (M = -.15, SD = .70). De HBO-groep (M = .42, SD = .77) en de WO-groep (M = .80, SD = .82) scoorden significant hoger dan de VMBO- en MBO-groep. De scores van de HBO- en WO groep verschilden ook significant van elkaar.

Dit patroon van resultaten was hetzelfde voor Figurenreeksen (VMBO: M = -.13, SD = .68, MBO: M = -.05, SD = .76, HBO: M = .42, SD = .76, WO: M = .87, SD = .78), Verbale Analogieën (VMBO: M = -.11, SD = .74, MBO: M = -.02, SD = .76, HBO: M = .63, SD = .66, WO: M = .90, SD = .59) en de g-score (VMBO: M = -.17, SD = .54, MBO: M = -.08, SD = .60, HBO: M = .49, SD = .55, WO: M = .84, SD = .55).

De effectgrootten (η²) duiden voor alle scores op zeer sterke effecten met waarden van .216, .182, .227 en .295 voor respectievelijk Cijferreeksen, Figurenreeksen, Verbale Analogieën en de g-score. Voor de g-score betekent dit omgerekend naar een Pearson correlatie[11] een effect van r = .54. Dit komt goed overeen met de resultaten uit de meta-analyse van Strenze uit 2007 (r = .46). Zie ook Hoofdstuk 7 voor een bevestiging van dit effect in een andere steekproef.

6.8.1.2. Conclusie verschillen in opleidingsniveaus

Met dit onderzoek hebben we aangetoond dat verschillen in intelligentie die we op basis van opleidingsniveau mogen verwachten ook teruggevonden worden bij de ACT Algemene Intelligentie. Dit geeft aan dat verschillen in scores op de ACT Algemene Intelligentie samen lijken te gaan met reële verschillen tussen groepen en dat het beoogde construct – intelligentie – inclusief deze reële verschillen tussen groepen, wordt gemeten. Dit draagt dus bij aan de begripsvaliditeit van de ACT Algemene Intelligentie.

Belangrijk om te vermelden is het feit dat de effectgrootten bij de kandidaatssteekproef duidden op sterke effecten. De totale steekproef bestond ook uit respondenten die maar een deel van de items – en niet adaptief – hebben beantwoord, waarop hun θ berekend is. De ACT Algemene Intelligentie lijkt in reële situaties waarin deze test ingezet wordt zeer goed te kunnen discrimineren op basis van opleidingsniveau.

6.8.2. Verschillen tussen mannen en vrouwen

Over de verschillen tussen mannen en vrouwen in intelligentie is veel onderzoek gedaan, maar zonder eenduidige resultaten. Vanaf het begin van de 20^e eeuw is de consensus lange tijd geweest dat er geen noemenswaardige verschillen tussen volwassen mannen en vrouwen waren in intelligentie (Cattell, 1971; Spearman, 1923; Herrnstein & Murray, 1994). Lynn (1994; 1999) en collegae (Lynn & Irwing, 2004; Irwing & Lynn, 2005) doorbraken deze consensus met een aantal studies waarin aangetoond werd dat jongens en meisjes tot en met 15 jaar inderdaad weinig verschillen op het gebied van intelligentie, maar dat mannen vanaf die leeftijd iets hoger scoren op intelligentietests – het verschil is echter klein, ongeveer zo’n 5 IQ-punten (1/3 SD). Er lijkt wel enig verschil op het niveau van subtests: zo lijken vrouwen iets hoger te scoren op verbale tests dan mannen (zie bijvoorbeeld Hyde & Linn, 1988; Lynn & Kanazawa, 2011; Strand, Deary, & Smith, 2006). Ondanks deze onderzoeken is de consensus tegenwoordig nog steeds dat er nauwelijks noemenswaardig verschillen zijn tussen mannen en vrouwen in hun denkvermogen (zie bijvoorbeeld: Anderson, 2004; Bartholomew, 2004; Halpern, 2000); we verwachten dan ook dat we geen substantiële verschillen zullen vinden tussen scores op basis van de ACT Algemene Intelligentie.

6.8.2.1. Resultaten

 De totale steekproef bestond voor 50.7% uit mannen en 49.3% uit vrouwen. Deze verdeling was voldoende representatief voor de beroepsbevolking (CBS, 2013); hoewel mannen wat ondervertegenwoordigd waren (55% in de beroepsbevolking) was dit verschil klein te noemen (χ² = 45.31, df = 1, p = .00, φ = .05).

Uit Tabel 6.36. komt naar voren dat, zoals voorspeld, de verschillen tussen mannen en vrouwen zeer klein zijn. Kijkend naar de totale steekproef scoorden mannen significant hoger op de Cijferreeksen (t(4921) = 4.95, p = .00), en Figurenreeksen (t(4777) = 4.20, p = .00) dan vrouwen. Ook hadden mannen gemiddeld een iets hogere g-score dan vrouwen (t(5959) = 3.51, p = .00).

Wanneer we echter naar de effectgrootte d kijken en deze vergelijken met de criteria van Cohen (1988), kunnen we stellen dat de verschillen zeer klein tot klein zijn. Met andere woorden, er zijn geen relevante verschillen te vinden tussen mannen en vrouwen op scores op de ACT Algemene Intelligentie.

Bij de kandidaatssteekproef werden alleen significante verschillen gevonden bij scores op de Figurenreeksen (t(2234) = 3.06, p < .01) en Verbale Analogieën (t(2232) = -3.15, p < .01). Interessant om op te merken is dat we bij deze steekproef, net als in de literatuur, terugvinden dat vrouwen iets hoger scoren op de verbale test dan mannen. Gelet op de effectgrootten (rechterkolom Tabel 6.36.) zullen deze verschillen echter niet praktisch relevant zijn. De g-scores verschilden niet van elkaar (t(2234) = -.11, p = .92). Deze kandidaatssteekproef was overigens een redelijke representatie van de beroepsbevolking wat betreft geslacht (χ² = 98.27, df = 1, p = .00, φ = .21, duidend op een ‘gemiddeld’ verschil). In de kandidaatssteekproef bevonden zich naar verhouding iets teveel mannen (65.4% ten opzicht van 55% in de beroepsbevolking).

Tabel 6.36. Verschillen in scores op de ACT Algemene Intelligentie, geslacht.
	Totale steekproef													Kandidaatssteekproefa
	Mannen			Vrouwen						d				Mannen			Vrouwen					d
	N	M	SD	N	M	SD							M		SD	M		SD
Cijferreeksen	2591	.04	.90	2332	-.09	.91			.14**				.12		.82	.06		.85			.08
Figurenreeksen	2513	.03	.88	2266	-.08	.84			.12**				.21		.84	.10		.83			.14**
Verbale Analogieën	2461	-.03	.92	2142	-.06	.94			.03				.20		.82	.31		.84			-.14**
g-score	3020	-.03	.79	2941	-.10	.78			.09**				.17		.68	.17		.71			.00
** p < .01  (2-zijdig).   a Nmannen = 1463, Nvrouwen = 771-773.

6.8.2.2. Conclusie verschillen tussen mannen en vrouwen

De gevonden verschillen zijn grotendeels in overeenstemming met verschillen zoals we konden verwachten op basis van de literatuur: ons onderzoek onderschrijft bijvoorbeeld de consensus dat de gevonden verschillen klein zijn. Bij kleine effecten zullen kenmerken van de steekproef een grotere invloed hebben op de resultaten (in sommige gevallen zal er wel een significant effect gevonden worden, in andere gevallen niet).

In ieder geval kunnen we concluderen dat de kleine verschillen betekenen dat de ACT Algemene Intelligentie goed bij zowel mannen als vrouwen ingezet kan worden en dat er geen duidelijke vertekeningen in de resultaten zullen zijn.

6.8.3. Verschillen tussen leeftijden

Er zijn in de literatuur verschillende hypothesen opgesteld over de relatie tussen leeftijd en intelligentie; ook hier geldt echter weer dat er geen algehele consensus is over deze relatie. Sommigen beargumenteren dat intelligentie over het algemeen niet zoveel fluctueert over de jaren (Schaie, 1983). Een belangrijke distinctie hierbij is echter het onderscheid tussen fluid en crystallized intelligentie: waar verschillen op basis van leeftijd zelfs de theoretische basis vormden (Horn & Cattell, 1966). Over het algemeen wordt aangenomen dat fluid intelligentie haar top kent in de adolescente jaren en dan geleidelijk en steeds sneller afneemt naarmate men ouder wordt (Kaufman & Horn, 1996). Crystallized intelligentie, aan de andere kant, zou weinig tot geen verandering laten zien over de levensloop (Horn & Cattell, 1966, 1967). Echter, anderen voorspelden en hebben laten zien dat bij sommige tests (bijv. vocabulaire tests) er een kleine toename zou kunnen zijn naarmate men ouder wordt (Williams, Myerson, & Hale, 2008), met weer een afname vanaf het 65/70^ste levensjaar (Kaufman & Horn, 1996; Materazzo, 1972).

Op basis van het bovenstaande kunnen we verwachten dat scores op Figurenreeksen, wat de meest zuivere meting van fluid intelligence is, vanaf adolescentie/jong volwassenheid geleidelijk en steeds sneller zullen afnemen. Voor Cijferreeksen en Verbale Analogieën is een voorspelling lastiger te maken omdat deze een mix zullen zijn van fluid en crystallized intelligentie. Omdat we bij Verbale Analogieën de meeste lading op crystallized intelligentie verwachten, voorspellen we dat deze het meest de hypothese zoals hierboven voor crystallized intelligentie zal volgen. Omdat de g-score het oplossen van nieuwe problemen (dus fluid intelligentie) beoogt te meten, verwachten we hier ook een daling met leeftijd vanaf adolescentie/jong volwassenheid, maar minder sterk dan bij Figurenreeksen, omdat er ook voor een deel crystallized intelligentie gemeten wordt.

6.8.3.1. Resultaten

In Tabel 6.37. en Tabel 6.38. worden de verschillen in θ’s tussen de drie leeftijdscategorieën weergegeven voor de totale steekproef en de kandidaatssteekproef. De verschillende leeftijdscategorieën zijn als volgt: Laag (15-24), Midden (25-44) en Hoog (45-67)

Tabel 6.37. Verschillen in scores op de ACT Algemene Intelligentie, leeftijd – totale steekproef.
	Laag			Midden			Hoog				η2
	N	M	SD	N	M	SD	N	M	SD
Cijferreeksen	505	.06	.91	1872	-.06	.94	2143	-.09	.85		.003**
Figurenreeksen	495	.18	.90	1792	.07	.88	2089	-.22	.78		.035**
Verbale Analogieën	477	.03	.93	1754	-.03	.93	1970	-.18	.92		.008**
g-score	596	.05	.80	2207	-.04	.81	2755	-.17	.74		.010**
** p < .01  (2-zijdig).

 

Totale steekproef

De representativiteit van de steekproef wat betreft leeftijd was voldoende (χ² = 131.17, df = 2, p = .00, Cramer’s V = .11, duidend op een klein verschil). Er bevonden zich relatief wat minder personen met een middelbare leeftijd (25-44) in de steekproef ten opzichte van de beroepsbevolking, en wat meer mensen met een hogere leeftijd (45-65).

Op basis van ANOVA-toetsen bleek dat er significante verschillen in scores waren tussen de leeftijdsgroepen voor alle drie de subtests en de ­g-score van de ACT Algemene Intelligentie. Over het algemeen scoorden personen met een hogere leeftijd lager dan mensen met een lagere leeftijd. Een post-hoc Tukey toets wees uit dat bij Cijferreeksen de scores tussen de middelste en hoogste leeftijdscategorie niet significant van elkaar verschilden. De twee overige verschillen (laag-hoog en laag-midden) vertoonden wel significante verschillen in scores. Bij Verbale Analogieën verschilden de scores van jongeren en personen met middelbare leeftijd niet van elkaar – de overige groepen vertoonden (laag-hoog, midden-hoog) wel significante verschillen in scores. Voor Figurenreeksen en de g-score gold dat mensen met middelbare leeftijd significant lager scoorden dan jongere mensen, en dat mensen uit de hoogste leeftijdscategorie weer significant lager scoorden dan deze twee jongere groepen.

Om een idee te krijgen van de relevantie van de verschillen hebben we de effectgrootten η² berekend. Net als voor de verschillen bij geslacht, zijn ook hier de verschillen zeer klein te noemen, wanneer we weer de criteria van Cohen (1988) hanteren.

Kandidaatssteekproef

 In de kandidaatssteekproef bevonden zich naar verhouding te weinig ouderen ten opzichte van de beroepsbevolking, hoewel het hier om een klein verschil ging (χ² = 38.76, df = 2, p = .00, Cramer’s V = .10).

Bij de kandidaatssteekproef werden bij een ANOVA-toets geen significante verschillen gevonden op basis van leeftijd op de scores behaald op de Verbale Analogieëntest. ANOVA-toetsen toonden aan dat er wel een effect van leeftijd was op de scores van de overige twee subtests en de g-score. Bij Figurenreeksen en de g-score scoorden mensen tussen de 45 en 67 significant lager dan beide jongere groepen, terwijl het verschil in scores tussen 25-44 jarigen en 15-24 jarigen niet significant was. Bij Cijferreeksen waren de verschillen tussen alle drie de groepen significant.

Tabel 6.38. Verschillen in scores op de ACT Algemene Intelligentie, leeftijd – kandidaatssteekproef.
	Laag			Midden			Hoog			η2
	M	SD		M	SD		M	SD
Cijferreeksen	.20	.78		.06	.84		-.06	.71		.012**
Figurenreeksen	.32	.86		.23	.85		-.08	.74		.037**
Verbale Analogieën	.19	.89		.18	.83		.21	.79		.000
g-score	.21	.72		.14	.71		.04	.62		.008**
** p < .01  (2-zijdig).   NLaag = 260, NMidden = 933, NHoog = 640.

De effectgrootten (η²) duidden echter weer op zeer kleine effecten van leeftijd op de behaalde scores op de ACT Algemene Intelligentie, met relatief het sterkste effect bij Figurenreeksen.

 Regressieanalyses

Om een gedetailleerder beeld te krijgen van de relatie tussen leeftijd en intelligentie, gemeten door de ACT Algemene Intelligentie, hebben we een serie lineaire regressies uitgevoerd. Hierin hebben we eerst het lineaire effect van leeftijd als voorspeller toegevoegd, en vervolgens leeftijd – de continue variabele – tot steeds hogere machten (dus leeftijd², leeftijd³ et cetera). Voor Cijferreeksen was er een zeer klein negatief lineair effect (B = -.004, p = .00 bij totale steekproef; B = -.009, p = .00 bij kandidaatssteekproef). Voor Figurenreeksen bleek een kwadratische relatie het beste model (toevoegen van leeftijd³ leverde geen verbetering in termen van verklaarde variantie op) bij de totale steekproef en een lineaire relatie (B = -.017, p = .00) bij de kandidaatssteekproef. Voor Verbale Analogieën bleek dit bij beide steekproeven een derdegraadsvergelijking te zijn. Voor de g-score bleek dit een kwadratische functie te zijn in de totale steekproef en een lineaire functie in de kandidaatssteekproef (B = -.007, p = .00). In Figuur 6.7. zijn de relaties weergegeven voor de totale steekproef.

Figuur 6.7. Relatie tussen leeftijd en scores op Figurenreeksen, Verbale Analogieën en g-score in de totale steekproef.

De gevonden relaties bevestigen voor een deel de voorspellingen uit de literatuur. Zo zien we dat scores op de Figurenreeksen, wat de meest zuivere meting van fluid intelligence is, pieken bij jong-volwassenheid en een steeds snellere afname van scores naarmate men ouder wordt. Ook voor de relatie van de g-score, zien we de voorspelde piek in de vroege adolescentie, gevolgd door min of meer een plateau met een afname op latere leeftijd. De g-score weerspiegelt fluid intelligentie en crystallized intelligentie, maar in het geval van de ACT Algemene Intelligentie vooral fluid intelligentie (zie sectie 1.1. en 1.3.).

Op basis van het feit dat Verbale Analogieën voor een deel crystallized intelligence meet, voorspelden we een sterke afname op latere leeftijd. Deze afname zien we hier ook, hoewel dit wel al veel eerder is (ongeveer rond de 38 jaar) dan de 65/70 jaar die Kaufman en Horn (1996) en Matarazzo (1972) noemen. Bovendien zien we in deze steekproef geen aanvankelijke stijging: vanaf de adolescentie daalt het intelligentieniveau, alleen in meer of mindere mate. In de kandidaatssteekproef was dit echter anders, zoals duidelijk wordt uit Figuur 6.8.

Figuur 6.8. Relatie tussen leeftijd en Verbale Analogieën in de kandidaatssteekproef.

De relatie zoals weergegeven in Figuur 6.8. is meer conform de hiervoor beschreven hypothese: een aanvankelijke toename met een uiteindelijke afname op latere leeftijd (ongeveer rond de 49 jaar). De eerste daling tussen de 17 en ongeveer 28 jaar is echter niet zoals voorspeld door de literatuur.

Over het algemeen kunnen we echter concluderen dat de verschillen, wanneer we alle vier de figuren in beschouwing nemen, klein zijn.

6.8.3.2. Conclusies verschillen in leeftijd

 Op basis van het hierboven beschreven onderzoek kunnen we concluderen dat de scores op de ACT Algemene Intelligentie en zijn subtests reële verschillen in leeftijd weerspiegelen, wat bewijs biedt voor de begripsvaliditeit van het instrument. Een kanttekening bij de resultaten van de regressieanalyses is dat deze gebaseerd zijn op cross-sectionele data: om meer solide conclusies over de relaties tussen de scores op de ACT Algemene Intelligentie en leeftijd te kunnen trekken zou er longitudinaal onderzoek gedaan moeten worden. Ook het feit dat men het oneens is over wat de relatie is tussen leeftijd en intelligentie, maakt het trekken van conclusies hierover moeilijk.

Bovenal kunnen we concluderen dat de verschillen tussen leeftijdsgroepen zeer klein zijn: de ACT Algemene Intelligentie kan dus goed ingezet worden bij personen van alle leeftijden.

6.8.4. Verschillen tussen autochtonen en allochtonen

Zoals in Hoofdstuk 1 beschreven worden er vaak verschillen gevonden in scores tussen autochtonen en allochtonen, en dan met name bij verbale tests (Van den Berg & Bleichrodt, 2000). De effectgrootten bij volwassenen lopen sterk uiteen (ongeveer variërend tussen de .2 en 2; Te Nijenhuis & Van der Flier, 1997; Van den Berg, 2001; Van den Berg & Bleichrodt, 2000; Verouden, Ross, Stet, & Scheele, 1987), maar hier speelt dus onder andere het soort test een rol. Andere belangrijke factoren die de grootte van de verschillen beïnvloeden zijn de generatie (1^e of 2^e), herkomstgroep (bijvoorbeeld Turks of Surinaams), taalvaardigheid, verblijfsduur in Nederland en het wel/niet hebben gevolgd van het Nederlands basisonderwijs, waarbij een deel van deze factoren onderling ook samenhangen: hoe langer iemand in Nederland verblijft, hoe beter over het algemeen de kennis van de Nederlandse taal is (Te Nijenhuis, De Jong, Evers en Van der Flier, 2004).

Doordat er veel verschillende oorzaken aan de verschillen te grondslag liggen is het niet eenvoudig een eenduidige uitspraak te doen over de verwachte verschillen. Uit onderzoek van Van den Berg (2001) en Van den Berg en Bleichrodt (2000) met de MCT-tests bleek dat het verschil bij eerstegeneratieallochtonen 1.2 standaarddeviaties was, en bij tweede-generatieallochtonen +0.1 tot 0.38. Gezien bij deze test sterk de nadruk is gelegd op het minimaliseren van verschillen tussen autochtonen en allochtonen, kunnen deze waarden als een goed criterium genomen worden. In een overzichtsartikel uit 2004 stellen Te Nijenhuis, De Jong, Evers en Van der Flier dat voor eerstegeneratieallochtonen (Turken, Marokkanen, Surinamers en Antillianen) het verschil ongeveer 1.13 standaarddeviaties is, en voor tweede-generatieallochtonen (voor dezelfde vier groepen) ongeveer .71 standaarddeviatie. We lijken dus effectgrootten ergens tussen de waarden van Van den Berg (2001) en Van den Berg en Bleichrodt (2000) en Te Nijenhuis et al. (2004) verwachten.

6.8.4.1. Resultaten

In de inleiding hebben we al uiteengezet dat de subtests van de ACT Algemene Intelligentie verschillen in de mate waarin de items cultuurvrij zijn, waarbij de Figurenreeksen het meest cultuurvrij te noemen is. Om dit empirisch te onderzoeken hebben we gekeken naar het verschil in θ’s tussen autochtonen en allochtonen. Gezien het feit dat de Figurenreeksen cultuurvrij zou moeten zijn, verwachten we dat er geen noemenswaardige verschillen zijn in de θ van deze twee groepen zoals gemeten door de Figurenreeksen. Dit hebben we afgezet tegen verschillen in θ’s gebaseerd op de Verbale Analogieën en Cijferreeksen tests: gezien het feit dat deze respectievelijk meer verbale en aangeleerde kennis meten, kunnen we verwachten dat hier de verschillen groter zijn.

Er zijn op dit moment drie verschillende steekproeven waarin we informatie hebben over etniciteit en waar we dus vergelijkingen tussen autochtonen en allochtonen kunnen maken. De eerste is de kalibratiesteekproef (zie Hoofdstuk 1). De tweede is een steekproef uit de Ixly database (N = 284, waarvan 94 personen (32%) allochtoon), verzameld tussen juli en november 2016. De derde is een samengestelde steekproef uit de eerste en tweede steekproef: omdat de tweede steekproef bij een vrij specifieke groep is verzameld (namelijk bij één bedrijf dat personen wierf voor een leer- en werktraject in de transportsector), en de N relatief klein is, hebben we de data samengevoegd met de kalibratiesteekproef. We rapporteren alleen de resultaten van de tweede en derde steekproef omdat de resultaten van de eerste en derde steekproef nauwelijks van elkaar verschilden.

Voor de definitie van ‘allochtoon’ hanteren wij dezelfde als het CBS: iemand wordt als allochtoon gedefinieerd wanneer die persoon zelf of één van beide ouders in het buitenland geboren is (CBS, 2000).[12] Voor de definitie van de herkomstgroepering gebruiken wij ook de definitie van het CBS (2013): van een in het buitenland geboren allochtoon wordt zijn of haar geboorteland beschouwd als het land van herkomst. Van een in Nederland geboren allochtoon wordt het geboorteland van de moeder beschouwd als het land van herkomst, indien de moeder niet in Nederland is geboren. Indien zowel de persoon als diens moeder in Nederland zijn geboren, dan wordt het geboorteland van de vader beschouwd als het land van herkomst.

Tabel 6.39. Verdeling herkomstgroepen allochtonen gemengde steekproef.
	Freq.	%
Afrika (exclusief Marokko)	20	3.7
Azië (inclusief (voormalig) Indonesië, Australië)	122	22.8
Europa (exclusief Nederland, inclusief (voormalig) Joegoslavië)	176	32.9
Marokko	35	6.5
Nederlandse Antillen / Aruba	56	10.5
Suriname	60	11.2
Turkije	36	6.7
Noord-Amerika (V.S., Canada)	14	2.6
Zuid-Amerika (exclusief Suriname)	16	3.0
Totaal	535	100

In 2013 bestond ongeveer 19.0% van de beroepsbevolking uit personen van allochtone herkomst (CBS, 2013). In de gemengde steekproef bevonden zich 13.3% allochtonen. Vergeleken met CBS gegevens van 2013 was deze steekproef niet geheel representatief voor de Nederlandse beroepsbevolking wat betreft geslacht (χ² = 83.30, df = 1, p = .00). De effectgrootte φ duidde echter aan dat het verschil als klein tot gemiddeld gekwalificeerd kon worden (φ = .14). We kunnen dus concluderen dat het aantal allochtonen in de steekproef voldoende representatief was in vergelijking met de beroepsbevolking.

Wat betreft de herkomst van de allochtonen in de gemengde steekproef bleek 4.7% van de totale steekproef bestond uit personen met een ‘traditionele’ achtergrond wat betreft herkomstgroepering (Suriname, Nederlandse Antillen/Aruba, Turkije en Marokko), in de beroepsbevolking was dit 6.8%. Hoewel deze percentages significant van elkaar afweken (χ² = 29.79, df = 1, p = .00), uitgedrukt in effectgrootte φ was de relevantie van dit effect klein (.09).

Ten opzichte van het aantal allochtonen bestond 35.0% uit de ‘traditionele’ groepen in de huidige steekproef, ten opzichte van 33.8% in de beroepsbevolking (2013). Deze aantallen verschilden niet significant van elkaar (χ² = .31, df = 1, p = .58, φ = .02).

Gezien de gehanteerde categorieën (zie Tabel 6.39.) is het helaas niet geheel mogelijk de steekproef te vergelijken met de beroepsbevolking op de door het CBS gehanteerde tweedeling “westerse-” en “niet-westerse allochtoon”. Het CBS rekent namelijk Indonesië, Japan en Australië tot westerse allochtonen en mensen met een Aziatische achtergrond als niet-westerse allochtonen. In ons geval zitten personen echter bij elkaar in één groep waardoor deze niet uit elkaar te houden zijn. Wanneer de personen uit Azië gerekend werden tot niet-westerse allochtonen, bleek er nauwelijks verschil tussen het aantal niet-westerse allochtonen in de steekproef (8.6%) vergeleken met het aantal niet-westerse allochtonen in de totale beroepsbevolking (9.6%), hoewel dit verschil wel significant was (χ² = 17.42, df = 1, p = .00, φ = .07). Met deze indeling verschilde het aantal westerse allochtonen in de beroepsbevolking (10.6%) significant van het aantal westerse allochtonen in de steekproef (4.7%), hoewel het verschil ook weer relatief klein was (χ² = 108.65, df = 1, p = .00, φ = .16). Bij deze resultaten dient dus rekening gehouden te worden met de mogelijke invloed van het verschil in indeling wat betreft westers- en niet westerse allochtonen.

Ten opzichte van het aantal allochtonen bestond 64.5% uit niet-westerse allochtonen in de huidige steekproef, ten opzichte van 53.6% in de beroepsbevolking (2013). Deze aantallen verschilden significant van elkaar, maar opnieuw was de grootte van het effect relatief klein (χ² = 30.31, df = 1, p = .00, φ = .24).

De gemiddelde leeftijd van autochtonen was 45.0 (SD = 12.3), terwijl de gemiddelde leeftijd bij allochtonen 40.1 (SD = 12.8) was. Een ANOVA-toets wees uit dat autochtonen een significant hogere leeftijd hadden dan allochtonen in de steekproef (F(1,3991) = 60.96, p = .00); de effectgrootte Cohen’s d was .37 wat duidt op een gemiddeld effect. Het effect van leeftijd op scores op de ACT Algemene Intelligentie is echter klein (zie sectie 6.8.3.), waardoor de invloed hiervan op de resultaten gering zal zijn.

De indeling van autochtonen en allochtonen is weergegeven in Tabel 6.40.

Tabel 6.40. Verdeling opleidingsniveaus onder autochtonen en allochtonen in de steekproef.
	Autochtonen			Allochtonen			Totaal			Categorie
	Freq.	%	Freq.		%	Freq.		%
Lagere school/basisonderwijs	179	5.2	39		7.3	218		5.4	Laag
VMBO: basisberoepsgerichte leerweg (BB)	384	11.1	52		9.7	436		10.9	Laag
VMBO: kaderberoepsgerichte leerweg (KB)	175	5.0	27		5.0	202		5.0	Laag
VMBO: Gemengde leerweg (GL)	188	5.4	18		3.4	206		5.1	Laag
VMBO: Theoretische leerweg (TL)	228	6.6	23		4.3	251		6.3	Midden
HAVO	263	7.6	36		6.7	299		7.5	Midden
VWO	105	3.0	15		2.8	120		3.0	Hoog
MBO 1: Assistent beroepsbeoefenaar	101	2.9	16		3.0	117		2.9	Laag
MBO 2: Medewerker	294	8.5	61		11.4	355		8.9	Midden
MBO 3: Zelfstandig medewerker	332	9.6	39		7.3	371		9.3	Midden
MBO 4: Middenkaderfunctionaris	552	15.9	74		13.8	626		15.6	Midden
HBO: Oude stijl	224	6.4	38		7.1	262		6.5	Hoog
HBO: Bachelor	200	5.8	34		6.4	234		5.8	Hoog
HBO: Master	62	1.8	17		3.2	79		2.0	Hoog
WO: Bachelor	54	1.6	16		3.0	70		1.7	Hoog
WO: Master	66	1.9	23		4.3	89		2.2	Hoog
WO: Doctorandus	58	1.7	4		.7	62		1.5	Hoog
WO: Doctor	6	.2	3		.6	9		0.2	Hoog
Onbekend	3	.1	0		0.0	3		0.1
Totaal	3474	100	535		100	4009		100

 

Tabel 6.41. Verdeling autochtonen en allochtonen over de gegroepeerde opleidingsniveaus in de steekproef.
	Autochtonen		Allochtonen		Totaal
	Freq.	%	Freq.	%	Freq.	%
Laag	1027	29.6	152	28.4	1179	29.4
Midden	1669	48.0	233	43.6	1902	47.4
Hoog	775	22.3	150	28.0	925	23.1
Onbekend	3	0.1	0	0.0	3	0.1
Totaal	3474	100	535	100	4009	100

Om de groepen op basis van opleidingsniveau te kunnen vergelijken hebben we de opleidingsniveaus in drie categorieën ingedeeld, waarbij we de driedeling van het CBS gehanteerd hebben. Deze verdeling is weergegeven in Tabel 6.41. Een χ²-toets wees uit dat allochtonen en autochtonen van elkaar leken te verschillen wat betreft opleidingsniveau (χ² = 8.77, df = 2, p = .01). Echter, de effectgrootte Cramer’s V was .05, wat duidt op een zeer klein effect. Allochtonen en autochtonen waren dus goed vergelijkbaar wat betreft hun opleidingsniveau.

De θ’s en hun standaardafwijkingen van autochtonen en allochtonen op basis van de drie subtests en de g-score zijn weergegeven in Tabel 6.42.

Tabel 6.42. Verschillen in scores op de ACT Algemene Intelligentie, etniciteit – gemengde steekproef.
Test	Autochtoon					Allochtoon
	N	Gemiddelde	SD			N	Gemiddelde	SD		d
Cijferreeksen	2550	-.10	.93			421	-.31	.90		.24**
Figurenreeksen	2442	-.17	.85			385	-.20	.81		.04
Verbale Analogieën	2275	-.25	.93			378	-.47	.86		.25**
g-score	3474	-.17	.79			535	-.35	.76		.23**

**p < .01  (2-zijdig).

Gemengde steekproef

Een t-toets wees uit dat de θ’s op basis van de Figurenreeksentest niet significant van elkaar verschilden (t(2825) = 0.70, p = .49). Autochtonen scoorden echter wel significant hoger op de Cijferreeksentest dan allochtonen (t(2969) = 4.43, p = .000); hetzelfde gold voor de Verbale Analogieën (t(2651) = 4.33, p = .000). Ook de g-scores van allochtonen en autochtonen verschilden significant van elkaar (t(4007) = 4.93, p = .000). De effectgrootten d tonen aan dat het gaat om verschillen van kleine grootte (Cohen, 1988).

Wanneer we de verschillen in SD-eenheden uitdrukken zijn de verschillen maximaal ¼ SD: in de praktijk betekent dit dus dat het om een klein verschil zal gaan. In vergelijking met de waarden genoemd in sectie 6.8.4. zijn de gevonden verschillen in scores bij de ACT Algemene Intelligentie klein te noemen in vergelijking met eerdere bevindingen en andere tests. Gezien één van de doelen van de test – zo cultuurvrij mogelijk testen – is dit een belangrijke bevinding. Het is ook belangrijk om op te merken dat we helaas geen informatie hebben over bijvoorbeeld taalvaardigheid of verblijfsduur in Nederland (of van de ouders) van de respondenten: het is mogelijk dat wanneer gecontroleerd wordt voor deze factoren dat de verschillen tussen autochtonen en allochtonen nog lager uit zouden vallen.

Verschillen naar generatie

 Omdat uit de literatuur bekend is dat er de effecten van etniciteit verschillen bij eerste- en tweedegeneratieallochtonen hebben we ook gekeken naar de verschillen in scores tussen autochtonen enerzijds en allochtonen van de eerste en tweede generatie. De effectgrootten zijn weergegeven in Tabel 6.43.

Tabel 6.43. Effecten etniciteit voor eerste- en tweedegeneratieallochtonen.
	1e gen.	2e gen.
	d	d
Cijferreeksen	.29**	.20**
Figurenreeksen	.10	-.03
Verbale Analogieën	.39**	.12
g-score	.33**	.15*
*p <.05  (2-zijdig) . ** p < .01  (2-zijdig).N1e generatie = 153-220, N2e generatie = 208-288.

Geheel in overeenstemming met eerder onderzoek zien we dat de effecten bij tweedegeneratieallochtonen aanzienlijk kleiner zijn dan bij eerstegeneratieallochtonen. Opvallend is dat Figurenreeksen bij beide groepen geen significante verschillen met autochtonen laat zien, vermoedelijk door het cultuurvrije karakter van de test. Ook noemenswaardig is dat de effectgrootte bij eerste eerstegeneratieallochtonen het grootst is voor de verbale test (wat we op basis van verklaringen uit de literatuur ook verwachtten), terwijl dit effect bijna verdwenen is bij tweedegeneratieallochtonen. Dit is vermoedelijk het geval doordat zij in Nederland opgegroeid zijn en dus meer kennis van de taal hebben (Van den Berg, 2001; Van den Berg en Bleichrodt, 2000)). Tot slot is het gevonden effect bij de g-score bij tweedegeneratieallochtonen klein te noemen, en opvallend is ook dat deze score ongeveer gehalveerd is ten opzichte van het effect bij eerstegeneratieallochtonen.

Verschillen bij Turken, Marokkanen, Surinamers en Antillianen

 In Tabel 6.44. staan de effectgrootten van de verschillen tussen de ‘traditionele’ herkomstgroeperingen Turken, Marokkanen, Surinamers en Antillianen weergegeven. Opvallend is dat hier de effecten wat groter zijn. De oorzaak hiervan leek te verklaren te kunnen worden door het feit dat voor deze vier groepen de meerderheid ouders had die beiden in het buitenland waren geboren (73.9%). Het is aannemelijk dat de voertaal hierdoor thuis niet Nederlands geweest is, wat invloed gehad kan hebben op de scores. Het verschil in scores met autochtonen is wederom het kleinst voor de Figurenreeksentest. Over het algemeen zijn de gevonden verschillen overigens relatief aan de lage kant, in vergelijking met de eerdere genoemde onderzoeken.

Tabel 6.44. Effectgrootten voor traditionele herkomstgroepringen.
	d
Cijferreeksen	.43**
Figurenreeksen	.20*
Verbale Analogieën	.38**
g-score	.47**
*p <.05  (2-zijdig) . ** p < .01  (2-zijdig).N = 141-188

Steekproef uit Ixly database

Deze steekproef bestond voor 87.7% uit mannen, 5.3% uit vrouwen en voor 7.0% was het geslacht onbekend. Gezien het geringe aantal vrouwen is er niet gekeken of de twee groepen verschilden wat betreft het aantal mannen en vrouwen. De gemiddelde leeftijd was 32.6 jaar (SD = 10.3), variërend tussen de 18 en 61 jaar. Van 16 personen (5.6%) was de leeftijd onbekend. Allochtonen en autochtonen verschilden niet van elkaar wat betreft leeftijd (t(266) = .72, p = .47).

In Tabel 6.45. zijn de opleidingsniveaus weergegeven van beide groepen.

Tabel 6.45. Opleidingsniveau allochtonen en autochtonen in de Ixly steekproef.
	Autochtonen		Allochtonen		Categorie
	Freq.	%	Freq.	%
Lagere school/basisonderwijs	12	6.2	6	6.7	Laag
VMBO: basisberoepsgerichte leerweg (BB)	32	16.5	13	14.4	Laag
VMBO: kaderberoepsgerichte leerweg (KB)	10	5.2	5	5.6	Laag
VMBO: Gemengde leerweg (GL)	2	1.0	0	0.0	Laag
VMBO: Theoretische leerweg (TL)	9	4.6	6	6.7	Midden
HAVO	12	6.2	4	4.4	Midden
VWO	6	3.1	2	2.2	Hoog
MBO 1: Assistent beroepsbeoefenaar	11	5.7	6	6.7	Laag
MBO 2: Medewerker	39	20.1	22	24.4	Midden
MBO 3: Zelfstandig medewerker	27	13.9	9	10.0	Midden
MBO 4: Middenkaderfunctionaris	21	10.8	10	11.1	Midden
HBO: Oude stijl	6	3.1	3	3.3	Hoog
HBO: Bachelor	3	1.5	3	3.3	Hoog
HBO: Master	0	0.0	1	1.1	Hoog
WO: Doctorandus	1	.5	0	0.0	Hoog
Onbekend	3	1.5	0	0.0
Totaal	194	100	90	100

 De twee groepen verschilden niet van elkaar wat betreft opleidingsniveau (zie Tabel 6.46.) wat bleek uit een χ²-toets (χ² = .24, df = 2, p = .89).

Tabel 6.46. Gegroepeerd opleidingsniveau allochtonen en autochtonen in de Ixly steekproef.
	Autochtonen		Allochtonen		Totaal
	Freq.	%	Freq.	%	Freq.	%
Laag	67	34.5	30	33.3	97	34.2
Midden	108	55.7	51	56.7	159	56.0
Hoog	16	8.2	9	10.0	25	8.8
Onbekend	3	1.5	0	0.0	3	1.1
Totaal	194	100	90	100	284	100

De bevindingen bij de steekproef uit de Ixly database zijn weergeven in Tabel 6.47.

Tabel 6.47. Verschillen in scores op de ACT Algemene Intelligentie, etniciteit steekproef uit Ixly database.
Test	Autochtoon   (N = 194)			Allochtoon   (N = 90)
	Gemiddelde	SD		Gemiddelde	SD		d
Cijferreeksen	-.04	.74		-.22	.71		.25
Figurenreeksen	.13	.82		-.16	.70		.39**
Verbale Analogieën	.07	.66		-.26	.64		.51**
g-score	.04	.57		-.23	.51		.50**

** p < .01  (2-zijdig).

Tabel 6.47. laat een ander patroon zien dan Tabel 6.42. Een t-toets wees uit dat de θ’s op basis van de Cijferreeksentest niet significant van elkaar verschilden (t(282) = 1.95, p = .05). Interessant om op te merken is dat dit in eerder onderzoek ook gevonden werd (zie Van den Berg en Bleichrodt, 2000).

Autochtonen scoorden echter wel significant hoger op de Figurenreeksentest dan allochtonen (t(282) = 2.94, p = .004); hetzelfde gold voor de Verbale Analogieën (t(282) = 3.98, p = .000). Ook de g-scores van allochtonen en autochtonen verschilden significant van elkaar (t(282) = 3.86, p = .000). De effectgrootten d tonen aan dat het gaat om verschillen van gemiddelde grootte (Cohen, 1988).

Effectgrootten bij verschillende groepen allochtonen

In Tabel 6.48. staan de effectgrootten voor verschillende groepen allochtonen weergegeven. Een positieve effectgrootte betekent dat autochtonen hoger scoorden dan allochtonen.

Tabel 6.48. Effectgrootten voor verschillende groepen allochtonen.
	1e gen.	2e gen.	TMSA
	d	d	d
Cijferreeksen	.43*	.09	.27
Figurenreeksen	.48*	.32	.47**
Verbale Analogieën	.64**	.40*	.53**
g-score	.66**	.37*	.56**
Noot. TMSA = Turken, Marokkanen, Surinamers en Antillianen.   * p < .05 , ** p < .01  (2-zijdig). N1e generatie = 35, N2e generatie = 53, NTMSA= 58.

We zien grotendeels hetzelfde patroon als bij de totale steekproef. De effecten zijn over het algemeen groter bij eerstegeneratieallochtonen dan bij tweedegeneratieallochtonen, waarbij de verbale test een groter verschil tussen allochtonen en autochtonen vertoont. Interessant is dat de Turken, Marokkanen, Surinamers en Antillianen wat betreft effectgrootten ongeveer tussen de twee generaties in lijken te liggen. Dit lijkt verklaard te kunnen worden door het feit dat, hoewel iets meer dan de helft (63%) van deze personen van de 2^e generatie is, toch het overgrote deel hiervan (89%) beide ouders heeft die in het buitenland zijn geboren. Ook hier kunnen we overigens weer concluderen dat de gevonden effecten klein tot gemiddeld zijn en hiermee minder groot dan bij andere tests.

6.8.4.2. Conclusie verschillen tussen autochtonen en allochtonen

Het is niet eenvoudig om een eenduidige conclusie te trekken op basis van de beschreven resultaten, omdat de bevindingen bij de twee verschillende steekproeven enigszins van elkaar verschillen. Het voordeel van de gemengde steekproef is dat het hier gaat om een grote steekproef, waarbij het percentage allochtonen in de steekproef (13%) meer overeenkomt met het percentage allochtonen in de beroepsbevolking (19% in 2013). Het nadeel van de gemengde steekproef is dat dit deels uit personen bestaat (namelijk uit de kalibratiesteekproef) die de items niet adaptief gemaakt hebben. Het nadeel van de steekproef uit de Ixly database is dat deze verzameld is bij een zeer specifieke groep, waarbij het aantal allochtonen relatief groot was ten opzichte van de totale steekproef (32%).

Afgaande op de grootste steekproef lijkt het erop dat geen significante verschillen zijn tussen autochtonen en allochtonen in θ’s die gebaseerd zijn op de Figurenreeksentest, terwijl dit wel het geval was bij de andere tests. Dit vormt deels bewijs voor het feit dat de Figurenreeksen-subtest cultuurvrij meet en dat allochtone kandidaten niet benadeeld zullen zijn ten opzichte van autochtonen wanneer deze test afgenomen wordt. Aangezien het verschil bij de Ixly steekproef wat groter was (d = .39) moet deze conclusie echter nog niet als definitief beschouwd worden. Opvallend was dat bij de kandidaatssteekproef er geen significante verschillen werden gevonden tussen allochtonen en autochtonen in scores op de Cijferreeksentest, terwijl dit in de gemengde steekproef wel het geval was. De effectgrootten waren echter ongeveer hetzelfde (± d = .25) in beide steekproeven, wat duidt op een klein effect. Uitgesplitst naar verschillende groepen allochtonen kwamen de bevindingen bij de ACT Algemene Intelligentie grotendeels overeen met eerdere bevindingen uit de literatuur.

Er worden dus verschillen gevonden tussen allochtonen en autochtonen in scores op de ACT Algemene Intelligentie: echter, vrijwel voor elke ‘normale’ intelligentietest (dus niet specifiek ontworpen om culturele bias tegen te gaan) geldt dat allochtonen significant lager scoren dan autochtonen (voor een overzicht zie bijvoorbeeld Van den Berg en Bleichrodt, 2000). De ACT Algemene Intelligentie is dus niet de enige test waarbij dit het geval is. Sterker, voor alle gevonden verschillen gaat op dat ze qua grootte te kwalificeren als ‘klein’ of ‘gemiddeld’. Vergeleken met eerdere bevindingen (Van den Berg, 2001; Van den Berg en Bleichrodt, 2000; Te Nijenhuis et al., 2004) zijn deze verschillen dus relatief klein: dit maakt de ACT Algemene Intelligentie goed in te zetten is bij zowel allochtonen als autochtonen. Dit gezegd hebbende kunnen gebruikers wel eventueel rekening houden met de gevonden verschillen bij de interpretatie van de scores.

De hierboven gevonden verschillen lijken te indiceren op testniveau dat de Figurenreeksentest autochtonen niet duidelijk bevoordeeld ten opzichte van allochtonen. Op itemniveau kan er nog wel sprake van itembias zijn: dit is het geval als autochtonen op een andere manier reageren op items dan allochtonen. Om dit te onderzoeken wordt in de volgende sectie onderzoek besproken naar DIF (differential item functioning, zie bijvoorbeeld Zumbo, 1999): deze analyses toetsen de hypothese dat de scores op items tussen twee personen uit verschillende groepen niet significant van elkaar verschillen, wanneer de (latente) score op het construct dat dit item meet constant gehouden wordt.

6.9. Onderzoek naar Differential Item Functioning (DIF)

Zoals beschreven in Hoofdstuk 1 en Hoofdstuk 5 van deze handleiding was een doel bij de ontwikkeling van de ACT Algemene Intelligentie om de test zo cultureel rechtvaardig mogelijk te laten zijn. Cultureel rechtvaardig betekent dat geen onterechte vertekening (bias) ontstaat bij individuele uitkomsten en dat alleen reële verschillen tussen individuen zichtbaar worden in relatie tot de beroepspopulatie. Deze reële verschillen hebben immers betekenis voor de Nederlandse arbeidsmarkt.

 Itembias

In sectie 6.8.4. hebben we al de verschillen in scores tussen autochtonen en allochtonen, mannen en vrouwen en verschillen op basis van leeftijd besproken. Wat betreft de gevonden verschillen in gemiddelden tussen autochtonen en allochtonen bleek bijvoorbeeld dat – op subtest- en testniveau – deze  overeenkwamen met eerder gevonden verschillen in de literatuur, met de aantekening dat de verschillen relatief klein waren bij de ACT Algemene Intelligentie. Deze resultaten zeggen echter nog niets over eventuele itembias. Er is sprake van itembias als autochtonen op een andere manier reageren op een item of een item anders interpreteren dan allochtonen. Om dit te onderzoeken hebben we een aantal DIF (differential item functioning, zie bijvoorbeeld Zumbo, 1999) analyses uitgevoerd: deze analyses toetsen de hypothese dat de scores op items tussen twee personen uit verschillende groepen niet significant van elkaar verschillen, wanneer de (latente) score op het construct dat dit item meet constant gehouden wordt. Met andere woorden, twee persoon uit verschillende groepen (bijvoorbeeld een man en een vrouw) met hetzelfde intelligentieniveau moeten dezelfde kans hebben om een item goed te hebben. DIF kan op basis van allerlei achtergrondkenmerken optreden; daarom hebben we naast DIF-analyses op basis van etniciteit ook analyses gedaan op basis van leeftijd en geslacht.

6.9.1. DIF in adaptieve tests

6.9.1.1. Mantel-Haenszel (MH) procedure

 Een veelgebruikte methode voor de detectie van DIF is de Mantel-Haenszel (MH) odds ratio (Holland & Thayer, 1988; Mantel, 1963; Mantel & Haenszel, 1959). De MH procedure kan beschouwd worden als de ‘gouden standaard’ voor DIF detectie (Roussos & Stout, 1996; Jodoin & Gierl, 2001), omdat het een zeer sterke, unbiased detectiemaat is (Van der Linden & Glas, 2010). Deze procedure toetst de hypothese dat bij een gelijke score op de beoogde (latente) trek, de kans op het goed hebben van een item voor personen uit twee groepen gelijk is. Voor deze test zijn er drie zaken van belang; een itemscore, een groepsvariabele en een matchingscriterium. De itemscore is in ons geval simpelweg of iemand een vraag goed had (1, anders 0). De groepsvariabele duidt aan tot welke groep iemand behoort: hierbij is er één referentiegroep (in ons geval mannen, of autochtonen) en één focale groep (vrouwen of allochtonen). Het matchingscriterium is de (latente) trek, waarop de leden van de groep gelijk gezet worden om te kijken of er verschillen in itemresponses zijn.

Op basis van dit matchingscriterium wordt de totale onderzoeksgroep in k categorieën verdeeld. Vervolgens wordt voor elke categorie de volgende 2×2 kruistabel berekend:

Groep	Goed	Fout	Totaal
Referentie	N1R	N0R	N1R + N0R
Focaal	N1F	N0F	N1F + N0F
Totaal	N1R + N1F	N0R + N0F	N

Voor elke k tabellen wordt de volgende formule ingevuld:

Gesommeerd over k tabellen levert dit de MH odds ratio â_MH op. De Educational Testing Service (ETS) maakt al meer dan 25 jaar (Zieky, 1993; Zwick, 2012) gebruik van een classificatieschema, gebaseerd op de MH D-DIF waarde (Dorans & Holland, 1993), waarbij MH D-DIF = -2.35ln(â_MH). Dit schema geeft weer in welke mate er sprake is van DIF (Potenza & Dorans, 1995) en is gestoeld op het idee dat bij de detectie van DIF significantie alleen niet genoeg is. Het vinden van een significant resultaat is namelijk mede afhankelijk van de steekproefgrootte, de relatieve grootte van de focale- en referentiegroep en de scoreverdelingen van de items (Lei, Chen, & Yu, 2006).

Het classificatieschema bestaat uit drie categorieën, waarbij zowel de significantie van de MH D-DIF statistiek als de absolute grootte een rol speelt:

• categorie C – “matige” tot “sterke” DIF: wanneer de MH D-DIF waarde significant groter is dan 1 en wanneer de absolute waarde >1.5 is. Holland (2004) toonde aan dat aan de eerste voorwaarde voldaan wordt wanneer |MD D-DIF|-1/SE_{MH D-DIF} > 1.645, waarbij SE_{MH D-DIF} de standaardfout van de MH D-DIF statistiek is.
• categorie B – “klein” tot “matige” DIF: wanneer een item niet in categorie C geplaatst kan worden, en wanneer de MH D-DIF waarde significant groter is dan 0 (MD D-DIF/SE_{MH D-DIF} > 1.96) en wanneer de absolute waarde groter is dan 1.
• categorie A – “verwaarloosbare” DIF: wanneer een item niet in categorie C of B geplaatst kan worden

Categorie B en C kunnen ieder weer geclassificeerd worden als B-/B+ of C-/C+, afhankelijk van de richting (positief of negatief) van de MH D-DIF waarde. Een negatieve MH D-DIF waarde geeft aan dat de referentiegroep bevoordeeld is (de kans op een goed antwoord is groter voor de referentiegroep dan de focale groep bij een gelijk intelligentieniveau), terwijl een positieve waarde aanduidt dat de focale groep bevoordeeld is (de kans op een goed antwoord is groter voor de focale groep dan de referentiegroep bij een gelijk intelligentieniveau).

Bij de MH procedure wordt het matchtingscriterium normaliter gevormd door de somscore van alle items van de schaal, exclusief het betreffende item (restscore). Echter, in het geval van adaptieve tests is dit geen optie: iedere persoon krijgt immers een ander aantal items en bovendien zijn het andere items, waardoor een simpele som van het aantal goed voor iedereen een andere betekenis heeft. Een score van 5 van iemand die relatief makkelijkere items heeft gehad heeft een andere betekenis dan een score van 5 van iemand die relatief moeilijkere items gehad heeft. Om dit probleem te ondervangen zijn er verschillende varianten van de MH procedure ontwikkeld voor adaptieve tests (Van der Linden & Glas, 2010). In het huidige onderzoek hebben we gebruik gemaakt van de ZTW-methode (Van der Linden & Glas, 2010; Zwick, Thayer, & Wingersky, 1994a; 1994b; 1995). In deze methode wordt het matchingscriterium gevormd door de geschatte θ-waarde op basis van de verkregen itemresponses.

6.9.1.2. Logistische regressie (LR)

Omdat de statistische power van de verschillende methoden om DIF te detecteren verschillen, zeker bij relatief kleinere onderzoeksgroepen (zoals bij ons het geval is), wordt aangeraden om meerdere methoden van onderzoek te gebruiken (Wood, 2011). Daarom hebben we ook een tweede methode gebruikt om items met DIF op te sporen, namelijk met behulp van ordinale logistische regressie (Swaminathan & Rogers, 1990).

Bij DIF-detectie op basis van ordinale logistische regressie worden drie modellen met elkaar vergeleken (Swaminathan & Rogers, 1990; Zumbo, 1999):

Model 1: Eerst wordt een ordinale logistische regressie uitgevoerd met het item als de afhankelijke variabele en de totaalscore op het construct dat door dit item gemeten wordt als onafhankelijke variabele.

Model 2: Vervolgens wordt de groepsvariabele als onafhankelijke variabele ingevoerd (bijvoorbeeld autochtoon/allochtoon).

Model 3: Vervolgens wordt de interactie tussen de totaalscore en de groepsvariabele als onafhankelijke variabele ingevoerd.

Bij adaptieve tests wordt de bovenstaande ‘totaalscore’ vervangen door de geschatte θ-waarde op basis van de verkregen itemresponses.

Een groot voordeel van de hiërarchische werkwijze is dat de mate van uniforme (Model 2 vs. Model 1) en non-uniforme DIF (Model 3 vs. Model 2) van elkaar kunnen worden onderscheiden (Zumbo, 1999).[13] De MH procedure zoals hierboven beschreven kan alleen uniforme DIF detecteren. Er is sprake van uniforme DIF als bijvoorbeeld de focale groep (bijvoorbeeld  allochtonen) altijd een lagere kans heeft het goede antwoord te kiezen op een bepaald item dan de referentiegroep (autochtonen), ongeacht de score van de persoon op het construct dat dit item meet. In dit geval is de allochtone kandidaat dus ‘benadeeld’: bij een gelijk intelligentieniveau heeft de allochtone kandidaat een lagere kans om het item goed te hebben dan de autochtone kandidaat. Echter, bij een gelijke intelligentiescore zouden allochtonen en autochtonen theoretisch dezelfde kans moeten hebben om het item goed te hebben. Is dit niet het geval, dan is dit item wellicht niet een equivalente maat voor het construct intelligentie, maar meet het misschien ook nog een ander construct (bijvoorbeeld Leesvaardigheid), waar de groepen op verschillen.

In termen van de itemresponstheorie betekent uniforme DIF dat de a-parameter niet verschilt tussen de twee groepen, maar alleen de b-parameter. Een voorbeeld hiervan is weergegeven in Figuur 6.9. De lijnen van de twee groepen lopen parallel, wat betekent dat de a-parameters voor beide groepen gelijk zijn. Echter, de moeilijkheid van het item lijkt te verschillen bij de twee groepen: bij een gemiddelde intelligentie (θ = 0) is de kans op een goed antwoord voor iemand uit de focale groep groter dan voor iemand uit de referentiegroep. Er is sprake van uniforme DIF omdat de kans op een goed antwoord altijd groter is voor leden uit de focale groep dan voor leden uit de referentiegroep, ongeacht iemands θ-score.

Figuur 6.9. Voorbeeld van item dat substantiële uniforme DIF vertoont.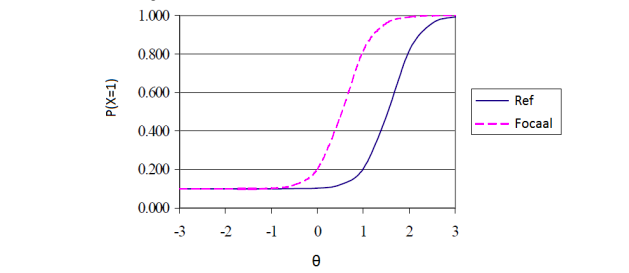

Bron: Zumbo (1999), p. 20

Bij non-uniforme DIF varieert het ‘bevoordeeld’ of ‘benadeeld’ zijn met de score van de persoon op het construct dat het item meet. Er is bijvoorbeeld sprake van non-uniforme DIF als bij een lage intelligentiescore de kans groter is dat een allochtone kandidaat (in vergelijking met een autochtone kandidaat met dezelfde score) het item goed heeft, terwijl bij een hoge intelligentiescore de kans kleiner is dat een allochtone kandidaat (in vergelijking met een autochtone kandidaat met dezelfde score) het item goed heeft.

Een voorbeeld hiervan is gegeven in Figuur 6.10. Bij beneden gemiddelde scores is de kans op een goed antwoord voor leden uit de focale groep groter dan voor leden uit de referentiegroep. Bij boven gemiddelde scores is precies het omgekeerde het geval. In IRT-termen betekent dit dat zowel de a- als b-parameter significant verschillen tussen de twee groepen (Steinberg, Thissen, & Wainer, 1990).

Figuur 6.10. Voorbeeld van item dat non-uniforme DIF vertoont.

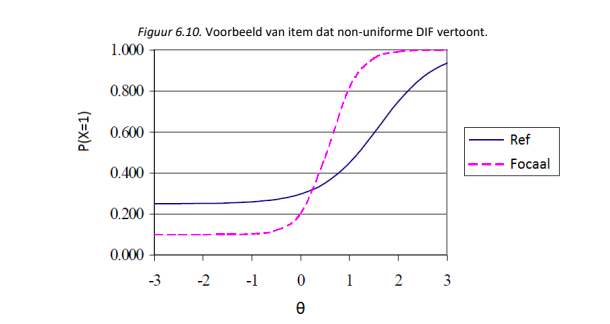
Bron: Zumbo (1999), p. 21

We kunnen spreken van substantiële DIF als er aan twee voorwaarden wordt voldaan. De eerste voorwaarde is gebaseerd op significantie: de fit van de modellen worden aan de hand van hun χ²-waarden vergeleken. Als de p-waarde van het verschil in χ²-waarden van Model 3 en Model 1 (met 2 vrijheidsgraden) kleiner is dan .05[14], dan is Model 3 dus significant beter dan Model 1 en kan er sprake zijn van DIF (Swaminathan & Rogers, 1990; Zumbo, 1999).

In het voorgaande wordt steeds gesproken dat er ‘sprake kan zijn van DIF’: onder invloed van bijvoorbeeld de steekproefgrootte, relatieve grootte van de focale- en referentiegroep en de moeilijkheid van de items kan de χ²-waarde significant worden (Lei et al., 2006; Swaminathan & Rogers, 1990; Zumbo, 1999). De tweede voorwaarde is daarom dat er aanzienlijke effectgrootten moeten zijn voordat er sprake kan zijn van substantiële DIF (Kirk, 1996; Zumbo, 1999; Zumbo & Hubley, 1998). Hiervoor wordt het verschil in verklaarde variantie, ΔR², tussen de verschillende modellen gebruikt. Zumbo en Thomas (1997) geven als richtlijn dat een ΔR² van tussen de 0 en .13 duidt op verwaarloosbare DIF, tussen de .13 en .26 op matige DIF en >.26 op sterke DIF. Jodoin en Gierl (2001) hanteren de categorieën: 0 – .035 als verwaarloosbaar, .035 – .07 als matig en >.07 als sterk. In het huidige onderzoek hanteren we deze laatste, strengere vuistregel. Alleen wanneer aan de beide voorwaarden (significantie en een substantiële effectgrootte) voldaan wordt dan kunnen we spreken van substantiële DIF.

Bovenstaande test met 2 vrijheidsgraden kan gezien worden als een omnibus test voor zowel uniforme als non-uniforme DIF. Een manier om vervolgens inzicht te krijgen in de mate van uniforme- en non-uniforme DIF is door de R²-waarden van Model 2 en Model 3 te vergelijken. Het verschil in R²-waarden tussen Model 1 en Model 3 is namelijk additief (bijvoorbeeld ΔR²_M3-M1 = .10): de ΔR² tussen Model 1 en Model 2 is representatief voor uniforme DIF (bijvoorbeeld ΔR²_M2-M1 = .08), de ΔR² tussen Model 3 en Model 2 is representatief voor non-uniforme DIF (bijvoorbeeld R²_M3-M2 = .02).

6.9.2. Differential Test Functioning (DTF)

Bij DIF wordt er op itemniveau gekeken of de kans op een goed antwoord verschilt tussen twee of meerdere groepen bij een gelijk intelligentieniveau. Er kan echter ook gekeken worden of zulke verschillen aggregeren tot bias op testniveau, dit wordt differential test functioning (DTF) genoemd. Gevonden DIF effecten hoeven niet per definitie tot DTF te leiden: wanneer DIF niet duidelijk in het voordeel (of nadeel) van één groep is dan kan op testniveau de DTF te verwaarlozen zijn. Andersom geldt dat er ook sprake kan zijn van substantiële DTF terwijl er weinig sprake lijkt te zijn van DIF: kleine en/of niet-significante effecten op itemniveau kunnen optellen tot substantiële bias op testniveau.

Daarom zijn er methoden ontwikkeld om DTF van een test te analyseren. De meest gebruikte methode is het vergelijken van de verwachte score op testniveau tussen groepen: de verwachte score is dan simpelweg de som van alle kansen (op een goed antwoord) op de losse items van een test. Bij adaptieve tests is dit echter complex: verschillende personen krijgen verschillende (aantallen) items waardoor een verwachte score niet eenvoudig te interpreteren is en te vergelijken is tussen groepen.[15]

De MH procedure levert een DTF-statistiek op die niet gebaseerd is op verwachte scores maar op de variantie van de DIF-statistieken in een test of itembank. Deze variantie, τ², kan gebruikt worden om de mate van DTF te kwalificeren. Penfield en Algina (2006) hanteren als vuistregel:

• τ² < .07 kleine mate van DTF (ongeveer maximaal 10% van de items hebben een absolute MH D-DIF waarde van 1)
• .07 < τ² < .14 gemiddelde mate van DTF
• > .14 sterke mate van DTF (ongeveer 25% van de items of meer hebben een MH D-DIF waarde van 1)

Om de gebruiker nog meer inzicht te geven in de mate van DTF hebben we voor iedere persoon de totale verwachte score berekend door voor iedere persoon voor elk getoonde item de “kans op een goed antwoord” te berekenen bij de geschatte θ voor deze persoon, en deze kansen op te tellen. Vervolgens is deze som gedeeld door het totaal aantal items dat iemand gemaakt heeft: omdat verschillende mensen een verschillend aantal items hebben gemaakt is er op deze manier voor gezorgd dat iedereen een totale verwachte score tussen de 0 en 1 kreeg. Deze kansen zijn vervolgens afgerond om ervoor te zorgen dat iedere persoon een score 0 of 1 kreeg. Deze dichotome variabele kon vervolgens als afhankelijke variabele gebruikt worden in logistische regressiemodellen, analoog aan de DIF analyses zoals hierboven beschreven. Bovendien geven we grafisch de voorspelde scores weer op basis van het logistische regressiemodel (analoog aan itemresponsfuncties, zie Hoofdstuk 1) om een beeld te krijgen van verschillen tussen groepen.[16]

6.9.3. Huidig onderzoek

Door het groot aantal missende waarden inherent aan het adaptieve karakter van de test hebben we alle analyses gedaan op zo groot mogelijke steekproeven, dus op de totale steekproef, en niet op e kandidaatssteekproef. Bij analyses op de kandidaatssteekproef waren er vaak te weinig observaties per item (of per item per groep) om DIF te kunnen detecteren. Meer informatie over de achtergrondkenmerken en de representativiteit van de steekproef is te vinden in sectie 6.8.

Voor de MH procedure is gebruik gemaakt van het programma DIFAS 5.0 (Penfield, 2005). Voor het matchingscriterium is de θ-score per subtest ingedeeld in 12 categorieën door de θ-schaal op te knippen in gelijke delen van .20 (-3 tot -2.8, -2.8 tot -2.6, … et cetera, 2.8 tot 3). Indelingen in meer categorieën leverden te veel lege cellen op of cellen met te kleine aantallen op in de 2×2 tabellen in de MH procedure: andere indelingen zijn wel geanalyseerd maar lieten vergelijkbare resultaten zien. Zwick en collegae (Zwick et al., 1994a; 1994b; 1995) stelden voor om als matchingscriterium niet de geschatte θ-score te gebruiken maar de verwachte score over de gehele itembank te hanteren. Deze verwachte score is te verkrijgen door voor de geschatte θ de kans op ieder item te berekenen en deze kansen vervolgens te sommeren over de gehele itembank. Alle analyses uit de MH procedure zijn ook gedaan met dit matchingscriterium maar leverden geen andere resultaten op; daarom zijn deze resultaten hier niet weergegeven.

De MH procedure bleek minder items als potentiële DIF-items te markeren dan de LR methode. Daarom hebben we bij de classificatie van de items in de ETS categorieën ook items ingedeeld die significante DIF leken te vertonen op basis van de LR methode. Omdat de MH procedure uniforme DIF toetst, hebben we hierbij gekeken naar het verschil in χ²-waarden tussen Model 2 en Model 1 (met 1 vrijheidsgraad).

Voor de logistische regressieprocedure is gebruik gemaakt van het difR pakket (Magis, Beland, Tuerlinckx, & De Boeck, 2010) in R (R Core Team, 2016). Voor DIF op basis van leeftijd hebben we alleen gebruik gemaakt van de LR methode omdat bij de MH procedure slechts twee groepen vergeleken kunnen worden. Bij de LR methode kan ook een continue of discrete variabele (zoals leeftijd) als groepsvariabele gebruikt worden.

Er zijn ook DIF-detectie methoden op basis van IRT: hierin worden de a– en b-parameters geschat voor de verschillende groepen om vervolgens te onderzoeken of deze significant van elkaar verschillen (met behulp van een likelihood ratio test (LRT); Thissen, Steinberg, & Wainer, 1988; Steinberg et al., 1990). Het probleem bij deze methode is dat voor een stabiele schatting van de itemparameters grote steekproeven nodig zijn (de parameters worden immers per subgroep geschat); in ons geval was deze methode om deze reden minder geschikt. Desalniettemin hebben we met behulp van het programma IRTLRTDIF (Thissen, 2001) de items onderzocht op DIF: de resultaten waren echter vrijwel gelijk aan de resultaten van de LR methode. Daarom zijn alleen de resultaten van de LR methode weergegeven. De instabiliteit van de itemparameters in de IRTLRTDIF methode bleek uit enkele zeer grote a-waarden of zeer grote negatieve of positieve b-waarden.

6.9.4. Resultaten

6.9.4.1. Etniciteit

In Tabel 6.49. zijn het aantal en het percentage items dat op basis van de MH D-DIF of LR waarden significante uniforme DIF leek te vertonen op basis van etniciteit, en de classificering van items in de ETS categorieën weergegeven.

Tabel 6.49. Resultaten DIF analyses op basis van etniciteit (allochtoon/autochtoon).
						ETS classificatie
		MH	LR	Totaal		C-	B-	A	B	C+
Cijferreeksen	Aantal	10	13	14		2	4	197	7	1
	%	5	6	7		1	2	93	3	0
Figurenreeksen	Aantal	7	5	8		0	6	179	1	1
	%	4	3	5		0	3	96	1	1
Verbale Analogieën	Aantal	14	17	19		1	9	192	8	1
	%	7	8	9		0	4	91	4	0
A = klein, B = matig, C = sterk

Uit Tabel 6.49. blijkt dat slechts een klein aantal items DIF lijkt te vertonen op basis van etniciteit, en dat dit geldt voor alle drie de subtests. Bovendien blijkt uit het rechterpaneel dat de mate van DIF klein is: Cijferreeksen,  Figurenreeksen en Verbale Analogieën hebben respectievelijk slechts 3 (1%), 1 (1%) en 2 (0%) items uit de C-categorie. Cijferreeksen, Figurenreeksen en Verbale Analogieën hebben respectievelijk 11 items (5%), 7 (4%) en 17 (8%) uit categorie B. Voor Figurenreeksen vinden we de minste verschillen; dit was ook te verwachten gezien het feit dat dit type item het meest cultuurvrij is (zie Hoofdstuk 1 en 6). Opvallend is verder dat Verbale Analogieën de meeste DIF-items heeft; gezien de verbale component van de items zijn er meer DIF-effecten tussen autochtonen en allochtonen te verwachten dan bij de andere subtests (Schmitt & Dorans, 1990; Te Nijenhuis, 1997; Van den Berg, 2001). Er zijn echter evenveel B- als B+ items, wat betekent dat allochtonen niet duidelijk ‘benadeeld’ lijken te zijn. Dit geldt over het algemeen voor alle drie de subtests.

Een vergelijkbaar beeld kwam naar voren uit de DTF analyses: de τ²-waarden voor Cijferreeksen, Figurenreeksen en Verbale Analogieën waren respectievelijk .034, .014, en .055. Alle drie de waarden waren <.07, wat erop duidt dat we mogen verwachten dat er op itembankniveau nauwelijks sprake van bias zal zijn op basis van etniciteit.

In Tabel 6.50. zijn de resultaten weergegeven van de LR methode. Opvallend is weer dat Figurenreeksen, zoals verwacht, de minste items had waar sprake leek te zijn van DIF. Er bleken niet veel verschillen te zitten tussen het aantal items gemarkeerd als uniforme DIF en non-uniforme DIF. De effectgrootten (twee rechter kolommen Tabel 6.50.) toonden aan dat de items die op basis van hun significantie gemarkeerd waren als ‘potentiële DIF-items’ geen noemenswaardige mate van DIF vertoonden. Hoewel weinig relevant bij kleine effectgrootten lieten de R²-waarden zien dat bij Cijferreeksen en Figurenreeksen er voornamelijk non-uniforme DIF items waren, terwijl bij Verbale Analogieën er evenveel items uniforme en non-uniforme DIF vertoonden. Inhoudelijke inspectie van de potentiële DIF-items liet verder zien dat er geen duidelijk patroon te herkennen was in de items die DIF leken te vertonen.

Tabel 6.50. Resultaten DIF analyses op basis van etniciteit (allochtoon/autochtoon) – LR methode
		Sig		Gemiddelde   ΔR2 M3-M1	Max.   ΔR2
Cijferreeksen	Aantal	21		.0257	.0429
	%	10
Figurenreeksen	Aantal	8		.0248	.0372
	%	4
Verbale Analogieën	Aantal	18		.0243	.0353
	%	8

In Figuur 6.11. zijn de resultaten weergegeven van de DTF analyses op basis van logistische regressie. Op basis van de figuren lijkt er enig verschil te zitten tussen de verwachte score van autochtone- en allochtone kandidaten op basis van hun θ-scores. Opvallend is dat allochtonen bevoordeeld lijken te worden, maar dat bij hogere θ-waarden autochtonen iets bevoordeeld worden (non-uniforme DTF). Formele χ²-toetsen wezen uit dat alleen voor Figurenreeksen (χ²(2) = 10.9, p = .00) en Verbale Analogieën (χ²(2) = 20.4, p = .00) een indicatie voor DIF op testniveau was (Cijferreeksen; χ²(2) = 6.0, p = .05). Echter, het vinden van significante effecten leek vooral door de grotere steekproef te komen; de ΔR² waren respectievelijk .0013, .0028 en .0000 voor Cijferreeksen, Figurenreeksen en Verbale Analogieën. Op testniveau lijkt er dus weinig tot geen sprake van bias op basis van etniciteit.

Gezien het feit dat allochtonen niet duidelijk benadeeld lijken te zijn, dat er weinig tot geen items substantiële DIF leken te vertonen en dat deze kleine verschillen op test- of itembankniveau nauwelijks tot verschillen leiden hebben we besloten geen items op basis van de DIF analyses uit de itembanken te verwijderen.

Figuur 6.11. Verwachte scores op basis van DTF analyses – etniciteit.

 

6.9.4.2. Geslacht

 In Tabel 6.51. zijn het aantal en het percentage items dat op basis van de MH D-DIF of LR waarden significante uniforme DIF leek te vertonen op basis van geslacht, en de classificering van items in de ETS categorieën weergegeven.

Tabel 6.51. Resultaten DIF analyses op basis van geslacht (man/vrouw).
						ETS classificatie
		MH	LR	Totaal		C-	B-	A	B	C+
Cijferreeksen	Aantal	15	20	18		2	9	193	6	1
	%	7	9	8		1	4	91	3	0
Figurenreeksen	Aantal	11	10	13		0	7	174	6	0
	%	6	5	7		0	4	93	3	0
Verbale Analogieën	Aantal	13	22	22		0	8	191	14	0
	%	6	10	11		0	4	90	7	0
A = klein, B = matig, C = sterk

Tabel 6.51. laat zien dat in elk van de drie subtests ongeveer 10% van de items DIF op basis van geslacht vertoont. Uit het rechterpaneel blijkt de mate van DIF echter klein: alleen Cijferreeksen heeft items uit de C-categorie, maar dit zijn er slechts 3 (1%). Cijferreeksen, Figurenreeksen en Verbale Analogieën hebben respectievelijk 15 items (7%), 13 (7%) en 22 (11%) uit categorie B. Verder zien we dat mannen of vrouwen niet duidelijk bevoordeeld of benadeeld worden: er bevinden zich ongeveer evenveel items in de – en + categorieën. Dit kwam ook naar voren uit de DTF-analyses:  de τ²-waarden voor Cijferreeksen, Figurenreeksen en Verbale Analogieën waren respectievelijk .039, .016 en .021. Op itembank- of testniveau leek er dus geen sprake van vertekeningen te zijn op basis van geslacht.

Op basis van de LR methode kunnen we dezelfde conclusies trekken (Tabel 6.52.). Ongeveer 10% van de items in elk van de subtests vertoont (uniforme/non-uniforme) DIF. Bij Verbale Analogieën lijkt er voornamelijk sprake te zijn van uniforme DIF. De effectgrootten toonden ook bij geslacht aan dat er over het algemeen sprake was van verwaarloosbare DIF. Inspectie van de R²-waarden van de verschillende modellen wees uit dat bij Cijferreeksen en Figurenreeksen evenveel sprake was van uniforme als non-uniforme DIF, terwijl er bij Verbale Analogieën voornamelijk sprake was van uniforme DIF (waarbij vrouwen voornamelijk bevoordeeld waren).

Bij zowel Cijferreeksen als Verbale Analogieën was er echter 1 item dat substantiële DIF vertoonde ΔR²_M3-M2 > .07, zie rechterkolom). Het bleek hier echter te gaan om items die nog niet vertoond waren aan kandidaten, maar alleen door mensen gemaakt waren in het kalibratieonderzoek. Het item van Cijferreeksen was op basis van andere item-fit statistieken bij de herkalibratie in juli 2016 al uit de itembank verwijderd. Om meer data te verzamelen in daadwerkelijke selectiesituaties hebben we besloten om het item van Verbale Analogieën in de itembank te behouden.

Tabel 6.52. Resultaten DIF analyses op basis van geslacht (man/vrouw) – LR methode
		Sig.		Gemiddelde   ΔR2 M3-M1	Max.   ΔR2
Cijferreeksen	Aantal	22		.0270	.1182
	%	10
Figurenreeksen	Aantal	15		.0181	.0417
	%	8
Verbale Analogieën	Aantal	20		.0256	.1135
	%	9

In Figuur 6.12. staan de resultaten van de logistische DTF analyses weergegeven voor geslacht.

Figuur 6.12. Verwachte scores op basis van DTF analyses – geslacht.

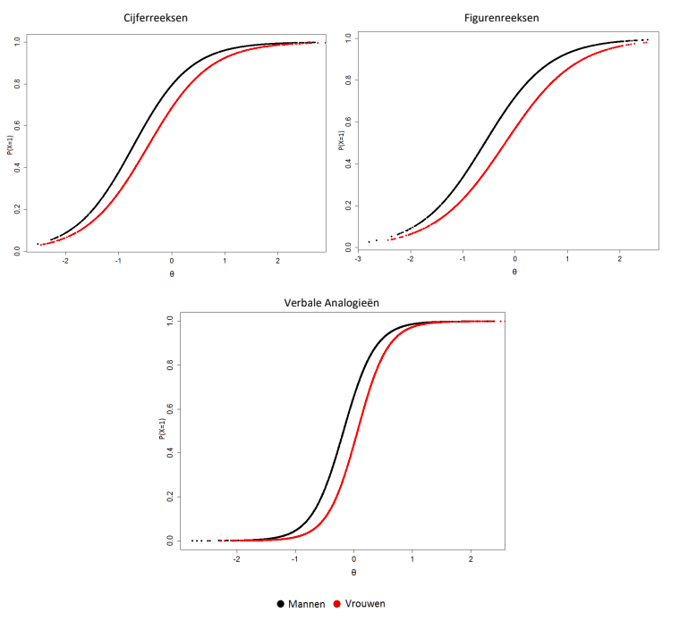
Op basis van een visuele inspectie van de voorspelde kansen voor mannen en vrouwen lijkt de afstand tussen de twee lijnen te duiden op uniforme DTF: vrouwen zijn in vergelijking met mannen benadeeld, en bij Figurenreeksen lijkt de bias het grootst. Hoewel de χ²-toetsen in eerste instantie weer op DTF leken te wijzen, duidden de R²-waarden weer op zeer kleine effecten (.0000, .0140, .0000). Ook hier lijkt er dus op testniveau weinig sprake van bias op basis van geslacht.

Bovenstaande resultaten hebben er toe geleid dat we ook op basis van de DIF analyses voor geslacht geen items uit de itembank hebben verwijderd.

6.9.4.3. Leeftijd

 In Tabel 6.53. zijn de resultaten weergegeven van de DIF analyses op basis van leeftijd. Er werden meer items als potentiële DIF items gemarkeerd dan bij de analyses op basis van etniciteit en geslacht. De gemiddelde effectgrootten zijn volgens de indeling van Jodoin en Gierl (2001) echter als klein te kwalificeren. In totaal waren er 5 items (2%) met een gemiddelde mate van DIF bij Verbale Analogieën, 8 items (4%) bij Cijferreeksen en 2 items (1%) bij Figurenreeksen.

Tabel 6.53. Resultaten DIF analyses op basis van leeftijd – LR methode
		Sig.		Gemiddelde   ΔR2 M3-M1	Max.   ΔR2
Cijferreeksen	Aantal	39		.0245	.0673
	%	18
Figurenreeksen	Aantal	20		.0188	.0381
	%	11
Verbale Analogieën	Aantal	36		.0235	.0585
	%	17

Inspectie van de R²-waarden toonde bij Cijferreeksen aan dat er iets meer items waren die voornamelijk uniforme DIF vertoonden dan die non-uniforme DIF vertoonden. Bij de uniforme DIF-items waren ouderen voornamelijk in het nadeel. Voor de non-uniforme items gold dat er ouderen of jongeren niet duidelijk in het voordeel waren.

Bij Figurenreeksen vertoonden meer items uniforme DIF dan non-uniforme DIF, waarbij ouderen ongeveer even vaak benadeeld werden als jongeren. Van de items die non-uniforme DIF vertoonden gold dat bij de meeste items ouderen met een hoge abstracte intelligentie en jongeren met een lage abstracte intelligentie bevoordeeld waren.

Bij Verbale Analogieën vertoonden de meeste items uniforme DIF, waarbij voor deze uniforme DIF-items gold dat ouderen ongeveer even vaak benadeeld werden als jongeren. Voor de non-uniforme items gold dat net als bij Figurenreeksen ouderen (of jongeren) niet duidelijk in het voordeel waren.

In Figuur 6.13. staan de resultaten van de logistische DTF analyses weergegeven voor leeftijd; puur voor de visuele weergave zijn de voorspelde waarden gepresenteerd voor de leeftijdsgroepen ‘tot 25’, ’25 tot 45’ en ‘>45’, in de analyses is leeftijd als continue variabele meegenomen.

Uit Figuur 6.11. blijkt dat er nauwelijks verschillen lijken te zijn in verwachte scores op basis van leeftijd. Dit bleek ook uit de logistische regressie (χ²(2) = 3.8, p = .15). Bij Figurenreeksen lijken vooral ouderen met een lager abstract intelligentieniveau benadeeld te worden ten opzichte van de jongste categorie. Dit verschil is bij hogere niveaus verdwenen. De middelste leeftijdscategorie lijkt over het algemeen bevoordeeld ten opzichte van de andere twee groepen. Hoewel er sprake leek van DTF op basis van het significantieniveau (χ²(2) = 19.4, p = .00), was de effectgrootte te verwaarlozen (ΔR²_M3-M1 = .0035). Bij Verbale Analogieën blijkt uit de figuur dat de middelste en jongste categorie nauwelijks van elkaar lijken te verschillen wat betreft verwachte scores, terwijl ouderen over de gehele θ-schaal benadeeld lijken te worden. De verschillen bleek echter verwaarloosbaar (χ²(2) = 24.5, p = .00, ΔR²_M3-M1 = .0000). Op basis van deze analyses blijkt dat we op testniveau dus weinig bias op basis van leeftijd mogen verwachten.

Figuur 6.13. Verwachte scores op basis van DTF analyses – leeftijd.

 

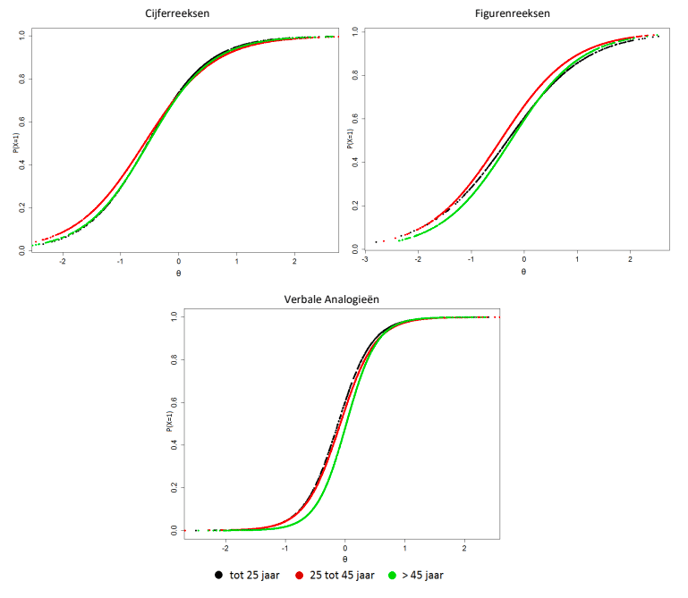
6.9.5. Conclusies ten aanzien van DIF bij de ACT Algemene Intelligentie

 Op basis van verschillende methoden – waarbij relatief strenge criteria werden gehanteerd –  is in dit onderzoek aangetoond dat er bij de ACT Algemene Intelligentie geen substantiële DIF verwacht kan worden op basis van etniciteit, geslacht en leeftijd. Er waren wel indicaties voor potentiële DIF bij een aantal items, maar de effectgrootten duidden op kleine verschillen tussen groepen. Bovendien bleken groepen niet consequent benadeeld of bevoordeeld: DTF analyses op test- en itembankniveau wezen dan ook uit dat we op testniveau weinig bias mogen verwachten op basis van etniciteit, leeftijd en geslacht.

6.10. Onderzoek naar person fit

6.10.1. Introductie

 In de secties over item-fit hebben we feitelijk gekeken of de items, en hun geschatte parameters, zich gedragen volgens het gestelde IRT-model. Op vergelijkbare wijze kan er gekeken worden naar person fit: bij person fit gaat het erom of personen antwoordpatronen laten zien die consistent zijn met het IRT-model. Op basis van een IRT-model kan het antwoordpatroon van een kandidaat voorspeld worden. Aan de hand van person fit-statistieken kunnen onwaarschijnlijke of inconsistente antwoordpatronen geïdentificeerd worden. Een inconsistent antwoordpatroon zou bijvoorbeeld zijn dat iemand alle makkelijkere vragen fout beantwoord heeft en alle moeilijkere vragen goed. Person fit is belangrijk voor de validiteit van de verkregen testscores: op basis van het antwoordpatroon van de testnemer wordt θ bepaald (sectie 1.4.2.), en aangezien er belangrijke beslissingen afhangen van deze schatting van θ (bijvoorbeeld een baan krijgen of niet) is het van belang zeker te zijn dat het antwoordpatroon op de ‘juiste’ manier tot stand is gekomen. De person fit zegt dus direct iets over de validiteit van de verkregen testscores op individueel niveau. Met andere woorden, als de person fit-statistieken aangeven dat een antwoordpatroon afwijkend is, dan kunnen we de juistheid van de uitkomsten van de test in twijfel trekken.

6.10.2. Person fit in adaptieve tests

Er zijn verschillende maten in de literatuur bekend die afwijkende scorepatronen kunnen detecteren; iedere maat kent vanzelfsprekend zijn eigen voor- en nadelen. Daarom hebben we ervoor gekozen twee maten te gebruiken. Namelijk de CUSUM-procedure en het aantal Guttman fouten.

6.10.2.1. CUSUM

In een adaptieve test kunnen personen met dezelfde geschatte θ daar op verschillende manieren komen, op basis van andere antwoordpatronen. Hier kunnen verschillende oorzaken voor zijn, bijvoorbeeld onachtzaamheid of gokgedrag. Bijvoorbeeld: de ene persoon kan eerst een aantal vragen fout hebben (door onachtzaamheid) en daarna er weer een aantal goed hebben, terwijl een andere persoon er bijvoorbeeld (meer conform het model) één goed heeft, dan weer één fout et cetera, en op dezelfde θ uitkomen. Een person fit-maat die hier goed inzicht in geeft is de “cumulative sum” procedure (CUSUM; Van Krimpen-Stoop & Meijer, 2002). Hoewel er veel person fit-statistieken bestaan in de literatuur, hebben wij daarom voor de CUSUM methode gekozen om de person fit van de ACT Algemene Intelligentie te onderzoeken.

De CUSUM procedure werkt als volgt. Op basis van de geschatte θ na het afronden van de ACT Algemene Intelligentie is voor elk item te berekenen wat de kans is op een goed antwoord (P): dit is de verwachte score (E). Voor elke geobserveerde score (O) kan dus het residu berekend worden (O – E). Op basis hiervan kan de statistiek T berekend worden: dit is simpelweg het residu gedeeld door het totaal aantal gemaakte items.

Vervolgens wordt deze score T en de residuen gebruikt om twee reeksen te creëren, één met positieve residuen, en één met negatieve residuen. De reeks met positieve residuen heeft een minimum van 0, de reeks met negatieve residuen een maximum van 0 (zie Figuur 6.14. en 6.15.).

Figuur 6.14. Formules van de CUSUM procedure.

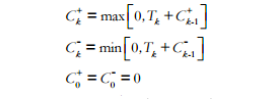
Bron: Egberink (2010, p. 56)

Figuur 6.15. Voorbeeld CUSUM procedure

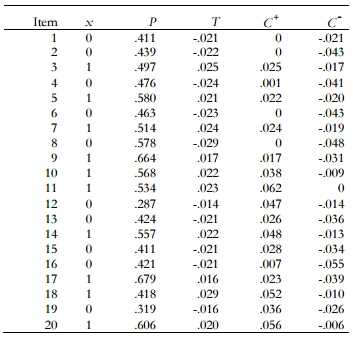
Bron: Egberink (2010, p. 57)

Deze persoon heeft 20 items gemaakt, waarbij het eerste item fout beantwoord is (O = 0), terwijl de verwachte score (E = ) .411 was. T is dus bij het eerste item (0 – .411) / 20 = -.021. Dit residu wordt van de C^– reeks afgetrokken; niet van de C⁺ reeks, omdat het minimum van deze reeks 0 is. Het zelfde principe wordt zo voor elk item herhaald. Uit dit voorbeeld wordt duidelijk dat C^– alleen een groot negatief geval wordt wanneer er consequent lager gescoord wordt dan voorspeld, en C⁺ alleen een groot positief geval als er hoger gescoord wordt dan voorspeld. Iemand die onachtzaam een test invult zal bijvoorbeeld relatief lagere C^–-waarden hebben, terwijl iemand die de antwoorden van een test heeft weten te bemachtigen relatief hogere C⁺-waarden zal hebben. De CUSUM procedure brengt dus mooi in kaart of mensen ‘te hoog’ of ‘te laag’ op een item scoren.

Voor iedere persoon die de ACT gemaakt heeft, hebben we bovenstaande reeksen berekend. Echter, dan moeten er nog aftestgrenzen voor C^– en C⁺ bepaald worden voor wanneer een antwoordpatroon als “afwijkend” kan worden beschouwd. Wij hebben één van de methoden van Van Krimpen-Stoop en Meijer (2002) gebruikt die veelvuldig gebruikt wordt in de literatuur. We hebben duizend item-responses gesimuleerd conform het 2PL-model (het IRT-model gehanteerd in de ACT): dit stelde ons in staat om de waarden van C^– en C⁺ te bepalen die men mag verwachten bij antwoordpatronen conform het IRT-model. Vervolgens is een bootstrapprocedure (met 1000 hertrekkingen met teruglegging) uitgevoerd om de steekproefverdelingen van het 5^e percentiel (C^–) en het 95^ste percentiel (C⁺) te benaderen (de bootstrapverdelingen). De medianen van deze verdelingen bepaalde vervolgens de aftestgrenzen.

Uiteindelijk betekende dit dat een antwoordpatroon als afwijkend werd aangeduid wanneer C⁺ boven de .2286 uitkwam bij Cijferreeksen, bij Figurenreeksen boven de .2618 en bij Verbale Analogieën boven de . 2366. Voor C^– gold dat een antwoordpatroon afwijkend was wanneer deze lager was dan -.2339 bij Cijferreeksen, -.2616 bij Figurenreeksen en -.2429 bij Verbale Analogieën.

6.10.2.2. Aantal Guttman fouten

Als tweede maat hebben we gekozen voor het aantal Guttman fouten (1950). Het voordeel van deze maat is dat het een simpele en intuïtieve maat is, en omdat er is aangetoond dat deze maat goed is in het detecteren van inconsistente antwoordpatronen (Meijer, 1994). IRT schrijft voor dat een persoon die een item met moeilijkheid (b) -1 goed heeft, een item met moeilijkheid -1.5 ook goed heeft. Een Guttman fout is een respons die niet in overeenstemming is met het IRT-model. Dit is het makkelijkst te illustreren met een voorbeeld. Een denkbeeldig persoon heeft 5 items met b-waarden (gerangschikt van moeilijk naar makkelijk) 2, 1, 0.5, 0, -0.1 gemaakt met het volgende responspatroon 11010. Deze persoon heeft één Guttman fout gemaakt: het vierde – relatief makkelijkere – item (b = 0) heeft hij/zij goed, terwijl hij/zij het derde – relatief moeilijkere – item (b = 0.5) fout heeft. Dit antwoordpatroon is daarom niet conform het model. Het aantal Guttman fouten is afhankelijk van de lengte van iemands responspatroon (Meijer, 1994). Omdat in de ACT Algemene Intelligentie verschillende personen een verschillend aantal items kunnen krijgen, hebben we daarom gebruik gemaakt van de genormeerde maat, die hiervoor corrigeert. Deze maat loopt van 0 tot 1 waarbij 0 ‘geen person misfit’ betekent en 1 een scorepatroon wat geheel afwijkend is van wat men mag verwachten op basis van het IRT-model.

Deze maat is een non-parametrische statistiek en kent dus geen (theoretische) steekproefverdeling. Om toch een kritieke waarde te kunnen bepalen waarbij we het aantal Guttman fouten als ‘te hoog’ beschouwen (en dus het antwoordpatroon als “afwijkend”) is net als bij de aftestgrenzen van de CUSUM-procedure eenzelfde bootstrapprocedure gebruikt. Voor Cijferreeksen gold dat een waarde ≥ .8184 als afwijkend beschouwd kon worden, bij Figurenreeksen ≥ .7890 en bij Verbale Analogieën ≥ .8764.

6.10.3. Verwachtingen

Aan de hand van de bovengenoemde aftestgrenzen is bepaald hoeveel procent van de steekproef een afwijkend antwoordpatroon liet zien. Een tweede toepassing van person fit-statistieken is het onderscheiden van groepen die afwijkend antwoordgedrag laten zien: als bepaalde groepen (bijvoorbeeld mannen ten opzichte van vrouwen) stelselmatig meer afwijkende antwoordpatronen laten zien, dan zouden hun behaalde scores minder valide zijn dan van de andere groepen. Daarom zijn ook de person fit-waarden van verschillende groepen met elkaar vergeleken.

Voor de validiteit van de antwoordpatronen – en dus de schattingen van θ – zouden er geen verschillen moeten zijn in de C^– en C⁺-waarden op basis van geslacht en etniciteit (allochtoon/autochtoon).

Bij de variabele opleidingsniveau ligt dit iets anders: we mogen verwachten dat mensen met een hoger opleidingsniveau een hoger intelligentieniveau hebben dan mensen met een lager opleidingsniveau. Een kenmerk van de ACT is dat de kans dat je een item goed hebt in principe ongeveer 50% is; echter, de ACT begint op een moeilijkheid van -0.5, dus voor hoger opgeleiden (met hogere θ’s) zullen de kansen aan het begin veel hoger liggen. Mensen met een hoger opleidingsniveau (hogere θ) zullen dus eerst een aantal items goed hebben en dus geen negatieve residuen hebben, waardoor C^– aan het begin van de reeks langer op 0 zal blijven staan. Dit zal resulteren in uiteindelijk een lagere C^– dan lager opgeleiden. Een voorspelling voor C⁺ is minder makkelijk te maken: na een aantal items zullen de kansen op het goed beantwoorden voor hoger opgeleiden ongeveer op 50% liggen, en dus zowel negatieve als positieve residuen voorkomen. Ook zullen lager opgeleiden sneller vragen krijgen waarbij zij 50% kans hebben om het goed te hebben, waardoor het onduidelijk is of hun C⁺ hoger of lager uit zal vallen dan hoger opgeleiden.

Wat betreft het aantal Guttman fouten zou het de validiteit van de ACT Algemene Intelligentie ondersteunen als er geen verschillen gevonden worden wat betreft geslacht, etniciteit en opleidingsniveau.

Omdat de item-parameters op de gehele steekproef (bestaande uit personen uit de kalibratiesteekproef en ‘echte’ kandidaten uit het Ixly-systeem) zijn gekalibreerd, zijn de analyses gedaan voor deze totale steekproef en de kandidaatssteekproef.

6.10.4. Resultaten

 De analyses zijn gedaan op zowel de totale steekproef (kalibratiesteekproef en kandidaatssteekproef) als de kandidaatssteekproef. Informatie over achtergrondkenmerken is te vinden in sectie 6.8.

6.104.1. CUSUM: aantal afwijkende antwoordpatronen en verschillen tussen groepen

Omdat we het 95^ste percentiel hebben gehanteerd is een percentage van 5% ‘afwijkende’ antwoordpatronen acceptabel. Echter, de percentages onder/boven de kritieke waarden van respectievelijk C^– en C⁺ waren over het algemeen kleiner (Tabel 6.54.).

Tabel 6.54. Percentage afwijkende antwoordpatronen op basis van CUSUM-procedure.
	Totale   steekproefa	Kandidaats-   steekproefb
Cijferreeksen	3.4	1.3
Figurenreeksen	5.3	2.3
Verbale Analogieën	3.6	3.8
a N = 5079-5238.   b N = 2532-2534.

In Tabel 6.55. zijn de percentages afwijkende antwoordpatronen weergegeven voor verschillende groepen. Opvallend is dat de percentages aanzienlijk hoger zijn in de totale steekproef dan in de data verkregen in bij ‘echte’ gebruikers van de test. De totale steekproef bestond voor een deel uit personen die voor een vergoeding meededen aan onderzoek (namelijk de personen uit de kalibratiesteekproef): het is dus goed mogelijk dat zij de items minder serieus beantwoord hebben, wat terug te zien is in de hogere percentages afwijkende scorepatronen.

Op basis van χ²-toetsen is onderzocht of de proporties afwijkende scorepatronen verschilden op basis van etniciteit[17], geslacht en opleidingsniveau. Er werden geen significante verschillen gevonden tussen allochtonen en autochtonen, en ook niet tussen mannen en vrouwen in de kandidaatsteekproef (Tabel 6.55.). Wel waren er verschillen tussen mannen en vrouwen in de totale steekproef (Figurenreeksen) en tussen de opleidingsniveaus (Figurenreeksen en Verbale Analogieën).

Tabel 6.55. Percentage afwijkende antwoordpatronen op basis van CUSUM-procedure, naar etniciteit, geslacht en opleidingsniveau.
	Etniciteit			Geslacht					Opleidingsniveau
	Kalibratiesteekproef			Totaal		Kandidaats			Kandidaats
	Autochtoona	Allochtoona		Manb	Vrouwb	Manc	Vrouwc		VMBOd	MBOd	HBOd	WOd
Cijferreeksen	5.4	5.1		3.2	3.9	1.4	1.1		1.5	1.4	1.0	.3
Figurenreeksen	8.2	10.5		4.8*	6.5*	2.2	2.4		3.9	3.0**	.8**	.6**
Verbale Analogieën	3.2	4.2		3.9	3.5	4.1	4.2		6.9**	4.8**	2.7	1.2**
** p < .01  (2-zijdig). a Nautochtoon = 2226-2359, Nallochtoon = 296-331.b Nmannen = 2507-2587, Nvrouwen = 2212-2307.c Nmannen = 1456-1457, Nvrouwen = 746-748.d NVMBO = 203, NMBO = 1093-1094, NHBO = 399-401, NWO = 326-327.

Om een beeld te krijgen van de grootte van de verschillen is bij het verschil tussen mannen en vrouwen gekeken naar Cohen’s d als maat van effectgrootte en bij opleidingsniveau naar η². Bij de Figurenreeksentest was het verschil tussen mannen en vrouwen in de totale steekproef klein (d = -.07). Het verschil op basis van opleidingsniveau was zowel bij Figurenreeksen als bij Verbale Analogieën zeer klein (η² = .007). Bij Figurenreeksen was er alleen een significant verschil tussen de MBO- en HBO-groep, bij Verbale Analogieën week het percentage afwijkende patronen significant af van het percentage bij de VMBO- en MBO-groep.

Op basis van deze resultaten kunnen we concluderen dat er relatief weinig afwijkende antwoordpatronen waarneembaar zijn bij de ACT Algemene Intelligentie. Ook zijn er weinig of kleine verschillen gevonden tussen groepen. Alleen de VMBO-groep laat iets meer afwijkende scorepatronen zien dan we op basis van kans zouden mogen verwachten. Dit betekent dat de verkregen antwoordpatronen/scores op de ACT Algemene Intelligentie als valide beschouwd kunnen worden.

6.10.4.2. CUSUM: verschillen tussen groepen in C^– en C⁺

Wat betreft de C^–-waarden hebben we geen significante verschillen gevonden tussen autochtonen en allochtonen. Dit betekent dat allochtonen niet vaker dan autochtonen een vraag fout hebben dan we op basis van het model mogen verwachten. Voor C⁺ vinden we kleine marginaal significante verschillen tussen allochtonen en autochtonen voor Figurenreeksen (d = -.11, p = .09) en Verbale Analogieën (d = -.12, p = .05). Uit het minteken en het plusteken van de effectgrootten d is te concluderen dat allochtonen bij de Figurenreeksen ‘benadeeld’ zijn, en bij Verbale Analogieën ‘bevoordeeld’. Over het algemeen kunnen we echter concluderen dat er geen verschillen wat betreft etniciteit zijn in de consistentie van antwoordpatronen (en dus de θ-schattingen).

Tabel 6.56. Verschillen in C– en C+ naar etniciteit.
	C–						C+
	Autochtoon		Allochtoon		d		Autochtoon		Allochtoon		d
	M	SD	M	SD			M	SD	M	SD
Cijferreeksen	-.16	.05	-.16	.05	.08		.16	.05	.15	.05	.06
Figurenreeksen	-.18	.05	-.18	.04	.05		.17	.06	.18	.06	-.11†
Verbale Analogieën	-.14	.05	-.14	.05	-.02		.13	.05	.13	.07	.12*
*p <.05  (2-zijdig), ** p < .01  (2-zijdig).   Nautochtonen = 2222-2355, Nallochtonen = 296-331 (Kalibratiesteekproef).

Tussen mannen en vrouwen vonden we voor C^– alleen significante verschillen bij Figurenreeksen en Verbale Analogieën, bij zowel de totale steekproef als de kandidaatssteekproef. De grootten van de verschillen waren klein volgens de richtlijnen van Cohen (1988). Bij Figurenreeksen hadden mannen wat hogere C^–-waarden, bij de Verbale Analogieën juist wat lagere waarden. Voor C⁺-waarden vonden we alleen een klein significant verschil voor Figurenreeksen in de totale steekproef. Over het algemeen kunnen we dus concluderen dat de antwoordpatronen van mannen en vrouwen even consistent zijn.

Tabel 6.57. Verschillen in C– en C+ naar geslacht.
	Totaala						Kandidaatsb
	Man		Vrouw		d		Man		Vrouw		d
C–	M	SD	M	SD			M	SD	M	SD
Cijferreeksen	-.16	.05	-.16	.05	.05		-.16	.05	-.16	.05	.01
Figurenreeksen	-.17	.05	-.17	.05	.06*		-.17	.05	-.17	.05	.09*
Verbale Analogieën	-.14	.05	-.14	.05	-.08**		-.15	.06	-.14	.06	-.11*
C+
Cijferreeksen	.15	.04	.15	.04	-.02		.15	.03	.15	.03	.07
Figurenreeksen	.17	.05	.17	.06	-.06*		.16	.04	.16	.04	.05
Verbale Analogieën	.14	.05	.14	.05	.00		.15	.04	.15	.04	.03
*p < .05  (2-zijdig), **p < .01  (2-zijdig). a Nmannen = 2507-2586 Nvrouwen = 2211-2304.b Nmannen = 1456-1457, Nvrouwen = 746-748.

Tabel 6.58. laat de verschillen in C^– en C⁺ zien tussen de verschillende opleidingsniveaus. Zoals voorspeld nemen de C^–-waarden af bij hogere opleidingsniveaus, bij alle drie de subtests. De verschillen zijn groot te noemen (η², laatste kolom). Er is ook een negatieve relatie tussen opleidingsniveau en de hoogte van C⁺-waarden, voor de Figurenreeksen en Verbale Analogieën: de WO-groep heeft significant lagere waarden dan de VMBO- en MBO groepen. De verschillen zijn kleiner dan bij de C^–-waarden, afgaande op de effectgrootten.

Zoals hierboven beschreven kunnen deze verschillen niet toegeschreven worden aan een gebrek aan validiteit, maar zijn zij het gevolg van de adaptieve procedure van de ACT in combinatie met het feit dat opleidingsniveau samenhangt met intelligentie.

Tabel 6.58. Verschillen in C– en C+ naar opleidingsniveau.
	VMBOa		MBOa		HBOa		WOa		η2
	M	SD	M	SD	M	SD	M	SD
C–
Cijferreeksen	-.18b	.04	-.17c	.04	-.15b,c,d	.05	-.13b,c,d	.05	.122**
Figurenreeksen	-.19b	.04	-.18c	.04	-.16b,c,d	.05	-.13b,c,d	.05	.147**
Verbale Analogieën	-.17b	.04	-.17c	.05	-.12b,c	.06	-.10b,c	.05	.217**
C+
Cijferreeksen	.15b	.03	.15c	.03	.15b,c	.04	.15	.04	.006**
Figurenreeksen	.16b	.03	.16c	.04	.16	.04	.15b,c	.04	.014**
Verbale Analogieën	.16b	.04	.16c	.04	.14b,c	.04	.13b,c	.04	.064**
** p < .01  (2-zijdig).   a NVMBO = 203, NMBO = 1093-1094, NHBO = 399-401, NWO = 326-327.

6.10.4.3. Aantal Guttman fouten: aantal afwijkende antwoordpatronen en verschillen tussen groepen

 Analoog aan de analyses voor de C^– en C⁺-waarden hebben we eerst gekeken naar ‘te hoge’ waarden voor het aantal Guttman fouten: omdat we het 95^ste percentiel hebben gehanteerd is een percentage van 5% ‘afwijkende’ antwoordpatronen acceptabel. De percentages zijn echter, zoals weergegeven in Tabel 6.59, zeer klein. De gegeven antwoordpatronen zijn dus nauwelijks afwijkend te noemen op basis van het aantal Guttman fouten.

Tabel 6.59. Percentage afwijkende antwoordpatronen   op basis van het aantal Guttman fouten.
	Totale   steekproefa	Kandidaats-   steekproefb
Cijferreeksen	0.32	0.04
Figurenreeksen	1.05	0.20
Verbale Analogieën	0.38	0.28
a N = 5039-5270.   b N = 2526-2556.

Ook hebben we weer gekeken naar de verschillen tussen groepen wat betreft het aantal Guttman fouten: deze zijn weergegeven in Tabel 6.60.

Tabel 6.60. Percentage afwijkende antwoordpatronen op basis van het aantal Guttman fouten, naar etniciteit, geslacht en opleidingsniveau.
	Etniciteit			Geslacht					Opleidingsniveau
	Kalibratiesteekproef			Totaal		Kandidaats			Kandidaats
	Autochtoona	Allochtoona		Manb	Vrouwb	Manc	Vrouwc		VMBOd	MBOd	HBOd	WOd
Cijferreeksen	0.51	1.20		0.27	0.43	0.00	0.13		0.00	0.00	0.25	0.00
Figurenreeksen	1.77	2.73		1.09	1.13	0.34	0.00		0.99	0.09	0.00	0.31
Verbale Analogieën	0.43	1.03		0.37	0.37	0.21	0.27		0.00	0.09	0.50	0.31
a Nautochtoon = 2202-2366, Nallochtoon = 293-332.   b Nmannen = 2480-2596, Nvrouwen = 2212-2319. c Nmannen = 1453-1463, Nvrouwen = 746-754. d NVMBO = 203-205, NMBO = 1093-1097, NHBO = 398-406, NWO = 324-329.

Bij de χ²-toetsen vonden we geen significante verschillen wat betreft etniciteit, geslacht en opleidingsniveaus: echter, omdat de aantallen die aangemerkt werden als ‘afwijkend’ zo laag waren, moeten hier niet te sterke conclusies aan verbonden te worden.

6.10.4.4. Aantal Guttman fouten: verschillen tussen groepen

 Significante verschillen werden gevonden tussen allochtonen en autochtonen voor de Cijferreeksen en Figurenreeksen-test; allochtonen lieten over het algemeen iets meer afwijkende scorepatronen zien dan autochtonen, hoewel de effectgrootten kleine effecten aanduidden.

Tabel 6.61. Verschillen in het aantal Guttman fouten naar etniciteit.
	Autochtoon		Allochtoon		d
	M	SD	M	SD
Cijferreeksen	.26	.16	.29	.18	-.22**
Figurenreeksen	.33	.18	.35	.18	-.13*
Verbale Analogieën	.23	.15	.24	.16	-.06
* p <.05  (2-zijdig), ** p < .01  (2-zijdig).   Nautochtonen = 2115-2311, Nallochtonen = 292-323.

Bij de totale steekproef (zowel de kalibratiesteekproef als ‘echte’ kandidaten uit het Ixly-systeem) werden kleine significante verschillen gevonden voor alle drie de subtests: vrouwen lieten over het algemeen iets meer afwijkende scorepatronen zien dan mannen. Bij de steekproef die alleen bestond uit personen die de adaptieve test hadden gemaakt in echte selectiesituaties werden geen verschillen tussen mannen en vrouwen gevonden (Tabel 6.62.).

Tabel 6.62. Verschillen in het aantal Guttman fouten naar geslacht.
	Totaala						Kandidaatsb
	Man		Vrouw		d		Man		Vrouw		d
	M	SD	M	SD			M	SD	M	SD
Cijferreeksen	.21	.16	.22	.16	-.09**		.16	.14	.16	.14	.05
Figurenreeksen	.25	.18	.28	.18	-.14**		.19	.16	.18	.15	.06
Verbale Analogieën	.20	.17	.21	.16	-.08**		.18	.17	.19	.18	-.05
** p < .01  (2-zijdig).   a Nmannen = 2462-2550, Nvrouwen = 2145-2778. b Nmannen = 1448-1454, Nvrouwen = 746.

Wat betreft opleidingsniveaus vonden we alleen significante verschillen in het aantal Guttman fouten bij Verbale Analogieën. De VMBO- en MBO-groep enerzijds vertoonden meer afwijkende antwoordpatronen dan de HBO- en WO-groep anderzijds; ook duidde de effectgrootte echter een klein effect aan (Tabel 6.63).

Tabel 6.63. Verschillen in het aantal Guttman fouten naar opleidingsniveau.
	VMBOa		MBOa		HBOa		WOa		η2
	M	SD	M	SD	M	SD	M	SD
Cijferreeksen	.15	.13	.16	.13	.16	.15	.16	.15	.001
Figurenreeksen	.19	.17	.19	.15	.17	.15	.20	.17	.001
Verbale Analogieën	.20c	.16	.20d	.16	.15c,d	.18	.14c,d	.19	.019**
** p < .01  (2-zijdig).   a NVMBO = 202-203, NMBO = 1092-1094, NHBO = 398-401, NWO = 320-326.

De bevindingen van het aantal Guttman fouten staan in contrast met de bevindingen voor de CUSUM-procedure wat betreft opleidingsniveau: echter, zoals al eerder geduid, is dit te verklaren door de specifieke kenmerken van de CUSUM-procedure op basis waarvan we juist verschillen tussen opleidingsniveaus mogen verwachten.

6.10.5. Conclusies person fit

 In dit onderzoek is aangetoond dat we op basis van twee maten – C^– en C⁺ uit de CUSUM-methode en het aantal Guttman fouten – weinig afwijkende antwoordpatronen zien bij de ACT Algemene Intelligentie. Personen lieten dus antwoordpatronen zien die consistent zijn met het gekozen IRT-model. Omdat op basis van het antwoordpatroon iemands score wordt bepaald ondersteunen deze bevindingen dus de validiteit van de verkregen testscores op individueel niveau.

Ook vonden we weinig of kleine verschillen tussen verschillende groepen wat betreft achtergrondkenmerken (etniciteit, geslacht en opleidingsniveau). Dit betekent dat de scores van deze verschillende groepen als even valide beschouwd kunnen worden. Hiermee draagt dit onderzoek bij aan de validiteit van de verkregen testscores van de ACT Algemene Intelligentie.

6.11. Algemene conclusie begripsvaliditeit

De in dit hoofdstuk (en sectie 1.5.1.) beschreven resultaten bieden duidelijk bewijs voor de begripsvaliditeit van de ACT Algemene Intelligentie. Allereerst is de goede mate van item-fit en de fit van het gekozen IRT-model een indicatie voor de validiteit van het gebruikte model. Aan de hand van de intercorrelaties tussen de subtests hebben we convergente validiteit en unidimensionaliteit aangetoond. Dit bleek bovendien uit een onderzoek waar een model met één factor vergeleken werd met een twee-factoren model. Bovendien bleef de structuur van de drie subtests overeind bij verschillende groepen. In diverse onderzoeken werd verder bewijs voor de veronderstelde g-factor in de ACT Algemene Intelligentie gevonden. Aan de hand van relaties met persoonlijkheid hebben we ook divergente validiteit van de ACT Algemene Intelligentie aangetoond. Convergente validiteit werd in dit onderzoek ook aangetoond (met de factor Openheid), evenals in twee onderzoeken naar de relaties met begrijpend lezen en reactietijden.

Soortgenotenvaliditeit werd aangetoond in een onderzoek met de MCT-H (Bleichrodt & Van den Berg, 1997, 2004): de correlaties tussen de subtests van de ACT Algemene Intelligentie en de subtests van de MCT-H waren hoog (gemiddeld .60, gecorrigeerd voor (on)betrouwbaarheid gemiddeld .74). De g-scores waren nauwelijks van elkaar te onderscheiden: de correlaties tussen de g-score gebaseerd op de ACT Algemene Intelligentie en de g-score gebaseerd op de MCT-H was .80 (.95 na correctie voor (on)betrouwbaarheid). Structurele modellen toonden verder aan dat de structuur van de twee tests sterk overeenkwamen, net als de sterke de overlap tussen de twee g-scores (r = .99).

Verschillen in intelligentie die we op basis van opleidingsniveau mogen verwachten ook teruggevonden worden bij de ACT Algemene Intelligentie. Dit geeft aan dat verschillen in scores op de ACT Algemene Intelligentie samen lijken te gaan met reële verschillen tussen groepen en dat het beoogde construct – intelligentie – inclusief deze reële verschillen tussen groepen, wordt gemeten. Dit gold ook voor de verschillen op basis van leeftijd, waarbij voorspelling over de relatie tussen leeftijd en intelligentie grotendeels bevestigd werden met de ACT Algemene Intelligentie; deze conclusie gold ook voor de gevonden verschillen op basis van geslacht. De gevonden verschillen wat betreft leeftijd en geslacht waren overigens in alle gevallen klein tot gemiddeld: dit betekent dat de ACT Algemene Intelligentie voor alle leeftijdsgroepen en voor zowel mannen als vrouwen gebruikt kan worden.

Het feit dat autochtonen en allochtonen niet van elkaar leken te verschillen wat betreft hun θ’s voor de Figurenreeksentest bevestigt verder dat deze subtest het meest cultuurvrij is van de drie subtests, zoals we op basis van de literatuur voorspeld hadden. De verschillen op basis van etniciteit waren van kleine tot gemiddelde omvang; bij de interpretatie van de scores zou dit in ogenschouw genomen kunnen worden (zie ook Hoofdstuk 4 hierover).

Onderzoek naar differential item functioning (DIF) en differential test functioning (DTF) toonde verder aan dat we op basis van leeftijd, geslacht en etniciteit weinig vertekeningen in itemresponses mogen verwachten bij de ACT Algemene Intelligentie. Dit is een belangrijke bevinding in relatie tot de fairness van de test: dit onderzoek toonde aan dat de test bij verschillende groepen ingezet kan worden. Deze conclusie is ook van toepassing op het onderzoek naar person fit: er waren maar weinig personen die – vergeleken met het theoretisch veronderstelde model – afwijkende scorepatronen lieten zien. Bovendien waren er weinig verschillen in het aantal afwijkende scorepatronen op basis van geslacht, opleidingsniveau en etniciteit.

[1] Modellen met meerdere factoren hebben wij niet getoetst; door het groot aantal items, personen en missende waarden en het feit dat IRTPRO een schatter met full information maximum likelihood gebruikt, duurde het schatten van een model met twee factoren al een aantal uren. Bij multidimensionele IRT met meerdere factoren neemt de schattingstijd exponentieel toe.

[2] In verband met itembekendheid laten we hier in het midden wat deze logica precies is.

[3] Deze communaliteit is berekend door de som van de gekwadrateerde ladingen op de algemene factor te delen door de som van alle gekwadrateerde ladingen.

[4] Deze analyses zijn gedaan op de tetrachorische correlatiematrix (omdat de gegeven antwoorden binair (0-1) zijn) met behulp van het psych-pakket (Revelle, 2016) in R (R Core Team, 2016).

[5] De analyses zonder dataset 6 lieten vergelijkbare fit-waarden zien.

[6] CFI < .85 slechte fit, .85 < CFI < .89 middelmatige fit, .90 < CFI < .95 acceptabele fit, .95 < CFI < .99 zeer goede fit, 1 exacte fit. RMSEA ≤ .05 goede fit, hoewel ook waarden van .08 gehanteerd worden.

[7] Een formele toetsing van het verschil in χ²-waarden tussen modellen 1/2 en 3 is problematisch bij geïmputeerde datasets (Muthén, 2013).

[8] Verdeeld in de vier categorieën 15 tot 25, 25 tot 40, 40 tot 55 en 55 tot en met 65.

[9] In dit onderzoek hadden wij geen toegang tot de ruwe scores waardoor wij zelf de betrouwbaarheden niet konden berekenen van de subtests.

[10] Een aantal kandidaten had zeer veel fouten gemaakt. Daarom zijn de analyses ook uitgevoerd zonder deze uitbijters. De resultaten en conclusies bleven gelijk; gemiddeld over de vier onderdelen van de ACT Algemene Intelligentie veranderden de correlaties uit Tabel 6.32. nauwelijks (ongeveer .03 tot .05).

[11] Hiervoor is gebruik gemaakt van de spreadsheet van Jamie DeCoster via http://www.stat-help.com/spreadsheets.html.

[12] De 27 personen die zelf in het buitenland zijn geboren maar waarvan beide ouders in het buitenland zijn geboren hebben wij ook tot de allochtone groep gerekend (5.0% van het totaal aantal allochtonen). T-toetsen lieten zien dat deze groep niet verschilde in hun scores op de ACT Algemene Intelligentie van de andere allochtonen.

[13] De regressiecoëfficiënten uit de drie modellen kunnen ook geanalyseerd worden om een beeld te krijgen van welke groep bevoordeeld of benadeeld is. Omdat de gevonden effecten over het algemeen klein waren en er niet duidelijk één groep bevoordeeld of benadeeld werd hebben we ter wille van de eenvoud deze methode hier niet uitgebreid beschreven. Voor leeftijd doen we dit wel omdat we hier meer effecten vonden en omdat hiervoor een indeling in ETS categorieën niet mogelijk was.

[14] Zumbo (1999) beveelt een significantieniveau van .01 aan omdat meerdere hypotheses getoetst worden. Wij hanteren echter een strenger niveau van .05: bij dit significantieniveau worden items immers eerder als potentiële DIF items gekenmerkt dan bij een niveau van .01.

[15] Er zijn DTF analyse methoden gebaseerd op IRT-modellen maar om redenen uitgelegd in de sectie Huidig onderzoek hebben wij niet voor deze methoden gekozen.

[16] Voor de verwachte scores hebben we ook predictie intervallen berekend en deze voor iedere groep geplot. Alle intervallen bleken te overlappen, wat betekent dat er geen verschillen waren in verwachte scores tussen groepen. Om de figuren overzichtelijk te houden hebben we de intervallen niet weergegeven.

[17] Op het moment van schrijven was alleen informatie beschikbaar over etniciteit bij de kalibratiesteekproef. Vandaar dat deze analyses alleen op deze steekproef zijn gedaan wat betreft etniciteit.

 

 

7. Criteriumvaliditeit

Bij criterium- of predictieve validiteit gaat het om de voorspellende waarde van testscores (Cotan, 2009). Om de criteriumvaliditeit te bepalen zijn er onderzoeken uitgevoerd waarbij gekeken is naar de relatie tussen de ACT Algemene Intelligentie en verschillende constructen uit verschillende domeinen. Deze zullen hieronder besproken worden.

In dit hoofdstuk wordt eerst een onderzoek besproken naar de relaties tussen scores op de ACT Algemene Intelligentie en een aantal uitkomstmaten waarvan herhaaldelijk aangetoond is dat zij voorspeld kunnen worden door intelligentie. Een deel van deze uitkomstmaten – namelijk die gerelateerd aan werk – zijn hierbij met name van belang gezien het testdoel van de ACT Algemene Intelligentie (voor selectiedoeleinden) en het werkveld waarvoor de test ontwikkeld is (HRM, selectie- en assessment).

In sectie 7.2. wordt een onderzoek beschreven naar de relatie tussen intelligentie en academische prestaties. Gezien het eerder genoemde testdoel en beoogde werkveld lijken deze resultaten wellicht minder relevant. Echter, academische prestaties blijken sterk samen te hangen met werkprestaties; academische prestaties worden daarom in wetenschappelijk onderzoek vaak gezien als het equivalent van werkprestaties maar dan toegespitst op studenten/de universiteit (Kuncel, Hezlett, & Ones, 2004). Bijvoorbeeld, university citizenship behavior (Gehring, 2006; Zettler, 2011) en counterproductive academic behavior (Marcus, Lee, & Ashton, 2007; Zettler, 2011) zijn de tegenhangers van organizational citizenship behavior (Chiaburu, Oh, Berry, Li, & Gardner; Katz, 1964; Organ, 1988) en counterproductive work behavior (Rotundo & Spector, 2010). Dit komt doordat factoren (bijv. motivatie, persoonlijkheid, intelligentie) die verondersteld worden academische prestaties te beïnvloeden ook werkprestatie lijken te beïnvloeden (Kuncel et al., 2004). Zodoende kan dit onderzoek dan ook bijdragen aan de criteriumvaliditeit van de ACT Algemene Intelligentie.

Hoewel deze onderzoeken niet afgenomen zijn onder dezelfde condities als waar de test voor bedoeld is (namelijk selectiesituaties) kunnen deze gegevens toch bijdragen aan de criteriumvaliditeit van de ACT Algemene Intelligentie. Ten eerste is het niet ongebruikelijk om studenten of andere populaties dan de doelpopulaties te gebruiken bij de ontwikkeling en validering van psychologische tests (bijvoorbeeld bij de FFPI: Hendriks, 1997; Hendriks, Hofstee, De Raad, & Angleiter, 1999). Bovendien was er bij het eerste onderzoek een testleider aanwezig waardoor het maken van een test in een testzaal voor een deel nagebootst werd – hierdoor is het aannemelijk dat de kandidaten de test serieus hebben ingevuld.

Een laatste opmerking heeft betrekking op de steekproef van het onderzoek beschreven in sectie 7.1. Deze steekproef is dezelfde steekproef als waar de soortgenotenvaliditeit mee onderzocht is (sectie 6.5.1.). Omdat het hier verschillende soorten validiteit betreft hebben we ervoor gekozen de onderzoeken in verschillende hoofdstukken te beschrijven. De onderzoeksprocedure en kenmerken van de steekproef worden beschreven in sectie 6.5.1.2.

7.1. Onderzoek naar gezondheid, sociaaleconomische status, werk en schoolprestaties

‘Algemene intelligentie’ is een zeer brede competentie die mensen het vermogen geeft problemen op te lossen, connecties te maken tussen dingen, abstract te denken, complexe ideeën te begrijpen en snel te leren, ook van eerdere ervaringen (Gottfredson, 1997, p. 13). Hiermee is het dus een zeer algemene functionele competentie, die mensen in staat stelt algemeen gewaardeerde doelen te bereiken (Gottfredson, 1997). Daarom kunnen we verwachten dat het invloed heeft op een breed scala aan levensdomeinen, waaronder algemene gezondheid (Gottfredson, 2004), het behalen van een hogere sociaaleconomische status (Strenze, 2007), werkkenmerken (bijvoorbeeld werkcomplexiteit; Gottfredson, 1997) en prestaties op het werk (Schmidt & Hunter, 2004). De relaties tussen scores op de ACT Algemene Intelligentie en bovenstaande uitkomsten zijn onderzocht om bewijs te leveren voor de criteriumvaliditeit van de ACT Algemene Intelligentie.

7.1.1. Hypothesen

Gezondheid

Er is een verband tussen intelligentie en gezondheid gelegd, en dan met name op het gebied van leefgewoonten, kans op ziekten en de levensverwachting van een persoon (Gottfredson, 2004; Gottfredson & Deary, 2004). Over het algemeen wordt bijvoorbeeld een zwakke negatieve relatie gevonden tussen intelligentie en ongezonde leefgewoonten zoals roken (Gottfredson & Deary, 2004). Op basis hiervan verwachtten we een zwakke relatie tussen intelligentie en rookgedrag.

Sociaaleconomische status

De sociaaleconomische status van een persoon zegt iets over zijn of haar plek in de maatschappij, of zijn of haar plek op de ‘sociale ladder’: belangrijke indicatoren hiervan zijn het behaalde opleidingsniveau, beroep en inkomen.

De relatie tussen intelligentie en behaald opleidingsniveau is evident en talrijke keren aangetoond (zie bijvoorbeeld Ceci, 1991; Herrnstein & Murray, 1994; Neisser et al., 1996, Sewell & Shah, 1967). Op basis van de meta-analyse van Strenze (2007) mogen we een sterk effect van intelligentie op het behaalde opleidingsniveau verwachten (ongeveer r = .46).

Een groot aantal studies heeft een positieve directe relatie aangetoond tussen intelligentie en inkomen (bijvoorbeeld Ceci & Williams, 1997; Heckman, Stixrud, & Urzua, 2006; Herrnstein & Murray, 1994; Scullin, Peters, Williams, & Ceci, 2000). Redelijk recente meta-analyses toonden aan dat de correlatie tussen inkomen en intelligentie rond de .21 (Strenze, 2007) en .27 zal liggen (Ng et al., 2005); op basis hiervan kunnen we dus een vergelijkbare correlatie tussen inkomen en de scores op de ACT Algemene Intelligentie verwachten.

Ook de relatie tussen intelligentie en beroepsstatus is overduidelijk aanwezig in de literatuur (zie bijvoorbeeld Judge, Higgins, Thoresen, en Barrick, 1999 en Schmidt en Hunter, 2004 voor overzichtsartikelen). Volgens de meta-analyse van Strenze (2007) mogen we ook hier een sterk effect verwachten (ongeveer .37).

Werkgerelateerde uitkomsten

Schmidt en Hunter hebben in verschillende meta-analyses aangetoond dat intelligentie een sterke voorspeller is voor werkprestaties in een groot aantal banen – sterker dan de effecten van andere voorspellers zoals persoonlijkheid (Schmidt & Hunter, 1998; 2004). Hoewel intelligentie belangrijk lijkt te zijn voor de meeste banen, neemt het effect ervan op werkprestatie toe met de complexiteit van de baan. De validiteitscoëfficiënten variëren tussen de .23 voor banen met de laagste complexiteit tot .58 voor banen met de hoogste complexiteit (Schmidt & Hunter, 2004). We verwachten dus een relatief sterk positief effect van intelligentie op werkprestatie dat toeneemt met werkcomplexiteit (een positief interactie-effect).

Bovenstaande effecten hebben betrekking op taakprestatie: dus prestatie op taken die direct onderdeel zijn van de dagelijkse uitvoering van het werk (ref?). In de literatuur worden echter nog twee andere dimensies van werkprestatie onderscheiden, namelijk contextuele prestatie en contraproductief werkgedrag. Contextuele prestatie heeft betrekking op prestaties die te maken hebben met taken die niet officieel in de functieomschrijving staan, dus bijvoorbeeld het helpen van een collega, of het inbrengen van nieuwe ideeën om het werk te verbeteren (ref?). Contraproductief werkgedrag omvat negatieve gedragingen op het werk, zoals roddelen over een collega of stelen van werkeigendommen. Er is aangetoond dat bij contextuele prestaties zaken als persoonlijkheid een belangrijkere rol spelen dan intelligentie (zie bijvoorbeeld Borman & Motowidlo, 1997), daarom mogen we een kleiner effect van intelligentie verwachten. Het effect van intelligentie op contraproductief werkgedrag is nog onduidelijk (zie Dilchert, Ones, Davis, & Rostow, 2007 en Marcus, Wagner, Poole, Powell, & Carswell, 2009); hier doen we dus geen expliciete voorspellingen over.

Onderzoek heeft ook aangetoond dat intelligentie samenhangt met de kenmerken van het werk dat iemand doet. Zoals hiervoor beschreven is de relatie tussen intelligentie en complexiteit van het werk vaak aangetoond (Schmidt & Hunter, 2004). Deze relatie is vrij logisch, aangezien hetgeen wat het werk complex maakt – de hoeveelheid informatieverwerking die het werk vraagt – precies datgene is wat intelligentere mensen makkelijker afgaat. Verder stelden Wilk en Sackett (1996) dat een hogere intelligentie personen in staat stelt om te groeien naar complexere (en daardoor ook vaak beter betaalde) banen. Een bijkomend effect is dat mensen met een hogere intelligentie ook graag een baan willen die aansluit bij hun intelligentie en dus cognitief meer van hen vraagt (Ganzach, 1998). Op basis van deze bevindingen mogen we een relatie verwachten tussen complexiteit van het werk en intelligentie: de sterkte van het effect is moeilijk te bepalen bij het ontbreken van een meta-analyse op dit gebied (zie Pad A in Figuur 7.1.).

Ganzach (1998) toonde verder interessante relaties aan tussen intelligentie en werktevredenheid, waar complexiteit ook weer een rol in speelt. Ganzach beargumenteerde (en toonde aan) dat intelligentie een direct negatief effect heeft op werktevredenheid: dit omdat intelligente mensen meer complex werk willen, en daardoor – omdat veel banen complexiteit missen – minder tevreden zijn met hun werk. Dit negatieve effect wordt dus alleen zichtbaar wanneer werkcomplexiteit constant gehouden wordt: in het huidige onderzoek toetsen we of we dit aan kunnen tonen met behulp van scores op de ACT Algemene Intelligentie (Pad C in Figuur 7.1.). Tegelijkertijd kunnen we een indirect positief effect via complexiteit verwachten, omdat intelligentere mensen in meer complexe banen werken en complexiteit positief samenhangt met werktevredenheid (Pad B). Omdat het directe en indirecte effect in tegengestelde richting zijn, was het directe effect (oftewel de simpele correlatie tussen intelligentie en werktevredenheid) niet significant. Deze mediatie is weergegeven met de dikgedrukte lijnen in onderstaande figuur: alle bovenstaande effecten zullen in dit onderzoek worden getoetst.

Ganzach (1998) voorspelde verder dat het effect van intelligentie op werkprestatie beïnvloed wordt door de complexiteit van het werk. Omdat complexere banen intelligentere mensen wel kunnen bevredigen, zal bij een hogere complexiteit van het werk, de relatie tussen intelligentie en werktevredenheid minder negatief zijn. Deze relatie is weergeven in de gestippelde pijl in onderstaande figuur en veronderstelt een positief interactie-effect tussen complexiteit en intelligentie op tevredenheid (Pad D). Ook deze relaties zullen getoetst worden in het huidige onderzoek.

Figuur 7.1. Relaties uit Ganzach (1998).

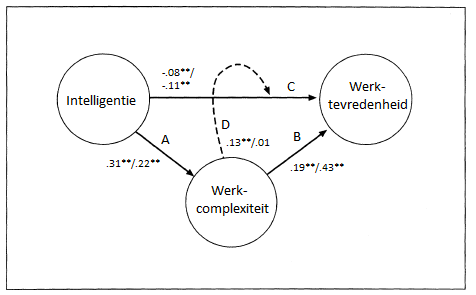
Directe effect van intelligentie op werktevredenheid was -.02. De eerste coëfficiënt (voor het /-teken) is gebaseerd op een model waar de complexiteitsmaat een zelfrapportage was, de tweede coëfficiënt waar dit een objectieve maat was (op basis van functieanalyse).

Schoolprestaties

In de voorgaande bespreking van het effect van intelligentie op sociaaleconomische status hebben we het alleen gehad over het effect op behaald opleidingsniveau. Echter, we kunnen ook een effect verwachten van intelligentie op schoolprestaties (dus bijvoorbeeld behaalde cijfers). Ook hier is veel onderzoek naar gedaan, en hoewel motivatie – voornamelijk gezocht in persoonlijkheidstrekken van personen – ook een belangrijke rol speelt (Poropat, 2009), blijkt intelligentie relatief één van de belangrijkste voorspellers van schoolprestaties (zie Roth et al., 2015 voor een recent overzichtsartikel en meta-analyse). Volgens deze laatste meta-analyse mogen we een sterk effect verwachten (ongeveer r = .44).

7.1.2. Methode

7.1.2.1. Steekproef

Het onderzoek naar de criteriumvaliditeit is gedaan onder dezelfde personen als bij wie het onderzoek naar soortgenotenvaliditeit is afgenomen. Voor meer informatie over de streekproef verwijzen we de lezer door naar sectie 6.5.1.

Voor de analyses die betrekking hebben op het werk van de deelnemers (beroep, inkomen, werkprestatie, cognitieve werkeisen, werktevredenheid) zijn alle studenten verwijderd, omdat zij een atypische groep hierin vormen: we mogen verwachten dat zij zich nog niet op een punt in hun loopbaan bevinden waar deze zaken een belangrijke rol zullen spelen. Deze kleinere steekproef zonder studenten bestond uit 84 personen.

7.1.2.2. Instrumenten

Gezondheid

Rookgedrag

De respondenten werden gevraagd of zij op dit moment rookten. Antwoordmogelijkheden waren “ja, dagelijks”, “ja, af en toe” en “nee, helemaal niet”). Als zij “nee, helemaal niet” antwoordden, werd gevraagd of zij ooit dagelijks hebben gerookt. Op basis van deze antwoorden werden twee variabelen gemaakt. Eén categorische variabele gebaseerd op de drie antwoordmogelijkheden (“ja, dagelijks”, “ja, af en toe” en “nee, helemaal niet”). De laatste variabele was een dichotome variabele “Ooit gerookt”, met score 1 als men nu of ooit gerookt had, en 0 wanneer men nu niet rookte en ook vroeger niet gerookt had.

In Tabel 7.1. en 7.2. zijn de verdelingen van de proefpersonen over deze twee variabelen weergegeven.

Tabel 7.1. Verdeling respondenten over huidig rookgedrag (N = 92).
	Huidig rookgedrag
	Aantal	%
Niet	65	71
Ja, af en toe	10	11
Ja, dagelijks	17	19
Totaal	92	100

 

Tabel 7.2. Verdeling respondenten over huidig en verleden rookgedrag (N = 92).
	Ooit gerookt
	Aantal	%
Nee	38	41
Ja	54	59
Totaal	92	100

Algehele gezondheid

Ook werden de deelnemers gevraagd hun algemene gezondheid te beoordelen waarbij ze zelf een cijfer tussen de 0 en 100 konden geven, 0 betekende een erg slechte gezondheid, 100 een zeer goede.

 Sociaaleconomische status

 Opleidingsniveau

 In Tabel 7.3. staan de opleidingsniveaus van de deelnemers weergegeven. Om de versplintering over verschillende categorieën tegen te gaan is ervoor gekozen de deelnemers in te delen in vijf opleidingscategorieën. Ook deze zijn weergegeven in Tabel 7.3.

Tabel 7.3. Verdeling respondenten over opleidingsniveaus (N = 92).
	Opleidingscategorie
	Laag	Beneden-   gemiddeld	Gemiddeld	Boven-   gemiddeld	Hoog
Lagere school/basisonderwijs	1
VMBO: basisberoepsgerichte leerweg (BB)	6
VMBO: Gemengde leerweg (GL)	2
MBO 1: Assistent beroepsbeoefenaar	1
MBO 2: Medewerker		1
MBO 3: Zelfstandig medewerker		7
VMBO: Theoretische leerweg (TL)		4
HAVO			9
MBO 4: Middenkaderfunctionaris			17
VWO				2
HBO: Oude stijl				14
HBO: Bachelor				10
WO: Bachelor				3
HBO: Master					3
WO: Master					9
WO: Doctorandus					3
Totaal	10	12	26	29	15

 

 Inkomen

Inkomen werd gemeten aan de hand van de volgende vraag: Wat is het totale bruto jaarinkomen (incl. vakantiegeld) van uw huishouden? In totaal waren er 6 antwoordcategorieën, deze zijn weergegeven in Tabel 7.4.

Tabel 7.4. Verdeling respondenten over inkomensniveaus.
	Totale steekproef   (N = 92)		Zonder studenten   (N = 84)
	Aantal	%	Aantal	%
tot 10.000 euro per jaar	12	13	5	6
10.000 tot 20.000 euro per jaar	14	15	14	17
20.000 tot 30.000 euro per jaar	11	12	10	12
30.000 tot 40.000 euro per jaar	20	22	20	24
40.000 tot 50.000 euro per jaar	12	13	12	14
50.000 euro of meer	23	25	23	27
Totaal	92	100	84	100

 

Beroep

Voor het meten van de beroepsstatus van personen (als een proxy voor sociaaleconomische status) hebben we gebruik gemaakt van een classificering van De Vries en Ganzeboom (2008). Zij vergeleken in hun studie een open en gesloten (dus met enkele beroepscategorieën) vragenformat, en concludeerden dat het gesloten format iets betere meetkwaliteiten had dan het open format. Gezien het feit dat het hanteren van categorieën ook nog eens een stuk eenvoudiger is – bij open vragen moeten de antwoorden gecodeerd en gescoord worden met behulp van een scoringstabel –  hebben wij besloten categorieën te hanteren. Omdat er te weinig personen in enkele categorieën bevonden hebben we enkele categorieën samengevoegd. Dit is op inhoudelijke gronden gebeurd (bijvoorbeeld de drie handarbeid categorieën samengevoegd), waarbij ook geprobeerd is het aantal personen in de verschillende categorieën niet te veel van elkaar af te laten wijken. De uiteindelijke categorieën en de verdeling van de respondenten over deze categorieën zijn weergegeven in Tabel 7.5.

Tabel 7.5. Verdeling respondenten over beroepscategorieën.
	Totale steekproef   (N = 92)		Zonder studenten   (N = 84)
	Aantal	%	Aantal	%
Ongeschoolde en geoefende handarbeid   (bv. schoonma(a)k(st)er, inpakker)	16	17
Semi-geschoolde handarbeid   (bv. chauffeur/chauffeuse, fabrieksarbeid(st)er, timmerman, bakker)
Geschoolde en leidinggevende handarbeid   (bv. automonteur, ploegbaas, elektricien)			11	13
Overige hoofdarbeid   (bv. administratief medewerk(st)er, boekhoud(st)er, verko(o)p(st)er, gezinsverzorg(st)er)	14	15	14	17
Middelbaar leidinggevend of commercieel beroep   (bv. hoofdvertegenwoordig(st)er, afdelingsmanager of winkelier)	20	22	19	23
Middelbaar intellectueel of vrij beroep   (bv. leerkracht, kunstena(a)r(es), verpleegkundige, sociaal werk(st)er, beleidsfunctionaris)	28	30	26	31
Hoger leidinggevend beroep   (bv. manager, directeur/directrice, eigenaar/eigenaresse groot bedrijf, leidinggevende ambtenaar)	14	15
Hoger intellectueel of vrij beroep   (bv. architect(e), arts, wetenschappelijk medewerk(st)er, docent(e) wo-hbo, ingenieur)			14	17
Totaal	92	100	84	100

Werkgerelateerde uitkomsten

Werktevredenheid

Om werktevredenheid te meten hebben we de Job in General schaal (JIG; Ironson, Smith, Brannick, Gibson, & Paul, 1989) gebruikt. Deze maat bestaat uit 18 adjectieven waarbij de respondent aan dient te geven of elk adjectief op zijn/haar werk van toepassing zijn. Voorbeelden zijn “Aangenaam” en “Slecht”. Er zijn drie antwoordmogelijkheden: ja, nee, en ?. Deze laatste optie dient aangeklikt te worden door de respondent als hij/zij het niet zeker weet. De optie ? krijgt een score 1, ja antwoorden op een positief woord een score 3 en nee antwoorden op een positief woord een score 0. Voor negatieve woorden is de scoring omgekeerd (ja = 0, nee = 3). De betrouwbaarheid  van de schaal in de huidige steekproef werkenden was .62. Vergeleken met ander onderzoek is dit aan de lage kant (Ironson, Smith, Brannick, Gibson, & Paul, 1989). Dit leek te komen door het feit dat de positieve woorden en negatieve woorden een cluster vormden: een factoranalyse liet zien dat de items uiteenvielen in deze twee factoren. Omdat de verdeling van de schaal erg scheef was met voornamelijk hoge scores (scheefheid:  -2.0, SE = .25; kurtosis: 6.1, SE = .50), is deze variabele tot de derde macht gedaan om hiervoor te corrigeren en de verdeling meer normaal te maken.

Cognitieve werkeisen

Voor cognitieve werkeisen hebben we verschillende instrumenten voor verschillende constructen gebruikt. Deze worden hieronder beschreven.

Als maat van geestelijke belasting hebben we de geestelijke belastingschaal uit de Vragenlijst Beleving en Beoordeling van de Arbeid (VBBA; Van Veldhoven, Meijman, Broersen, & Fortuin, 2002) gebruikt. Deze vragenlijst wordt veel ingezet voor onderzoek naar psychosociale arbeidsbelasting en werkstress in verschillende branches in het kader van arboconvenanten (Van Veldhoven et al., 2002). De schaal bestaat uit 7 items met vier antwoordmogelijkheden (nooit; soms; vaak; altijd). Een voorbeeldvraag is “Moet u op veel dingen tegelijk letten tijdens uw werk?.  De betrouwbaarheid in deze steekproef was goed (α = .83).

Werkdruk is gemeten aan de hand van een schaal van Houtman et al. (1995), uit een monitorstudie naar stress en lichamelijke belasting door het Ministerie van Sociale Zaken en Werkgelegenheid en TNO. Deze schaal is hierna ook gebruikt in wetenschappelijke publicaties (Van Ruysseveldt, Smulders, & Taverniers, 2008). Deze schaal bestaat uit 5 items met vier antwoordcategorieën (nooit; soms; vaak; altijd). Een voorbeelditem luidt “Moet u erg snel werken?” De betrouwbaarheid van de schaal was goed (α = .79).

Gezien de relatief hoge correlatie (r = .50) tussen geestelijke belasting en werkdruk hebben we ook een “Totale werkdruk” variabele gemaakt door deze twee schalen op te tellen.

Een veelgebruikt instrument voor werkkenmerken is de Work Design Questionnaire (WDQ; Morgeson & Humphrey, 2006; Nederlandse vertaling door Gorgievski, Peeters, Rietzschel, & Bipp, 2016), die een aantal domeinen beslaat. Voor dit onderzoek hebben we de vijf schalen van het domein ‘Kenniskarakteristieken’ gebruikt, omdat wij op basis van sectie 7.1.1. mogen verwachten dat ze positief samenhangen met intelligentie. Dit waren de schalen Informatieverwerking (betrouwbaarheid op basis van α = .81), Probleemoplossing (α = .79), Kennisvariatie (α = .83), Taakcomplexiteit (α = .79) en Specialisatie (α = .87). Ieder schaal bestond uit vier items. Voorbeelditems zijn: “Mijn baan vereist dat ik veel informatie volg en in de gaten houd.” (Informatieverwerking), “Mijn baan omvat het omgaan met problemen die ik niet eerder ben tegengekomen.” (Probleemoplossing), “Voor het uitvoeren van mijn baan is een variatie aan kennis en vaardigheden vereist.” (Kennisvariatie), “Mijn baan is zeer gespecialiseerd in termen van doelen,  taken of activiteiten.“ (Specialisme) en “Mijn taak vereist dat ik slechts één taak of activiteit tegelijk doe.” (negatief geformuleerd, Taakcomplexiteit).

Uit Tabel 7.8. blijkt dat de correlaties tussen de schalen onderling vrij hoog waren (gemiddelde r = .55). Daarom is een factoranalyse uitgevoerd (principal axis factoring met varimax rotatie) waarin duidelijk één onderliggende factor naar voren kwam. Deze factor verklaarde 57% van de variantie in de schalen, de eerste eigenwaarde was 3.2, de tweede eigenwaarde .71. De gemiddelde lading was .71. Daarom hebben we een totaalscore “Cognitieve werkeisen” gecreëerd door de som te nemen van de vijf schalen van de WDQ. De betrouwbaarheid van deze totaalscore was hoog (α = .85).

Werkprestatie

 Voor de meting van werkprestatie hebben we gebruik gemaakt van de Individuele Werkprestatie Vragenlijst (IWPV; Koopmans, Bernaards, Hildebrandt, De Vet, & Van der Beek, 2014). In lijn met de drie theoretische dimensies zoals hiervoor beschreven bestaat de vragenlijst uit drie schalen, namelijk taakprestatie (5 items), contextuele prestatie (8 items) en contraproductief werkgedrag (5 items). In dit onderzoek waren de betrouwbaarheden voldoende, respectievelijk .68, .83 en .76). Voorbeelditems zijn: “In de afgelopen drie maanden… lukte het mij om mijn werk zo te plannen, dat het werk op tijd af was.” (Taakprestatie), “… heb ik extra verantwoordelijkheden op me genomen.“ (Contextuele prestatie) en “… heb ik me gericht op de negatieve kanten van een werksituatie, in plaats van op de positieve kanten.” (Contraproductief werkgedrag). Alle items hanteren een vijf-punts Likert-schaal,

De correlatie tussen taakprestatie en contextuele prestatie was significant (r = .29, p < .01). Hoewel niet al te hoog, is er besloten om een gecombineerde Taak/contextuele prestatiemaat te maken door de scores op deze twee schalen op te tellen; dit omdat we ook kunnen verwachten dat de beste werknemer degene is die beiden laat zien. De omgepoolde contraproductieve werkprestatiemaat, dus “productieve werkprestatie”, liet geen significante correlaties zien met de andere twee dimensies van prestatie (zie Tabel 7.8.).

Tabel 7.6. Beschrijvende statistieken van werkgerelateerde variabelen (N = 84).
	Min	Max	Gem.	SD
Totale werkdruk	19	45	33.37	5.67
Geestelijke belasting	14	28	21.52	3.75
Werkdruk	5	19	11.85	2.79
Cognitieve werkeisen	33	97	72.96	12.95
Informatieverwerking	5	20	15.23	3.02
Probleemoplossing	6	20	14.20	3.17
Kennisvariatie	8	20	15.50	2.91
Taakcomplexiteit	6	20	14.42	3.55
Specialisatie	5	20	13.62	3.65
Tevredenheid	0	54	42.67	9.30
Tevredenheid3	0	157464	87022	38462
Taak/contextuele prestatie	29	65	47.52	7.17
Taakprestatie	12	25	18.14	3.09
Contextuele prestatie	15	40	29.38	5.65
Contraproductieve prestatie	5	20	11.92	3.94

 

7.1.3. Resultaten

Hieronder worden de resultaten per domein besproken. Alle relaties zijn 2-zijdig getoetst. Alle beschreven correlaties zijn ongecorrigeerde correlaties – er is dus geen correctie voor onbetrouwbaarheid van de criteriummaten toegepast.

7.1.3.1. Gezondheid

Rookgedrag

Een ANOVA-toets is uitgevoerd om het effect van ooit roken (nu of vroeger) op intelligentie te onderzoeken. Hoewel de verschillen niet significant waren, scoorden de personen die nu rookten of vroeger hadden gerookt lager dan de niet-rokers op zowel de Cijferreeksentest (F(1,90)= .01, p = .91), als de Figurenreeksen (F(1,90)= .27, p = .61) en Verbale Analogieën lager (F(1,90)= .18, p = .67). Hetzelfde gold voor de g-scores (F(1,90)= .12, p = .73).

Tabel 7.7. Scores op de ACT Algemene Intelligentie naar rookgedrag (N = 92).
	Ooit gerookt?
	Nee   (N = 38)		Ja   (N = 54)
	M	SD	M	SD	d
g-score	.25	.70	.20	.71	.07
Cijferreeksen	.17	.82	.15	.76	.02
Figurenreeksen	.14	.84	.05	.87	.11
Verbale Analogieën	.41	.82	.33	.92	.09

De categorische variabele bestaande uit drie categorieën (nee, af en toe, ja), liet geen significante verschillen in scores zien op de drie subtests en de g-scores – ook de effectgrootten waren te verwaarlozen.

Algehele gezondheid

De proefpersonen rapporteerden over het algemeen een redelijk goede gezondheid (M = 62.0, SD = 34.1, Min-Max. = 6-100). Er werd geen significante relatie gevonden tussen de scores op de ACT Algemene Intelligentie en algehele gezondheid (Tabel 7.8., onderste rij). De verdeling van de gezondheidsvariabele was bimodaal (feitelijk twee verdelingen; een bij lage scores en een bij hoge scores). Echter, de relaties tussen de ACT Algemene Intelligentie waren ook bij deze twee groepen afzonderlijk niet significant.

7.1.3.2. Sociaaleconomische status

Opleidingsniveau

Voor zowel de drie subtests als de g-score gold dat er significante verschillen in scores waren op basis van opleidingsniveau. Uit Figuur 7.2. blijkt dat deze verschillen precies volgens voorspelling zijn: hoe hoger het opleidingsniveau van een persoon, hoe hoger de scores op de ACT Algemene Intelligentie.

Figuur 7.2. Scores op de ACT Algemene Intelligentie naar opleidingsniveau (N = 92).

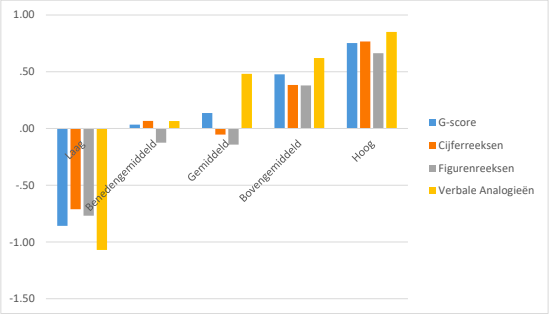
De effectgrootte op basis van η² is zeer groot te noemen (.405). Omgerekend naar een Pearsoncorrelatie komt dit overeen met r = .64; dit ligt dus nog wat hoger dan de waarde van .46 uit de meta-analyse van Strenze (2007).

Inkomen

In Figuur 7.3. zijn de gemiddelde ACT Algemene Intelligentie scores weergegeven per inkomensniveau. Ook hier is de voorspelde trend zichtbaar: mensen met een hoger inkomen scoren over het algemeen hoger op de ACT Algemene Intelligentie. Voor de g-score toonde een ANOVA-toets echter aan dat deze verschillen niet statistisch significant waren (F(5,78)= 1.20, p = .32), hoewel de effectgrootte η² een effect van gemiddelde grootte aangaf (η² = .071). Omgerekend naar een Pearson correlatie komt dit overeen met r = .27: dit is exact de waarde die we op basis van de meta-analyse van Ng et al. (2005) mogen verwachten.

Figuur 7.3. Scores op de ACT Algemene Intelligentie naar inkomen (N = 84).

 

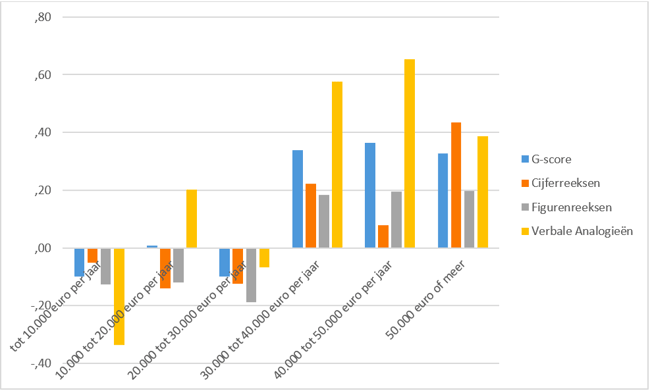
Beroep

In Figuur 7.4. zijn de gemiddelde scores weergegeven per beroepscategorie. De trend is zoals we voorspeld hadden: personen in lagere beroepscategorieën scoren lager op de ACT Algemene Intelligentie, en de scores worden hoger bij mensen uit hogere beroepscategorieën. De vierde beroepscategorie (N = 2) vertoonde een afwijkende score ten opzichte van deze trend. Maar over het algemeen kunnen we zeggen dat hogere intelligentie samen gaat met een hoger beroepsniveau, dat wil zeggen een hogere sociaaleconomische status.

Wanneer alle beroepscategorieën werden meegenomen was er alleen een marginaal significant verschil in scores bij Cijferreeksen (F(7,76)= 1.83, p = .09). Echter, wanneer we naar de effectgrootten η² kijken (in plaats van p-waarden) dan zien we dat de verschillen in scores tussen de beroepsniveaus als ‘gemiddeld’ (Figurenreeksen) of ‘groot’ (g-score, Cijferreeksen en Figurenreeksen) kunnen worden geclassificeerd (g-score = .141, CR = .144, FR = .076 en VA = .108)[1]. Voor de g-score betekent dit omgerekend naar een Pearson correlatie[2] een effect van r = .38. Dit komt bijna exact overeen met de resultaten uit de meta-analyse van Strenze uit 2007 (r = .37).

Figuur 7.4. Scores op de ACT Algemene Intelligentie naar beroep (8 categorieën; N = 84).

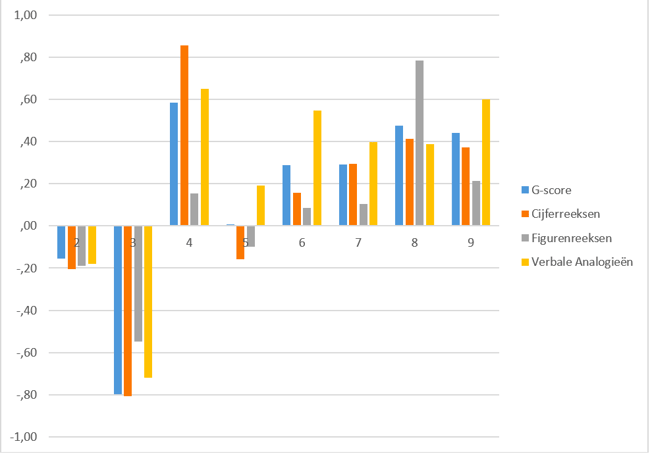
Wanneer we kijken naar de vijf beroepsniveaus (bestaande uit ongeveer gelijke aantallen), dan zien we dezelfde trend (Figuur 7.5.). Ondanks dat er geen significante verschillen gevonden zijn, waren de effectgrootten van gemiddelde grootte, wat indiceert dat er wel een positieve trend aanwezig is (g-score η² = .085, Cijferreeksen η² = .077, Figurenreeksen η² = .049 en Verbale Analogieën η² = .071). Voor de g-score betekent dit omgerekend naar een Pearson correlatie een effect van r = .29. Ook deze waarde komt in de buurt van de waarde die we op basis van meta-analyses mogen verwachten (r = .37).

Figuur 7.5. Scores op de ACT Algemene Intelligentie naar beroep (5 categorieën; N = 84).

 

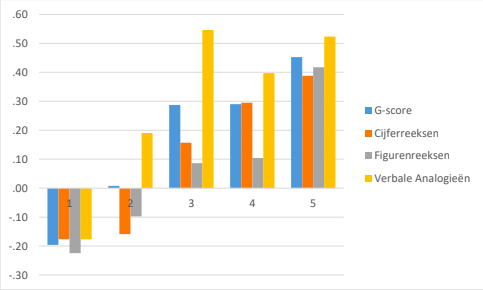
7.1.3.3. Relaties tussen intelligentie werkcomplexiteit en werktevredenheid

Hieronder worden de resultaten besproken van de toetsing van de hypothesen op basis van het onderzoek van Ganzach (1998).

Figuur 7.6. Gevonden relaties intelligentie (g-score ACT Algemene Intelligentie) en werkcomplexiteit en werktevredenheid (N = 84).

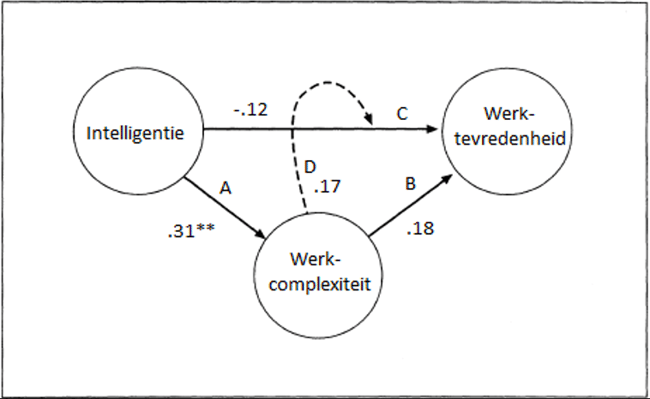
Tabel 7.8. Correlaties tussen variabelen criteriumstudie.
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
1.	g-score	1
2.	Cijferreeksen	.83**	1
3.	Figurenreeksen	.84**	.64**	1
4.	Verbale Analogieën	.90**	.58**	.63**	1
5.	Totale werkdruk	.10	.16	.04	.07	1
6.	Geestelijke belasting	.03	.11	-.05	.02	.90**	1
7.	Werkdruk	.17	.17	.16	.12	.82**	.50**	1
8.	Cognitieve werkeisen	.22*	.25*	.15	.18†	.64**	.61**	.48**	1
9.	Informatieverwerking	.10	.13	.10	.07	.72**	.70**	.52**	.85**	1
10.	Probleemoplossing	.08	.11	.00	.09	.37**	.29**	.36**	.71**	.55**	1
11.	Kennisvariatie	.26*	.31**	.18†	.21†	.49**	.47**	.37**	.91**	.73**	.64**	1
12.	Taakcomplexiteit	.31**	.29**	.24*	.27*	.48**	.44**	.38**	.76**	.58**	.30**	.66**	1
13.	Specialisatie	.10	.14	.06	.07	.50**	.54**	.31**	.77**	.56**	.39**	.63**	.45**	1
14.	Tevredenheid	-.01	.01	-.07	.02	.10	.19†	-.04	.36**	.31**	.35**	.46**	.18†	.17	1
15.	Tevredenheid3	-.06	-.02	-.11	-.05	.11	.17	.00	.36**	.32**	.37**	.43**	.15	.21†	.92**	1
16.	Taak/contextuele prestatie	.10	.06	-.06	.19†	.02	.09	-.08	.15	.17	.21†	.22*	-.10	.13	.43**	.35**	1
17.	Taakprestatie	.06	.01	-.03	.10	-.23*	-.10	-.33**	-.14	-.13	-.06	-.10	-.13	-.13	.25*	.18†	.66**	1
18.	Contextuele prestatie	.10	.06	-.06	.19†	.15	.17	.08	.27*	.28**	.30**	.33**	-.06	.24*	.41**	.35**	.91**	.29**	1
19.	Contraproductief werkgedrag	.09	.06	.12	.07	.07	.04	.09	-.18†	-.02	-.12	-.21†	-.28*	-.10	-.09	-.17	-.06	-.22*	.05	1
20.	Algehele gezondheida	.13	.12	.08	.11	-.11	-.08	-.11	-.12	-.21*	-.09	-.17	-.11	.06	-.04	.03	.02	.01	.02	.02
** p < .01 (2-zijdig),  * p < .05 (2-zijdig), † p < .10 (2-zijdig)
a N = 91, voor de rest van de variabelen geldt N = 84.

 

Intelligentie en complexiteit (Pad A)

Eerst hebben we gekeken naar de relaties tussen de verschillende cognitieve werkeisen en intelligentie. Over het algemeen vinden we, zoals voorspeld, positieve relaties tussen deze kenmerken van het werk en intelligentie (Tabel 7.8.). Deze relaties waren echter alleen significant voor scores op alle drie de subtests en de g-score voor taakcomplexiteit (r = .31) en kennisvariatie (r = .26). Met andere woorden, personen met hogere intelligentieniveaus doen werk dat uit meer complexe taken bestaat en waarbij men meer en verschillende kennis en vaardigheden bij nodig heeft. Interessant om op te merken is dat het effect van intelligentie op complexiteit overeenkomt met de studie van Ganzach (1998; r = .31, zie Figuur 7.1.).

Ook de correlatie tussen intelligentie en  de algehele maat voor cognitieve werkeisen was significant voor scores op Cijferreeksen (r = .25) en Verbale Analogieën (r = .18), en ook voor de g-score (r = .22). Dit betekent dat mensen met een hogere intelligentie over het algemeen werk doen waarbij meer van hen geëist wordt op cognitief vlak. Dit komt overeen met onze vooraf gestelde hypothese.

Intelligentie en werktevredenheid (Pad C)

Allereerst is het interessant op te merken dat de directe relatie tussen intelligentie en werktevredenheid niet significant is (r = -.06; zie Tabel 7.8., net als bij Ganzach, 1998). Dit geconstateerd hebbende toetsten we de hypothese dat, wanneer gecontroleerd wordt voor werkcomplexiteit, intelligentie een negatief effect heeft op werktevredenheid. Een regressieanalyse liet inderdaad een negatief effect zien van intelligentie (g-score) op tevredenheid onafhankelijk van complexiteit (β = -.12), hoewel dit effect niet significant was (p = .30). Dit zal echter vooral door de steekproefgrootte komen: het gevonden effect is namelijk vergelijkbaar met het effect gevonden door Ganzach (1998), die effecten van -.08 en -.11 vond (controlerend voor twee verschillende maten van complexiteit).

 Intelligentie en werktevredenheid, via werkcomplexiteit (Pad A + Pad B)

Vervolgens hebben we de mediatiehypothese getoetst. De gevonden effecten zijn weergegeven in Figuur 7.7., en zijn in lijn met de hypothesen van Ganzach (1998). Het indirecte effect van intelligentie op werktevredenheid via complexiteit (.31 * .18 = .06) was significant (p < .05): complexiteit medieert dus het effect van intelligentie op werktevredenheid. Intelligentere mensen lijken complexere banen te hebben, die hen meer tevredenheid en genoegdoening geven.

Wanneer we de getallen in Figuur 7.6. met die uit Figuur 7.1. vergelijken dan valt op dat de waarden sterk overeen komen met die van Ganzach (1998). De niet-significante relaties (bijvoorbeeld van complexiteit op tevredenheid, β = .18, p = .11) moeten dan ook vooral gezocht worden in het verschil in steekproefgrootte van onze studie ten opzichte van Ganzach. De verklaarde variantie (R²) in het model waarin tevredenheid voorspeld werd door complexiteit en intelligentie was 3%, evenveel als bij Ganzach.[3]

Moderatie van de intelligentie-werktevredenheid relatie door werkcomplexiteit (Pad D)

 Tot slot toetsten we de moderatiehypothese die stelde dat het negatieve effect van intelligentie op werktevredenheid minder sterk zou zijn voor complexere banen. Dit veronderstelt een positief interactie-effect tussen intelligentie en complexiteit op werktevredenheid. In een regressieanalyse werd dit positieve interactie-effect inderdaad gevonden (β = .17), hoewel niet significant (p = .13). Ook hier geldt weer voor dat het effect vergelijkbaar was met het effect gevonden door Ganzach (1998; β = .13). Het interactie-effect wordt grafisch weergegeven in Figuur 7.7.: zoals voorspeld is voor mensen die werken in banen met lage complexiteit het effect van intelligentie op tevredenheid negatief.[4] Echter, voor complexere banen geldt dat hoe intelligenter je bent, hoe meer tevreden je met je werk bent. Als je intelligenter bent zal je beter met de eisen die een complexere baan stelt om kunnen gaan en hier dus meer voldoening uit halen.

Het niet-significante directe effect van intelligentie op werktevredenheid is nu ook te verklaren op basis van de onderstaande figuur: als je een lijn trekt die precies in het midden van deze twee lijnen loopt dan is die ongeveer vlak, wat een nul-effect betekent.

Figuur 7.7. Interactie-effect van intelligentie en werkcomplexiteit op werktevredenheid (N = 84).

 

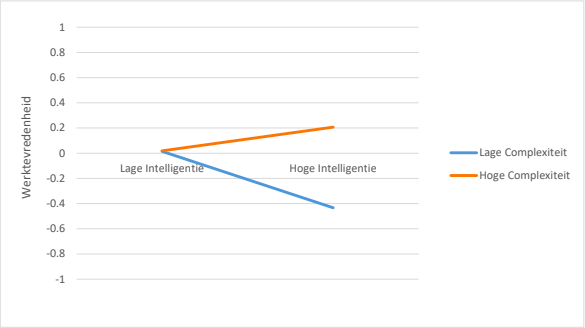
7.1.3.4. Werkprestatie

Uit Tabel 7.8. blijkt dat er geen directe relaties gevonden zijn tussen intelligentie gemeten door de ACT Algemene Intelligentie en werkprestatie. Toch hebben we getoetst of intelligentie een sterkere relatie met werkprestatie laat zien voor meer complexe banen – bovenstaande figuur geeft aan dat het mogelijk is een niet-significant direct effect te vinden terwijl er een interactie gaande is. Een regressieanalyse liet zien dat, hoewel niet significant bij een 2-zijdige toets, er inderdaad een positieve interactie is tussen intelligentie en complexiteit (β = .15, p = .20) wanneer taakprestatie als afhankelijke variabele werd genomen.[5] Dit interactie-effect is weergegeven in Figuur 7.8. Simple slope analyses toonden aan dat het effect van g op taakprestatie voor banen met lage complexiteit (complexiteit SD = -1) zo goed als nul was (B = .06, p = .88), terwijl het effect bij hoge complexiteit (complexiteit SD = +1) duidelijk positief was (B = .90, p = .11). Zoals voorspeld is het effect van intelligentie op taakprestatie dus sterker bij complexere banen dan bij banen met een lagere complexiteit. Sterker, het effect van intelligentie op taakprestatie is niet significant bij lage complexiteit (de blauwe lijn is bijna vlak) en significant positief bij hoge complexiteit.

Figuur 7.8. Interactie-effect van intelligentie en werkcomplexiteit op taakprestatie (N = 84).

 

 

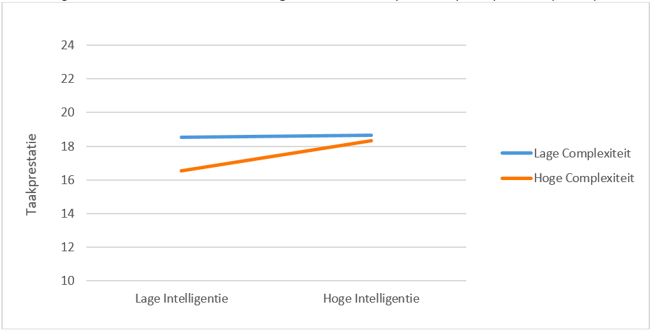
Additionele analyses: Relaties tussen werkprestatie controlerend voor werktevredenheid en werkeisen

Uit Tabel 7.8. blijkt dat werkprestatie samenhangt met werktevredenheid en met de werkeisen. Dit is ook wel te verwachten: het is aannemelijk dat iemand die zijn/haar werk helemaal niet leuk vindt, ook niet zijn/haar best zal doen en dus minder goed zal presteren (Judge, Thoresen, Bono, & Patton, 2001). Ook hangen werktevredenheid en werkeisen positief met elkaar samen: zoals verwacht vinden mensen die meer uitdagend werk doen hun werk ook leuker (Ganzach, 1998). Omdat intelligentie samenhangt met werkeisen, is het daarom interessant om te kijken naar de relaties tussen intelligentie en werkprestatie, wanneer gecontroleerd wordt voor werktevredenheid en werkeisen.

Om dit te onderzoeken is een regressieanalyse uitgevoerd waarbij werktevredenheid en werkeisen als controlevariabelen werden ingevoerd, naast de g-score uit de ACT Algemene Intelligentie. Deze regressieanalyse werd voor alle vier de prestatiematen gedaan (taak/contextuele prestatie, taakprestatie, contextuele prestatie en contraproductief werkgedrag). Voor de werkeisen-variabele werden afwisselend de maten voor totale werkeisen, taakcomplexiteit en kennisvariatie ingevoerd als controlevariabele (omdat deze significante relaties met de overige variabelen in het model vertoonden). In totaal werden er dus 12 (4×3) modellen getoetst. De resultaten uit deze analyses zijn weergegeven in Tabel 7.9.

Over het algemeen zien we, zoals verwacht, positieve effecten van intelligentie op taak- en contextuele prestatie en de somscore van deze twee prestatiematen. Deze effecten zijn echter niet significant verschillend van nul, met een enkele uitzondering. Zo bleek er een klein significant positief effect van intelligentie op taak/contextuele prestatie (β = .20, p = .07) en op contextuele prestatie (β = .18, p = .10) wanneer er gecontroleerd werd voor taakcomplexiteit en werktevredenheid. Onverwacht zijn de positieve effecten op contraproductief werkgedrag, hoewel ook deze effecten niet significant waren (zie Tabel 7.9., rechterkolommen).

 7.1.3.5. Schoolprestaties

Alle respondenten waren in de uitnodiging voor het onderzoek al gevraagd hun eindlijst van de middelbare school mee te nemen en dat ze hiervoor een extra vergoeding zouden ontvangen. Een aantal personen hadden dit gedaan, een aantal personen ook niet; in de instructie en in de debriefing werden zij eraan herinnerd dat zij dit alsnog konden doen.

In totaal hadden we van 42 personen informatie over de eindcijfers behaald op de middelbare school. Het gemiddelde cijfer was 6.68 (SD = .50, Min.  = 5.86, Max.  = 7.75). De correlaties tussen de g-score, Cijferreeksen, Figurenreeksen en Verbale Analogieën met het gemiddelde eindcijfer op de middelbare school waren respectievelijk .34 (p = .03), .44 (p = .00), .36 (p = .02) en .14 (p = .39). Mensen met hogere intelligentieniveaus blijken dus, zoals voorspeld, betere schoolprestaties te leveren dan mensen met lagere intelligentieniveaus. Deze resultaten zijn opvallend: voor sommige mensen was het wel decennia geleden dat de eindcijfers behaald werden. Toch blijken de scores op de ACT deze behaalde cijfers nog retrospectief te kunnen ‘voorspellen’.

Bovenstaande bivariate relaties zijn echter enigszins vertekend, omdat de personen in de steekproef middelbare scholen van verschillende niveaus hebben doorlopen. Daarom is er ook gekeken of de relatie tussen intelligentie zoals gemeten met de ACT Algemene Intelligentie nog steeds aanwezig was wanneer gecontroleerd werd voor schoolniveau. Dit is op twee manieren gedaan:

• van een deel van de personen die hun eindlijst hadden meegenomen (28 personen, 67%) was bekend op welk niveau deze eindcijfers waren behaald. Deze categoriale variabele is meegenomen (in de vorm van losse dummy-variabelen voor elk schoolniveau) als controlevariabele.
• de deelnemers vulden voor het maken van de tests informatie in over hun achtergrondkenmerken, waaronder over het hoogst behaalde opleidingsniveau (zie Tabel 6.20.). In een aparte analyse is deze categorische variabele meegenomen (in de vorm van losse dummy-variabelen voor elk opleidingsniveau) als controlevariabele.

Controleren voor het schoolniveau van het behaalde diploma (Manier 1) had weinig tot geen effect op de relaties tussen de scores op de verschillende tests en het behaalde eindcijfer: g-score (β = .34, p = .10), Cijferreeksen (β = .38, p = .07), Figurenreeksen (β = .39, p = .04) en Verbale Analogieën (β = .17, p = .41).

Echter, controleren voor het uiteindelijk behaalde opleidingsniveau van de deelnemer (Manier 2) zorgde ervoor dat de effecten van intelligentie op de behaalde eindcijfers verdwenen: g-score (β = .06, p = .74), Cijferreeksen (β = .21, p = .25), Figurenreeksen (β = .19, p = .33) en Verbale Analogieën (β = -.06, p = .68).

Bij de tweede manier van controleren zijn de resultaten op meerdere personen gebaseerd (omdat we meer informatie hadden over het uiteindelijk behaalde opleidingsniveau dan het niveau waarop het diploma behaald was). Echter, bij de eerste manier zijn de uitkomstmaat (behaalde cijfers) en de controlevariabele (het niveau waarop deze cijfers behaald zijn) theoretisch en praktisch meer aan elkaar verwant: het uiteindelijk behaalde opleidingsniveau kan door een zeer groot aantal overige factoren beïnvloed zijn. Het is dus lastig in te schatten wat precies de betere manier is. We kunnen in ieder geval concluderen dat er een positieve relatie tussen scores op de ACT Algemene Intelligentie en behaalde eindcijfers op de middelbare school aanwezig is, maar dat het onduidelijk is in hoeverre deze relatie verklaard wordt door het schoolniveau.

7.1.4. Conclusies met betrekking tot criteriumvaliditeitsonderzoek

In dit onderzoek zijn de relaties tussen de ACT Algemene Intelligentie en verschillende criteriummaten onderzocht. Hieronder worden de bevindingen kort samengevat en geduid.

Scores op de ACT lieten nauwelijks relaties zien met uitkomsten gerelateerd aan gezondheid. Een verklaring hiervoor zou het cross-sectionele karakter van de studie kunnen zijn: de meeste studies naar intelligentie en gezondheid zoeken naar relaties tussen IQ op een jonge leeftijd en gezondheid(sproblemen) op latere leeftijd (Gottfredson & Deary, 2004). Ook is bekend dat zeer veel verschillende factoren van invloed zijn op gezondheid (bijvoorbeeld sociale klasse of woonplek/geografische locatie; Gottfredson, 2004)  – het niet meenemen van deze variabelen kan er ook voor gezorgd hebben dat we geen relaties hebben gevonden. Een andere verklaring voor de niet gevonden relatie tussen algehele gezondheid en de ACT Algemene Intelligentie is het feit dat gezondheid slechts met één item gemeten werd. Gezien het gebruiksdoel van de ACT Algemene Intelligentie is het feit dat we weinig relaties met gezondheid vonden minder van belang. De ACT Algemene Intelligentie is met name bedoeld voor selectiedoeleinden en om dus de beste kandidaten te selecteren: het aantonen van relaties met werkgerelateerde uitkomsten of school- en studie uitkomsten (die gezien kunnen worden als een indicatie van later werkgedrag) is in dit opzicht relevanter.

Hoewel niet altijd significant, vonden we duidelijke relaties tussen de ACT Algemene Intelligentie en indicatoren van sociaaleconomische status zoals beroepsniveau, inkomen en opleidingsniveau. Opvallend was dat bij beroepsniveau en inkomen de gevonden effecten bijna identiek waren aan de gevonden effecten in de betreffende meta-analyses: verschillen in scores op de ACT Algemene Intelligentie lijken dus samen te gaan met deze reële verschillen tussen groepen. Dit biedt sterke ondersteuning voor de criteriumvaliditeit van de test.

De ACT Algemene Intelligentie vertoonde ook een aantal belangrijke relaties met  werkgerelateerde uitkomstmaten. Zo vonden we voorspelde relaties tussen intelligentie en complexiteit van het werk. Analyses toonden verder aan dat meer complexe hypothesen zoals die over de relaties tussen intelligentie, werktevredenheid en werkcomplexiteit ook bevestigd konden worden. Het feit dat relaties die we op basis van eerder onderzoek kunnen verwachten ook met behulp van de ACT Algemene Intelligentie gevonden worden biedt ondersteuning voor de criteriumvaliditeit van deze test.

Er werd geen directe relatie gevonden tussen intelligentie en werkprestatie. Echter, wanneer gecontroleerd werd voor werktevredenheid en kenmerken van het werk, dan werd wel een effect van intelligentie gevonden op werkprestatie (taak- en contextuele prestatie gecombineerd). Ook vonden we een indicatie dat het effect van intelligentie op taakprestatie sterker was bij complexere banen dan bij banen met een lagere complexiteit. Een mogelijke reden voor het niet vinden van een directe relatie tussen intelligentie en werkprestatie kan dan ook het heterogene karakter van de steekproef zijn: verschillen in zowel intelligentie als werkprestatie tussen beroepsgroepen kunnen, wanneer bij elkaar geveegd in één studie, deze relaties vertroebelen (Dilchert, Ones, Davis, & Rostow, 2007). Het is daarom wenselijk om in de toekomst binnen een bepaalde beroepsgroep de relatie tussen intelligentie zoals gemeten met  de ACT Algemene Intelligentie en  werkprestatie te onderzoeken.

Tot slot  kunnen we stellen dat de relatief sterke relatie die we vonden (r = .34 voor de g-score) tussen intelligentie en schoolprestaties zeer goede ondersteuning bieden voor de criteriumvaliditeit van de ACT Algemene Intelligentie. Zoals gezegd was het voor sommige mensen wel decennia geleden dat de eindcijfers behaald werden. Toch bleken de scores op de ACT Algemene Intelligentie deze behaalde cijfers nog retrospectief te kunnen ‘voorspellen’. Het feit dat deze relaties standhouden ondanks dit gat in de tijd geeft aan dat de ACT Algemene Intelligentie goed gebruikt kan worden om uitkomsten in de echte wereld – zoals schoolprestaties – te kunnen voorspellen.

Tabel 7.9. Resultaten regressieanalyse naar de voorspelling van werkprestatie (N = 84).
	Taak/contextuele prestatie					Taakprestatie					Contextuele prestatie					Contraproductief werkgedrag
	B	SE	β	p	R2	B	SE	β	p	R2	B	SE	β	p	R2	B	SE	β	p	R2
Constante	41.77	4.31		.00		20.76	1.90		.00		21.01	3.37		.00		16.46	2.48		.00
g-score	1.33	1.09	.13	.23		.59	.48	.13	.22		.74	.86	.09	.39		.66	.63	.12	.29
Werkeisen	-.01	.06	-.01	.92		-.07	.03	-.28	.02		.06	.05	.14	.24		-.05	.04	-.17	.16
Tevredenheid3	.00	.00	.37	.00		.00	.00	.29	.01		.00	.00	.31	.01		.00	.00	-.10	.40
R2					.14**					.10*					.15**					.06
Constante	47.06	3.32		.00		19.04	1.52		.00		28.01	2.65		.00		17.76	1.89		.00
g-score	2.01	1.09	.20	.07		.59	.50	.13	.24		1.42	.87	.18	.10		1.00	.62	.18	.11
Taakcomplexiteit	-.45	.22	-.22	.04		-.18	.10	-.21	.08		-.27	.17	-.17	.13		-.35	.12	-.32	.01
Tevredenheid3	.00	.00	.40	.00		.00	.00	.22	.04		.00	.00	.39	.00		.00	.00	-.11	.29
R2					.19**					.08†					.16**					.12*
Constante	40.10	4.12		.00		20.23	1.82		.00		19.87	3.20		.00		16.83	2.36		.00
g-score	1.17	1.12	.12	.30		.64	.49	.15	.20		.53	.87	.07	.54		.78	.64	.14	.22
Kennisvariatie	.10	.30	.04	.73		-.28	.13	-.27	.04		.39	.23	.20	.10		-.29	.17	-.21	.10
Tevredenheid3	.00	.00	.34	.00		.00	.00	.31	.01		.00	.00	.27	.02		.00	.00	-.07	.57
R2					.14**					.09†					.17**					.07

7.2. Onderzoek naar het effect van intelligentie en divergent denken op academische prestaties

7.2.1. Introductie

Verschillen tussen studenten in academische prestaties worden door meerdere factoren veroorzaakt. Intelligentie is de meest erkende voorspeller voor prestatie op school en tijdens de studie (Chamorro-Premuzic & Furnham, 2008). Intelligentie lijkt echter ongeveer 25% van de variantie in prestaties te voorspellen, wat ruimte over laat voor andere predictoren. Eén van deze mogelijke voorspellers is creativiteit (zie bijvoorbeeld Ai, 1999).

Creativiteit is een breed construct. Met creativiteit wordt het proces bedoeld waarin een individu nieuwe en originele producten of ideeën bedenkt (Batey & Furnham, 2006). Verder zijn de vaardigheden die relevant zijn voor creatief denken verdeeld in twee categorieën: divergent denken en convergent denken (Guilford, 1967). Met divergent denken zijn er meerdere antwoorden mogelijk voor een gesteld probleem of opgave en is het van belang zo veel mogelijke oplossingen te bedenken. Hierbij wordt onderscheid gemaakt tussen fluency (het aantal ideeën), flexibiliteit (het aantal categorieën) en de originaliteit van de oplossing (Batey & Furnham, 2006). Bij convergent denken is er echter maar één antwoord de juiste oplossing.

Er is herhaaldelijk aangetoond dat intelligentie en divergent denken relatief sterk met elkaar samenhangen (Hocevar, 1980; Batey, Chamorro-Premuzic, & Furnham, 2009; Getzels & Jackson, 1962; Vincent, Decker, & Mumford, 2002). Tegelijkertijd lijkt divergent denken te zijn gerelateerd aan academische prestaties (Ai, 1999; Runco & Albert, 1985; Shin & Jacobs, 1973). Op basis van het bovenstaande kunnen we dus ook een positieve relatie verwachten tussen intelligentiescores op basis van de ACT Algemene Intelligentie en (1) academische prestaties en (2) scores op divergent denken-taken.

Intelligentie en divergent denken lijken beiden academische prestaties te voorspellen, en tegelijkertijd onderling samen te hangen. Een meta-analyse van Kim (2008) liet zien dat de relatie tussen divergent denken en creatieve prestaties (r = .22) ongeveer even sterk – zelfs nog iets sterker – is dan de relatie tussen intelligentie en creatieve prestaties (r = .17). Hieruit trok Kim (2008) de conclusie dat divergent denken een betere voorspeller is voor creatieve prestaties dan intelligentie. Vincent et al. (2002) toonden verder aan dat divergent denken unieke variantie verklaarde (los van intelligentie) in creatief oplossingsvermogen. Omdat wordt verwacht dat creativiteit academische prestaties voorspelt, wordt de rol van divergent denken bij het voorspellen van academische prestatie interessant.

Intelligentie wordt zoals hierboven beschreven traditioneel gezien als de sterkste voorspeller van academische prestatie (Von Stumm et al., 2011), maar het is interessant om te onderzoeken of een deel van de variantie niet verklaard wordt door divergent denken. In dit onderzoek wordt daarom de voorspellende waarde van intelligentie op academische prestatie bekeken, terwijl ook de voorspellende waarde van divergent denken op academische prestatie wordt beoordeeld. De verwachting is dat zowel intelligentie als divergent denken academische prestatie voorspellen.

Ten slotte wordt onderzocht of divergent denken bovenop intelligentie effect heeft op academische prestatie. Dat wil zeggen; of divergent denken nog steeds voorspellend is voor academische prestaties als er ook rekening wordt gehouden met de intelligentie van de persoon. Gebaseerd op de resultaten van Kim (2005; 2008) en Vincent et al. (2002) wordt verwacht dat divergent denken bovenop het effect van intelligentie op academische prestatie, extra variantie verklaart – en andersom.

 7.2.2. Methode

7.2.2.1. Steekproef

Aan dit onderzoek hebben in eerste instantie totaal 115 personen zich ingeschreven. Alle deelnemers waren verbonden als student aan een grote universiteit in Nederland. Er waren geen restricties verbonden aan deelname aan dit onderzoek, mits de proefpersonen niet eerder deel hadden genomen aan een soortgelijk onderzoek. Alleen volledige data zijn meegenomen in de analyse, waardoor de data van 66 proefpersonen bruikbaar was. Deze deelnemers bestonden uit 14 mannen (21%) en 52 vrouwen (79%). Deze deelnemers hadden een leeftijd variërend tussen 18 en 25 jaar. De gemiddelde leeftijd was 20.3 (SD = 1.78). De data van dit onderzoek zijn verzameld tussen 3 maart 2016 en 22 april 2016. Alle proefpersonen hebben één proefpersoonuur gekregen voor deelname aan het onderzoek.

7.2.2.2. Instrumenten

Academische prestatie

De academische prestaties van de proefpersoon is gemeten door naar het gemiddelde cijfer van de proefpersoon te vragen. Dit is het gemiddelde cijfer dat is behaald bij de tentamens behorende bij de studie.

 Intelligentie

 Intelligentie is gemeten aan de hand van de ACT Algemene Intelligentie. De betrouwbaarheden op basis van de SEM methode (1 – SEM²) waren .87, .83 en .91 voor respectievelijk Cijferreeksen, Figurenreeksen en Verbale Analogieën. Cronbach’s alfa van de g-score was slechts .63 in de huidige steekproef, de empirische betrouwbaarheid (zie Hoofdstuk 5) was echter .88.

Divergent Denken

 Guilford’s Alternate Uses Task

 Divergent denken is gemeten door gebruik te maken van een zogenaamde Alternate Uses Task (AUT). Bij een AUT dient de deelnemer zoveel mogelijk manieren te verzinnen voor het gebruik van een bepaald voorwerp – in het huidige onderzoek een paperclip (Guilford, 1967). De creativiteit van de deelnemer wordt vervolgens bepaald aan de hand van een productiescore en een originaliteitsscore. De hoeveelheid serieuze verzonnen manieren worden bij elkaar opgeteld wat zorgt voor een productiescore. Alle antwoorden worden in categorieën verdeeld zodat vergelijkbare antwoorden in dezelfde categorie worden geplaatst. De antwoorden die drie keer of minder zijn genoemd door alle kandidaten krijgen een score van twee punten en de antwoorden die vier tot acht keer zijn genoemd scoren één punt. De originaliteitspunten van de antwoorden van de deelnemer worden bij elkaar opgeteld, wat per persoon een totale originaliteitsscore oplevert. Hocevar (1980) berekende de betrouwbaarheid van de AUT en vond in zijn onderzoek een Chronbach’s alfa van .89 voor mannen en .87 voor vrouwen, wat betekent dat de AUT een betrouwbare divergent denken test is.

Divergent Denken Test

Omdat het automatisch scoren van taken als de AUT moeilijk is en de scoringsprocedure kritiek ontvangen heeft (zie bijvoorbeeld Benedek, Mühlmann, Jauk, & Neubauer, 2013), is de DDT ontworpen (Van Zand et al., 2015). De DDT is een figuratieve test, bestaand uit zes items met elk een figuur met negen vakken (zie Figuur 7.9.). Elk vak bevat één of meerdere figuren. Met deze figuren maakt de deelnemer combinaties van drie vakken, door overeenkomsten aan te geven die de overige zes vakken niet hebben. De hoeveelheid combinaties die de deelnemer maakt, is de productiescore op de DDT. Hoe origineel deze antwoorden zijn hangt af van hoe vaak deze antwoorden in totaal zijn gegeven door alle deelnemers. De originaliteitsscore is berekend door per item te kijken naar de decielen van de gegeven antwoorden. Dat betekent dat hoe vaker een antwoord is genoemd door de deelnemers, dit een lager originaliteitsscore per antwoord oplevert. Een antwoord binnen het eerste deciel en een antwoord binnen het vierde deciel krijgen een originaliteitsscore van respectievelijk tien en zeven punten. De originaliteitsscore van een persoon is de originaliteitsscore op alle door die persoon gegeven antwoorden bij elkaar opgeteld. De productiescore en originaliteitsscore hebben een Cronbach’s alfa van respectievelijk .84 en .76 in het huidige onderzoek.

 Figuur 7.9. Voorbeelditem van de Divergent Denken Test.

7.2.2.3. Procedure

Deelnemers konden zich online inschrijven voor dit onderzoek op de onderzoekpagina van een grote universiteit in Nederland. Bij inschrijving ontvingen de deelnemers een email van de proefleiders met daarin een aantal vragenlijsten. Allereerst dienden deelnemers antwoord te geven op vragen over hun achtergrond, vervolgens werd de vraag gesteld over hun gemiddeld tentamencijfer, waarna de AUT werd voltooid. Bij de AUT kregen de deelnemers 15 minuten de tijd om zoveel mogelijk manieren te verzinnen voor het gebruik van een paperclip, maar werd de mogelijkheid geboden deze test eerder af te breken. ‘Het bij elkaar houden van papier’ werd als voorbeeld gegeven voor aanvang van de test. Bij het volbrengen van alle tests, kregen de deelnemers toegang tot het maken van de ACT en de DDT. Ook deze tests zijn per mail naar de proefpersonen gestuurd door de proefleiders.

In het huidige onderzoek zijn de tests die de variabelen voorspellen (creativiteit, divergent denken en intelligentie) met elkaar gecorreleerd om de samenhang te controleren. De verwachting dat intelligentie gerelateerd is aan divergent denken wordt bevestigd zodra er een positieve correlatie wordt gevonden tussen de ACT en respectievelijk de DDT en AUT.

Bij correlaties wordt er uitsluitend gekeken naar relaties tussen variabelen onderling. Echter, in het huidige onderzoek is van belang wat de voorspellende waarde is van bijvoorbeeld divergent denken op academische prestaties, bovenop de voorspellende waarde van intelligentie op academische prestatie. Om te bepalen of intelligentie samen met creativiteit/divergent denken academische prestatie beter voorspelt dan alleen intelligentie, is een aantal hiërarchische regressieanalyses uitgevoerd. Bij een hiërarchische regressieanalyse worden meerdere modellen met elkaar vergeleken op het gebied van verklaarde variantie.

De bijdrage van de variabelen in het voorspellen van academische prestatie werd bepaald door model 1 (intelligentie) te vergelijken met model 2 (intelligentie en divergent denken). Verder werd een hiërarchische regressieanalyse worden uitgevoerd waarbij model 1 (divergent denken) werd vergeleken met model 2 (divergent denken en intelligentie). Voor bovenstaande modellen gold dat divergent denken steeds werd gemeten door de AUT of door DDT. Op basis van deze analyses kan dus bepaald worden in hoeverre intelligentie voorspellende waarde heeft bovenop het effect van divergent denken, en andersom.

Het vergelijken van de modellen ging in termen van verklaarde variantie. De proportie verklaarde variantie wordt weergeven in R². Bij een significante toename in verklaarde variantie van model 1 naar model 2 kunnen we spreken van incrementele validiteit van de in model 2 toegevoegde variabelen in de voorspelling van academische prestaties.

7.2.3. Resultaten

De gemiddelde scores en standaarddeviaties op de tests zijn weergegeven in Tabel 7.10. De spreiding van divergent denken geoperationaliseerd door originaliteit op de AUT (SD = 1.23) was groter dan het gemiddelde (M = .89). Dit betekent dat veel deelnemers een originaliteitsscore hadden van 0, maar dat uitschieters ervoor hebben gezorgd dat het gemiddelde hoger was. De scores op de AUT zijn scheef naar rechts verdeeld. Ook valt een hoge spreiding op bij divergent denken, geoperationaliseerd door de originaliteitsscore op de DDT (SD = 30.29), vergeleken met het gemiddelde (M = 53.97). Er lijkt dus veel verschil te zitten in originaliteit bij de deelnemers. De scores op de DDT zijn, tegenstelling tot de AUT, normaal verdeeld. Zoals we mogen verwachten bij academische studenten zijn de gemiddelde scores op de ACT Algemene Intelligentie relatief hoog (ongeveer IQ = 110).

Tabel 7.10. Beschrijvende statistieken (N = 66).
	Min.	Max.	Gem.	SD
g-score	-1.13	1.64	.63	.58
Cijferreeksen	-1.18	2.05	.55	.64
Figurenreeksen	-1.82	2.08	.58	.88
Verbale Analogieën	-1.28	2.24	.76	.74
DD: Guilford productie	4	24	9.77	4.33
DD: Guilford originaliteit	0	4	.89	1.23
DD: DDT productie	4	44	22.03	9.93
DD: DDT originaliteit	10	133	53.97	30.29
DD: DDT productie/originaliteit	1.57	3.75	2.38	.52
Academische prestaties	4.10	9.00	6.77	.92

In Tabel 7.11. zijn de correlaties tussen de verschillende constructen weergegeven.

Tabel 7.11. Correlaties tussen onderzoeksvariabelen
		1	2	3	4	5	6	7	8	9	10
1	g-score	.63/.88
2	Cijferreeksen	.64**	..87
3	Figurenreeksen	.74**	.34**	.83
4	Verbale Analogieën	.85**	.29*	.45**	.91
5	DD: Guilford productie	-.01	.15	.04	-.14	–
6	DD: Guilford originaliteit	-.02	.03	-.06	.00	.57**	–
7	DD: DDT productie	.38**	.36**	.32**	.25*	.37**	.20†	.84
8	DD: DDT originaliteit	.38**	.35**	.33**	.26*	.38**	.22†	.94**	.76
9	DD: DDT productie/originaliteit	.06	.07	.10	.03	.13	.06	.28*	.55**	–
10	Academische prestatie	.37**	.25*	.26*	.33**	.19	.02	.42**	.38**	-.02	–
** p < .01 (2-zijdig) * p < .05 (2-zijdig) † p < .10 (2-zijdig)
Noot. Betrouwbaarheden, wanneer van toepassing, op de diagonaal. Voor de G-score α/empirische betrouwbaarheid. Voor de drie subtests zijn dit 1 – SEM2.

Er bleek, zoals verwacht, een positief en significant verband tussen intelligentie en divergent denken, wanneer geoperationaliseerd als de productie- en originaliteitsscore van DDT, beiden r = .38, p < .01. Dat betekent dat mensen die hoog scoren op intelligentie hoog scoren op zowel het productie- als originaliteitsaspect van divergent denken. Hierbij moet echter opgemerkt worden dat deze twee maten van divergent denken nauwelijks van elkaar te onderscheiden zijn, wat geconcludeerd kan worden op basis van de hoge onderlinge correlatie (r = .94). De mate van originaliteit was dus altijd hoger wanneer veel combinaties werden gevonden. De hoge correlatie komt door het feit dat wanneer een persoon meer antwoorden geeft dan anderen, dit altijd zorgt dat de originaliteitsscore van deze persoon stijgt. De DDT-score waarbij de originaliteitsscore gecorrigeerd wordt voor de productiescore laat geen enkele significante correlatie met de andere variabelen zien.

Ook  de relatie tussen de productiescore en originaliteitscore van de AUT was positief (r = .57, p < .01). Dat betekent ook hier weer dat wanneer een persoon veel manieren wist te verzinnen voor het gebruik van een paperclip, ook de mate van originaliteit van de gegeven antwoorden over het algemeen hoger is. Verder correleerde de productiescore van de AUT met zowel de productiescore als de originaliteitsscore van de DDT. Voor de productiescore van de DDT was dit r = . 37, p < .01, en voor de originaliteitsscore r = .38, p < .01. Dat houdt in dat wanneer iemand veel manieren weet te verzinnen voor het gebruik van een paperclip, over het algemeen ook meer en originelere antwoorden geeft op de DDT.

De belangrijkste hypothese, in het kader van predictieve validiteit van de ACT Algemene Intelligentie, was de positieve relatie tussen intelligentie en academische prestaties. Zoals verwacht liet intelligentie een significant en positief verband zien met academische prestaties, r = .37, p < .01.

Interessant is ook dat, volgens verwachting, het gemiddelde tentamencijfer positief met de productiescore van de DDT samenhing, r = .42, p < .01. Daarnaast had het tentamencijfer een positieve correlatie met de originaliteitsscore van de DDT, r = .38, p < .01. De sterkte van het effect – nog sterker dan intelligentie – is opvallend en hoger dan we op basis van de literatuur mogen verwachten (Kim, 2008). Personen die in staat zijn meer divergent te denken lijken dus ook betere academische prestaties te leveren. Opvallend is dat divergent denken, gemeten door de AUT, niet positief correleerde met academische prestaties, terwijl divergent denken, gemeten door de DDT, dit wel deed.

Regressieanalyses

Tabel 7.12. geeft de resultaten weer van de analyse waarin wordt gekeken of divergent denken bovenop intelligentie extra variantie verklaart in academische prestaties. Omdat de AUT geen significante relaties liet zien met academische prestaties zijn deze analyses alleen voor de DDT uitgevoerd. Divergent denken, gemeten door DDT, verklaarde extra variantie bovenop intelligentie, originaliteit F(1,63) = 5.46, p = .02, R² = .21; productie F(1,63) = 7.52, p = .01, R² = .23. Het verschil in R²  was dus significant tussen de modellen, ∆R² = .07 (originaliteit) en ∆R² = .09 (productie). De voorspelling van academische prestaties werd dus beter (7% en 9% beter) wanneer divergent denken toegevoegd werd als voorspeller, naast intelligentie.

Tabel 7.12. Resultaten hiërarchische regressieanalyses incrementele validiteit divergent denken.
		Academische prestaties
		Model 1			Model 2a			Model 2b
		B	SE B	β	B	SE B	β	B	SE B	β
Constante		6.40**	.16		5.85**	.25		6.04**	.22
Intelligentie		.59**	.19	.37	.39*	.19	.25	.42*	.19	.26
DD	DDT productie				.03**	.01	.33
	DDT originaliteit							.01*	.00	.28
R2		.14**			.23**			.21**
F		10.20**			9.38**			8.19**
∆R2					.09**			.07*
Noot. N = 66. ∆R2 = de verandering van de verklaarde variantie van Model 1 ten opzichte van Model 2.   ** p < .01 (2-zijdig), * p < .05 (2-zijdig)

Tabel 7.13. geeft de resultaten weer van de analyse waarin wordt gekeken of intelligentie bovenop divergent denken extra variantie verklaart in academische prestaties. Intelligentie voorspelde bovenop divergent denken, gemeten door DDT, extra variantie, F(1,63) = 4.69, p = .03, R² = .21 (originaliteit) en F(1,63) = 4.25, p = .04, R² = .23 (productie). De toename in de verklaarde variantie van academische prestaties na toevoeging van intelligentie aan het model was dus significant, ∆R² = .06 (originaliteit) en ∆R² = .05 (productie). De voorspelling van academische prestaties werd dus beter (met 6% en 5%) wanneer intelligentie toegevoegd werd als voorspeller, naast divergent denken. Het is dus interessant om op te merken dat, hoewel het elkaar niet erg ontloopt, de incrementele validiteit van divergent denken over intelligentie groter is dan andersom.

Tabel 7.13. Resultaten hiërarchische regressieanalyses incrementele validiteit intelligentie.

Academische prestaties

Model 1a

Model 2a

Model 1b

Model 2b

B

SE B

β

B

SE B

β

B

SE B

β

B

SE B

β

Constante

5.91**

.25

5.85**

.25

6.14**

.22

6.04**

.22

DD

DDT productie

.04**

.01

.42

.03**

.01

.33

DDT originaliteit

.01**

.00

.38

.01*

.00

.28

Intelligentie

.39*

.19

.25

.42*

.19

.26

R2

.18**

.23**

.15**

.21**

F

13.81**

9.38**

11.05**

8.19**

∆R2

.05*

.06*

Noot. N = 66. ∆R2 = de verandering van de verklaarde variantie van Model 1 ten opzichte van Model 2.   ** p < .01 (2-zijdig), * p < .05 (2-zijdig)

 

7.2.4. Conclusie en discussie

In deze studie is aangetoond dat de ACT Algemene Intelligentie sterk samenhangt met, zoals verwacht op basis van eerdere literatuur, divergent denken, en belangrijker, academische prestaties. Wat betreft de sterkte van het gevonden effect op academische prestaties (r = .37), dan ligt deze redelijk in lijn met de gevonden effecten in de literatuur (uiteenlopend tussen de .30 en .70, met een verwachte waarde van .50, Roth et al., 2015). Ook de relatie met divergent denken is conform de literatuur, hoewel anderen nog wat hogere waarden vinden.[6] Hiermee draagt dit onderzoek verder bij aan de criteriumvaliditeit van de ACT Algemene Intelligentie.

[1] Afgezet tegen de richtlijnen van Cohen (1988): .01 is een klein effect, .06 gemiddeld en .14 is een groot effect.

[2] Hiervoor is gebruik gemaakt van de spreadsheet van Jamie DeCoster via http://www.stat-help.com/spreadsheets.html.

[3] Dit was het geval voor één van de twee complexiteitsmaten die gebruikt werden, voor de andere maat was dit 18%.

[4] Simple slope analyses toonden aan dat beide regressielijnen niet significant verschilden van 0. Dit zal voornamelijk te wijten zijn aan de kleine steekproefgrootte – en daarmee het gebrek aan power.

[5] Wanneer de andere prestatiematen als afhankelijke variabelen werden genomen waren de interactie-effecten te verwaarlozen. Hetzelfde gold voor wanneer de andere maten van werkeisen als moderator werden genomen. Dit was overigens ook het geval bij de mediatiehypothesen.

[6] Dit is gerelateerd aan de discussie in hoeverre divergent denken niet een onderdeel van intelligentie is (Nusbaum & Silvie, 2011), om eenvoudigheidsredenen hebben we deze discussie hier vermeden.