Handleiding Adaptieve Persoonlijkheid Vragenlijst
De Adaptieve Persoonlijkheid Vragenlijst (APV) is een adaptieve versie van de Werkgerelateerde Persoonlijkheid Vragenlijst (WPV), een vragenlijst die werkgerelateerde persoonlijkheid meet.
Leeswijzer Adaptieve Persoonlijkheid Vragenlijst
Voor uw gemak hebben wij een leeswijzer opgesteld. Deze leeswijzer geeft een korte beschrijving en daarbij de belangrijkste conclusies van elk hoofdstuk. Zo krijgt u eenvoudig en snel inzicht in de informatie die relevant is voor het gebruik van de Adaptieve Persoonlijkheid Vragenlijst (APV).
Bij een adaptieve vragenlijst krijgt niet iedere kandidaat exact dezelfde lijst met vragen. Enkel de vragen die aanvullende informatie opleveren over de persoonlijkheid van de kandidaat worden gesteld. Welke vragen gesteld worden, is afhankelijk van de antwoorden die de kandidaat heeft gegeven op eerder gestelde vragen. In de praktijk betekent dit dat vrijwel iedere kandidaat een andere vragenlijst krijgt. Als alle eigenschappen van de kandidaat betrouwbaar genoeg zijn gemeten, stopt de vragenlijst. De APV zorgt er dus voor dat kandidaten geen vragen krijgen die voor hen niet van toepassing zijn. Dit maakt de vragenlijst korter en minder herhalend, en daarmee minder belastend voor de kandidaat. In de volgende hoofdstukken geven we een toelichting over de ontwikkeling van de vragenlijst en presenteren we het onderzoek dat gedaan is naar deze vragenlijst.
1. Uitgangspunten bij de testconstructie
Voor de ontwikkeling van de adaptieve vragenlijst hebben we op basis van uitgebreid onderzoek per vraag vastgesteld welke informatie deze vraag oplevert voor verschillende persoonskenmerken. Simpel gezegd selecteert het systeem uit een grote bak met vragen steeds de vraag, die na de vorige vraag, de meeste informatie oplevert. Dit gaat door totdat alle schalen voldoende nauwkeurig gemeten zijn. In dit hoofdstuk gaan we in op de voordelen van adaptief testen, gemiddeld levert de adaptieve wijze van bevragen al na 92 vragen voldoende informatie op om betrouwbare uitspraken te doen over de persoonlijkheid van de kandidaat. In de praktijk betekent dit dat kandidaten een veel prettigere ervaring hebben bij het maken van de vragenlijst. Zij komen nauwelijks ‘dubbele’ items die naar dezelfde kenmerken vragen tegen en zijn 3 keer sneller klaar met het invullen van de vragenlijst. Verder leest u in dit hoofdstuk meer over de multidimensionale itemrespons theorie, het statistische model dat gebruikt wordt bij adaptieve tests. Hierbij staan we ook uitgebreid stil bij de gemaakte keuzes bij en onderzoeken naar de itempool, de methode van itemselectie, de startregel en de stopregel van de adaptieve test.
De vragenlijst is gebaseerd op de ‘Big Five’ persoonlijkheidstheorie, en bevat dezelfde items als de grondig gevalideerde en door de COTAN positief beoordeelde Werkgerelateerde Persoonlijkheid Vragenlijst (zie ook de handleiding van de WPV). Er wordt een uitslag gegeven op 5 factoren en 25 schalen. Deze 5 factoren zijn:

2. Betrouwbaarheid en validiteit
Uit onderzoek blijkt dat de betrouwbaarheden van de APV zeer hoog zijn (gemiddeld .87 voor de schalen en .95 voor de factoren). Daarnaast tonen analyses aan dat de uitslagen van de APV en de klassieke WPV sterk met elkaar samenhangen. Uit onderzoek blijkt dat de correlaties tussen de APV en WPV zeer hoog zijn (gemiddelde r = .92). en dat de factorstructuur overeenkomt. Op basis van deze hoge correlaties kunnen we concluderen dat de WPV en APV equivalent zijn. Deze onderzoeksresultaten ondersteunen de begripsvaliditeit en betrouwbaarheid van de APV.
3. Normgroepen
De normgroepen zijn gebaseerd op data verkregen in echte advies (N=3000)- en selectiesituaties (N=1000), en zijn representatief voor de beroepsbevolking wat betreft geslacht, leeftijd en opleidingsniveau.
4. Handleiding voor testgebruikers
De APV kan toegepast worden bij alle vraagstukken waarbij inzicht in de persoonlijkheid van belang is, zowel in selectie- als adviessituaties. Omdat de afnameduur van deze vragenlijst erg kort is, is de toepassing zeer veelzijdig. U kunt denken aan selectieassessments, coaching en loopbaanadviessituaties.
1. Uitgangspunten bij de testconstructie
2. APV V1: Betrouwbaarheid en validiteit
4. Handleiding voor testgebruikers
Introductie
De Adaptieve Persoonlijkheid Vragenlijst, afgekort APV, is een persoonlijkheidsvragenlijst die voor het werkveld van Human Resource Management (HRM) is ontwikkeld door Ixly B.V. De APV is de adaptieve variant van de Werkgerelateerde Persoonlijkheidsvragenlijst (WPV), die in 2012 overwegend positief beoordeeld is door de Cotan. De APV rapporteert op vijf factoren, die op hun beurt weer in 25 factoren zijn onderverdeeld. De APV kan zowel in advies- als in selectiesituaties ingezet worden.
De APV is een multidimensionale adaptieve persoonlijkheidsvragenlijst. Om de complexe materie begrijpelijk te maken beginnen we met een korte introductie over ééndimensionale itemresponstheorie met twee mogelijke antwoorden (0/1 of “goed”/”fout”). Vervolgens breiden we de discussie uit naar ééndimensionale itemresponstheorie voor Likert-schalen met 5 opties (zoals bij de APV), om vervolgens de overstap te maken naar multidimensionale itemresponstheorie (MIRT) en adaptief testen op basis van MIRT.
1. Uitgangspunten bij de testconstructie
1.1. Voordelen adaptief testen
Adaptief testen heeft een aantal voordelen ten opzichte van klassieke, lineaire tests. De kandidaat krijgt items te zien op basis van eerder gegeven antwoorden. Hiermee vermijden we dat een kandidaat items te zien krijgt die voor hem of haar irrelevant zijn. Door het gebruik van een adaptieve test zijn we dus in staat om in veel kortere tijd een zeer betrouwbare meting van devermogens van de kandidaat te bereiken, omdat er geen ‘nutteloze’ items bevraagd worden (Hambleton, Swaminathan, & Rogers, 1991; Weiss & Kingsbury, 1984). Dit werkt kostenbesparend in het geval de kandidaat de test op locatie maakt. Ook vragen we op deze manier minder tijd van de kandidaat. Bovendien zorgt dit ervoor dat er nauwkeuriger gemeten kan worden (Hambleton et al., 1991; Weiss & Kingsbury, 1984).
Bij cognitieve tests wordt aangenomen dat dit alles leidt tot een verhoogde motivatie bij het maken van de test ten opzichte van klassieke, niet adaptieve tests (Linacre, 2000; Mead & Drasgow, 1993; Sands & Waters, 1997; Weiss & Betz, 1973). Mensen met een lager niveau raken minder gedemotiveerd of afgeschrikt door te moeilijke items, terwijl mensen met een hoger niveau niet verveeld worden of onoplettend door te makkelijke items gaan (Wise, 2014). Echter, andere onderzoeken suggereren dat adaptief testen gepaard kan gaan met demotivatie bij testnemers, bijvoorbeeld omdat ze tussendoor geen makkelijkere items krijgen (om weer even ‘op adem te komen’/bevestigd te worden in hun kunnen) en geen vragen kunnen overslaan (Frey, Hartig, & Moosbrugger, 2009; Hausler & Sommer, 2008; Ortner, Weisskopf, & Koch, 2013; Tonidandel, Quiñones, & Adams, 2002). Het is echter niet aannemelijk dat dit negatieve effect van adaptief testen ook geldt voor persoonlijkheidsvragenlijsten zoals de APV; hier spreken we immers niet van ‘makkelijke’ of ‘moeilijke’ items.
Verder is bekend bij cognitieve tests dat wanneer het adaptieve karakter van de test wordt uitgelegd in de instructies, dit een belangrijke positieve invloed heeft op de motivatie in en prestaties op adaptieve tests (Wise, 2014). Daarom is ervoor gekozen de adaptieve procedure (weliswaar op simpele wijze) uit te leggen in de instructies van de APV.
1.2. Eéndimensionale itemresponstheorie
1.2.1. Het 2PL model
Bij de APV maken we gebruik van itemresponstheorie (IRT, zie bijvoorbeeld Hambleton, Swaminathan, & Rogers, 1991, en Embretson & Reise, 2000). Het doel van IRT is om de latente (dus niet geobserveerde) score, θ of ‘theta’, van iemand op een bepaald construct (bijvoorbeeld intelligentie of een persoonlijkheidstrek) te meten. Het is belangrijk om te noemen dat IRT- modellen draaien om kans. Gegeven bepaalde karakteristieken van items (bijvoorbeeld de moeilijkheidsgraad en de mate van discriminatie van het item), hoe groot is de kans dan dat iemand deze goed of fout beantwoordt? Het grote voordeel van IRT is dat de kenmerken van personen en items op dezelfde schaal kunnen worden weergegeven, waardoor we uitspraken over deze kansen kunnen doen.
Een voorbeeld van een veel gebruikt IRT-model in het cognitieve domein is het Two-Parameter Logistic (2PL) Model. We bespreken dit model hier omdat het model dat we gebruiken bij de APV, het Graded Response Model (Samejima, 1969), de uitbreiding van het 2PL model is voor Likert- schalen. In de discussie hieronder gaan we eerst nog uit van twee mogelijke antwoorden, namelijk goed (1) en fout (0). De kans op een goed antwoord, x = 1, op een bepaald item, gegeven iemands θ komt in het 2PL-model overeen met:
(1.1)
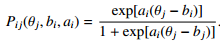
Het subscript j geeft aan dat het om een karakteristiek van een persoon gaat. In de vergelijking is bi de moeilijkheid van een item i, en ai de discriminatie parameter. De specifieke betekenis van ai en bi worden in de volgende secties verder uiteengezet.
Het is belangrijk om hier op te merken dat de waarden van bi en ai in de praktijk altijd bekend zijn: deze itemkenmerken worden geschat (“gekalibreerd” in IRT termen) op basis van onderzoek, wat ook bij de APV gebeurd is (zie sectie 1.4). Dit betekent dat we voor verschillende waarden van θ kunnen bepalen hoe groot de kans is dat een item goed beantwoord wordt. Wanneer we verschillende waarden voor θ invullen kunnen we de itemresponsfunctie plotten (zie Figuur 1.1), waarin de ‘kans op een goed antwoord’ afgezet wordt tegen θ.
Figuur 1.1. Itemresponsfunctie 2PL-mo
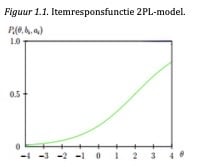
1.2.2. Het schatten van theta
Deze kansen vormen de basis van de berekening van θ. Gegeven dat er in een test k aantal items zijn, is de likelihood functie van een bepaald responspatroon (bijvoorbeeld ‘goed, fout, goed’, of ‘1,0,1’) gelijk aan:
Hierbij is Q de kans op een fout antwoord, oftewel 1 – Q. De likelihood van het responspatroon
‘goed, fout, goed’, of ‘1,0,1’, is dus Pitem1 x Qitem2 x Pitem3.
Op basis van deze likelihood wordt θ geschat: om de waarde van θ te vinden, wordt deze likelihood L gemaximaliseerd (oftewel, gekeken bij welke theta de top van deze functie ligt). Er zijn verschillende manieren om de maximale waarde van de likelihood functie te vinden. In de APV berekenen we θ’s door middel van de maximum a posteriori methode (MAP). Dit is een Bayesiaanse methode, wat betekent dat we ervan uitgaan dat een persoon (dus θ) getrokken is uit een populatie (bij ééndimensionale IRT is dit de populatie met een standaardnormale verdeling met gemiddelde 0 en standaarddeviatie van 1). Deze standaardnormale verdeling wordt de prior genoemd, en hiermee wordt de likelihood functie gewogen. Dit betekent dat L gewogen wordt met de kans dat we de geschatte θ vinden. Het gaat te ver om hier in detail uit te leggen hoe dit werkt, maar uiteindelijk is het maximum van de nieuwe gewogen likelihood functie (de posterior verdeling) de geschatte θ. De standaarddeviatie van deze posterior verdeling geeft de spreiding aan die rondom de geschatte θ verwacht mag worden: hoe kleiner deze spreiding, hoe nauwkeuriger de meting. Deze waarde wordt de standard error of measurement (SEM) of standaardfout genoemd. Deze SEM-waarde is belangrijk bij adaptieve tests en vragenlijsten, omdat deze SEM gebruikt wordt als het stopcriterium van de test (zie sectie 1.4.4). Voor meerinformatie over de schatting van θ verwijzen we de geïnteresseerde lezer door naar De Ayala (2013).
De schatting van θ is gebaseerd op de gegeven antwoorden van een persoon. Bij adaptief testen wordt na ieder gegeven antwoord de θ opnieuw berekend met de tot dan toe gegeven antwoorden. De nauwkeurigheid waarmee θ geschat is, wordt aangegeven door de SEM. Als de θ nauwkeurig genoeg geschat is, met andere woorden als de SEM laag genoeg is, stopt de test (zie sectie 1.4.4).
1.2.3. Het Graded Response Model
In de discussie hiervoor hebben we ons beperkt tot ééndimensionale IRT (dus waar één latente trek θ gemeten wordt) en binaire data (dus goed/fout of 0/1). De APV hanteert een vijf-punts Likert-schaal uiteenlopend van Helemaal oneens tot en met Helemaal eens. Voor data verkregen via Likertschalen zijn er meerdere IRT-modellen ontwikkeld. Eén van de meest gebruikte modellen voor dit type data is het Graded Response Model (GRM; Samejima, 1969), een model dat ontwikkeld is voor geordende responsen, wat antwoorden op Likert-schalen feitelijk zijn.
Het GRM is een uitbreiding van het 2PL model zoals weergegeven in formule 1.1. Bij het GRM heeft elk item één a-parameter (discriminatie), en meerdere locatieparameters (b), waarbij het aantal locatieparameters gelijk staat aan het aantal antwoordcategorieën minus één (dus bij een vijf- punts-schaal zijn er vier locatieparameters). Het GRM is een cumulatief model, dat wil zeggen dat op basis van de itemparameters in eerste instantie de kans geschat wordt dat iemand in een bepaalde categorie of hoger scoort. Dus, de kans op een bepaalde antwoordcategorie of hoger op een bepaald item, gegeven iemands θ, komt in het GRM-model overeen met:
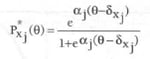
Gezien het feit dat alle kansen logischerwijs op moeten tellen tot 1, kan de kans op een bepaalde gegeven antwoordcategorie als volgt berekend worden.
pk = Pk* - Pk*+1,
De kans op de tweede antwoordcategorie wordt als volgt berekend:
De kansen op de derde en vierde antwoordcategorie worden op een gelijksoortige wijze berekend.
De kans op de laatste antwoordcategorie is simpelweg de laatste cumulatieve kans:
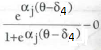
Net als bij het 2PL model is er bij het GRM een itemresponsfunctie, bij het GRM een categorieresponsfunctie genoemd, te plotten voor ieder item. Twee voorbeelden van items van de Competitie-schaal van de WPVN zijn weergegeven in Figuur 1.2.
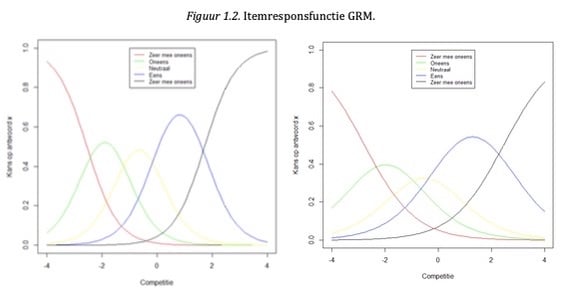
Het schatten van de theta is bij het GRM niet anders dan bij het 2PL model; op basis van de gegeven antwoorden wordt de likelihood bepaald en bijvoorbeeld door middel van de MAP methode naar het maximum van de likelihood functie gekeken om de theta te vinden waarbij het gevonden antwoordpatroon het meest waarschijnlijk is.
1.3. Muldimensionale itemresponstheorie
In het voorgaande hebben we ons beperkt tot ééndimensionale IRT, dus waarbij er steeds slechts één latente trek werd geschat. Bij de APV maken we gebruik van multidimensionele IRT (MIRT), waarbij het doel is om niet één maar meerdere latente trekken tegelijkertijd te schatten.
1.3.1. Between-item versus within-item modellen
Er is een groot scala aan IRT-modellen die geschikt zijn voor multidimensionale adaptieve tests. Een eerste keuze die echter gemaakt dient te worden is of er uitgegaan wordt van between-item multidimensionaliteit of within-item dimensionaliteit (Figuur 1.3.).
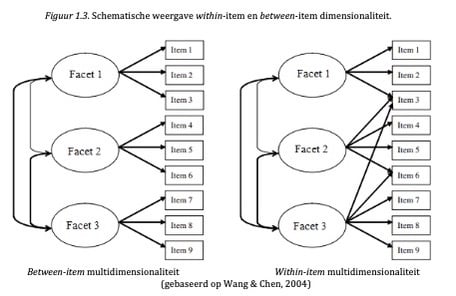
Bij between-item multidimensionale modellen wordt aangenomen dat elk item slechts een indicator is van één latente trek (dus slechts op één trek laadt); multidimensionaliteit wordt gemodelleerd door de correlaties tussen de latente trekken (de dubbelzijdige pijlen aan de linkerkant van het figuur). Belangrijk om hierbij te onthouden is dat bij between-item multidimensionaliteit het antwoord op een vraag slechts afhankelijk is van één latente trek.
Bij within-item multidimensionaliteit kan een item één latente trek of meerdere latente trekken meten: in Figuur 1.3. hierboven zien we bijvoorbeeld dat item 6 een indicator is van Facet 2 en Facet 3. Binnen het domein van intelligentie kan dit bijvoorbeeld een item zijn dat zowel leesvaardigheid als rekenvaardigheid meet. Het ene model is niet per se beter dan het andere; het gaat erom van welk theoretisch model men uitgaat. De keuze tussen beide modellen kennen we overigens uit de (confirmatieve) factoranalyse: between-item multidimensionaliteit reflecteert modellen met een simple structure, terwijl within-item multidimensionale modellen overeenkomen met complexe modellen die kruisladingen toestaan.
In termen van itemresponse theorie betekent between-item dimensionaliteit dat slechts één discriminatieparameter > 0 is, terwijl alle overige discriminatieparameters per definitie 0 zijn (en dus niet geschat worden). Dus, in het linker paneel van bovenstaande figuur heeft Item 1 drie discriminatieparameters, bijvoorbeeld met een waarde 1.5 voor Facet 1, en twee discriminatieparameters voor Facet 2 en Facet 3. Ter illustratie zijn hieronder mogelijke waarden voor discriminatieparameters weergegeven voor een between-item multidimensionaal model.

Voor de APV hebben wij gekozen voor between-item multidimensionaliteit. Voor een deel was dit een pragmatische en praktische keuze: een between-item multidimensionaal model is eenvoudig, intuïtief, en sluit aan bij de traditie van factoranalyse om zoveel mogelijk uit te gaan van simple structures waarbij een item slechts één indicator is van een latente trek. Bovendien is een between- item model consistent met hoe de items ooit ontwikkeld zijn, namelijk om zo goed mogelijk één latente trek te meten. Ook voor de uiteindelijke eindgebruiker is een between-item model eenvoudiger uit te leggen dan een within-item model. Hier komt bij dat gezien het grote aantal items van de originele WPV Normatief (die als itembank dient), er enorm veel mogelijke kruisladingen zijn. Het is niet eenvoudig aan te tonen dat de ene kruislading wel in het model thuishoort, en een ander niet; bovendien loopt men bij kruisladingen het risico dat er gekapitaliseerd wordt op kans, en dat deze niet generaliseren naar verschillende steekproeven (Hopwood & Donnellan, 2010). Het between-item model heeft, omdat elke respons slechts afhankelijk is van één trek, het bijkomend voordeel dat bepaalde analyses (bijv. voor differential item functioning, zie Hoofdstuk 3.3) uitgevoerd kunnen worden – zonder al te veel verlies van statistische power – alsof de data ééndimensionaal is. Dit alles in ogenschouw nemend hebben wij gekozen voor het between-item model.
1.3.2. Het schatten van theta bij multidimensionele IRT
Conceptueel is het schatten op basis van MIRT niet zo heel anders dan bij IRT. Dit is zeker het geval bij between-item modellen, omdat het antwoord op een vraag nog steeds slechts afhangt van één latente trek, net als bij ééndimensionale IRT. Bij ééndimensionale IRT gaven we aan dat bij methoden als MAP ervan uitgegaan wordt dat een persoon (dus θ) getrokken is uit een populatie met een normale verdeling met een gemiddelde van 0 en een standaardafwijking van 1. Bij de MAP methode bij MIRT gaan we ervanuit dat een persoon (in dit geval dus meerdere theta’s tegelijk) getrokken is uit een multivariate normale verdeling met gemiddelden gelijk aan μ, en (co)variantiematrix Φ. In de praktijk wordt deze prior, dus de gemiddelden μ en(co)variantiematrix Φ op basis van een zeer grote steekproef geschat in de kalibratiefase van de testontwikkeling (zie sectie 1.4.1). Een duidelijk verschil tussen het schatten van theta(‘s) bij IRT en MIRT is dus de gehanteerde prior die informatie toevoegt aan de likelihood.
Een ander verschil is dat er bij IRT sprake is van één likelihood functie, bij MIRT zijn er evenveel functies als te schatten theta’s (in het geval van de APV zijn dit er 25). De schatting van de theta’s met behulp van de MAP-methode werkt overigens wel hetzelfde bij MIRT als bij IRT: op basis van een gegeven antwoordpatroon wordt nu gezocht naar theta’s waarbij de verschillende likelihood
functies, gewogen met de prior, allemaal tegelijkertijd maximaal zijn. Bij IRT kan het vinden van het maximum van theta nog numeriek opgelost worden, bij MIRT moet dit echter via een iteratief proces gebeuren; op basis van verschillende iteraties wordt naar de theta’s gezocht waar de verschillende likelihood functies maximaal zijn. Er zijn verschillende algoritmes ontwikkeld om dit soort optimalisatie problemen op te lossen; bij de APV gebruiken we het Broyden–Fletcher– Goldfarb–Shanno (BFGS) algoritme.
Een volledige discussie van MIRT zou hier te veel ruimte kosten, maar de geïnteresseerde lezer verwijzen we door naar Reckase (2009). Belangrijk om hier nog te benoemen is het grote voordeel van MIRT: de relaties tussen latente trekken onderling worden benut om tot een nauwkeurigere schatting van de theta’s te komen (door middel van de prior zoals hiervoor besproken), en bij de itemselectie in de adaptieve test (zie sectie 1.4.3.).
1.4. Ontwikkeling van de APV
Een adaptieve test, zo ook de APV, bestaat uit een aantal vaste onderdelen:
-
Itempool met bekende itemparameters (sectie 1.4.1.)
-
Itemselectie (sectie 1.4.3.)
-
Startregel (het is gebruikelijk om bij adaptieve testen uit te gaan van een gemiddelde
score, dus θ = 0. Deze regel hanteren we ook bij de APV.)
-
Stopregel (sectie 1.4.4.)
De methode van de θ-schatting is feitelijk ook een onderdeel van een adaptieve test, maar deze is in de voorgaande sectie al besproken (de multidimensionale variant van de MAP-methode). In dit hoofdstuk wordt de ontwikkeling van en de gemaakte keuzes voor elk onderdeel van de eerste versie van de APV kort beschreven.
1.4.1. Itempool
1.4.1.1. Eerste kalibratie
Iedere adaptieve test of vragenlijst begint met een itempool, dus een verzameling vragen die getoond kunnen worden aan de kandidaat. Bij de APV vormden de items van de reguliere WPV-N de itempool; hier moesten echter wel nog de itemparameters voor berekend worden. Hiervoor is een kalibratieonderzoek uitgevoerd, wat hieronder besproken wordt. In deze kalibratie werd er tevens onderzoek gedaan naar de juistheid van de gekozen modellen, en naar alternatieve mogelijkheden. De resultaten van deze onderzoeken worden hieronder ook besproken.
De WPV wordt ingezet in zowel advies- als selectiesituaties. Bij de ontwikkeling van de APV was dan ook het doel dat deze bruikbaar zou zijn voor beide testsituaties. In eerste instantie is begonnen met de ontwikkeling van de APV voor adviesdoeleinden, waarna later (zie sectie 3.3) gekeken is of de APV ook inzetbaar zou zijn in selectiesituaties. De onderzoeken tot en met sectie 3.1. zijn dus allen gebaseerd op data verkregen in adviessituaties.
Voor de eerste kalibratie en onderzoeken voor de keuze van het IRT-model zijn de behaalde scores van kandidaten die de WPV Normatief hadden ingevuld, opgehaald uit de Ixly database. Het ging hier om kandidaten die de WPV Normatief daadwerkelijk in adviessituaties hadden ingevuld; de kalibratie en onderzoeken zijn dus gebaseerd op personen die de vragenlijst gemaakt hebben onder dezelfde condities als waar de vragenlijst uiteindelijk voor dient. In totaal hadden we van 9242 personen gegevens over het geslacht, leeftijd en opleidingsniveau tot onze beschikking. Deze informatie is weergegeven in Tabel 1.2.
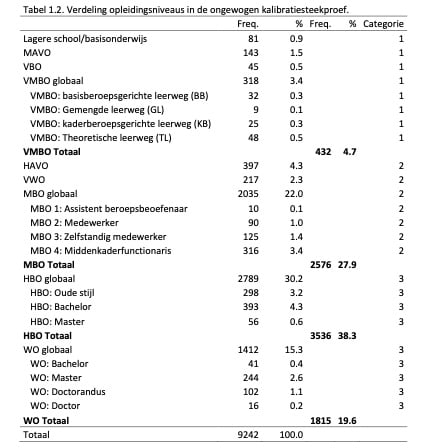
Tijdens de periode van dataverzameling is een aantal keer de achtergrondkenmerken veranderd; zo werd eerst bijvoorbeeld meer algemeen naar de categorieën VMBO, MBO, HBO en WO gevraagd, terwijl dit later fijnmaziger werd bevraagd met specifiekere opleidingsniveaus (bijv. MBO 1). Vandaar dat deze meer algemene groepen (‘globaal’ in Tabel 1.2.) en specifiekere groepen zijn weergegeven in Tabel 1.2.
Uiteindelijk zijn deze groepen gecombineerd in drie categorieën die zo goed mogelijk de categorieën van het CBS weerspiegelen. Deze categorieën zijn weergegeven in de uiterst rechtse kolom. De verdeling wat betreft opleidingsniveaus wat betreft deze drie categorieën is weergegeven in Tabel 1.3.

De verdeling wat betreft geslacht en leeftijd in de ongewogen kalibratiestreekproef is weergegeven in Tabel 1.4.
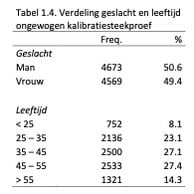
De representativiteit van deze steekproef wat betreft geslacht, leeftijd en opleidingsniveau is vergeleken met de verdeling van deze drie achtergrondkenmerken in de Nederlandse beroepsbevolking in 2017 volgens de gegevens van het CBS. Uit de Chi2-toetsen bleek dat er een klein verschil in verdeling wat betreft geslacht was (χ2(1) = 19.61, p < .001, Cramer’s V = .05), een klein tot gemiddeld verschil wat betreft leeftijd (χ2(4) = 703.25, p < .001, Cramer’s V = .14) en een gemiddeld tot groot verschil wat betreft opleidingsniveau (χ2(2) = 2124.65, p < .001, Cramer’s V = .34). Er bevonden zich in onze steekproef relatief minder jongeren, en meer mensen van middelbare leeftijd (35 – 45 jaar). In onze steekproef bevonden zich relatief veel hoger opgeleiden en minder laag opgeleiden.
1.4.1.2. Gewogen steekproef
Om te corrigeren voor de verschillen tussen onze steekproef en de Nederlandse beroepsbevolking is een wegingsprocedure uitgevoerd. Allereerst zijn er 2 (geslacht) x 5 (leeftijd) x 3 (opleiding) = 30 strata gecreëerd waarna uit deze strata willekeurig een aantal personen werd getrokken met als doel (1) de verdeling wat betreft achtergrondkenmerken van het CBS zoveel mogelijk te benaderen en (2) de uiteindelijke steekproefgrootte op 3000 personen uit te laten komen. Deze grootte hielden we aan omdat we bepaald hadden dat bij een N van 3000 de balans optimaal was tussen een zo groot mogelijke steekproef en een zo klein mogelijke afwijking van de CBS verdelingen wat betreft geslacht, leeftijd en opleiding. Na weging was er geen verschil in verdeling wat betreft geslacht tussen de gewogen steekproef en het CBS (χ2(1) = .01, p = .91). Er waren slechts kleine tot gemiddelde verschillen voor leeftijd (χ2(4) = 41.89, p < .001, Cramer’s V = .06) en opleiding (χ2(2) = 30.82, p < .001, Cramer’s V = .07). De verdeling wat betreft geslacht, leeftijd en opleidingsniveau in de gewogen Adviesnormgroep is weergegeven in Tabel 1.5.
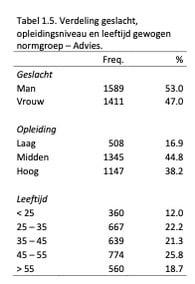
Helaas is er in de itemresponstheorie literatuur – en zeker in de literatuur over multidimensionale IRT – geen eenduidige richtlijn wat betreft de minimale steekproefgrootte voor een accurate schatting van de itemparameters (de kalibratie). Uit recent onderzoek dat specifiek op dit onderwerp focuste, is gebleken dat een steekgroep van N = 1000 een nauwkeurige schatting van itemparameters opleverde, en dat grotere steekproeven niet tot betere schattingen leidden; echter, dit onderzoek ging uit van slechts drie gecorreleerde trekken (Jiang, Wang & Weiss, 2016). In de APV hanteren we maar liefst 25 gecorreleerde schalen; het is dus lastig de resultaten van dit onderzoek naar onze situatie te generaliseren. Door een steekproefgrootte van N = 3000 te hanteren weten we in ieder geval dat we ruim boven de bovengrens van N = 1000 uit dit artikel zitten.
1.4.1.3. Standaardfouten van itemparameters bij verschillende kalibratiesteekproeven
Om de invloed van de grootte van de kalibratiesteekproef te onderzoeken hebben we gekeken naar de grootte van de standaardfouten van de geschatte itemparameters in beide kalibraties; hoe kleiner de standaardfout, hoe nauwkeuriger de schatting van de itemparameter. De gemiddelde itemparameters en standaardfouten zijn weergegeven in Tabel 1.6.
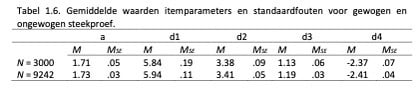
Uit Tabel 1.6. blijkt dat standaardfouten van de parameters een stuk kleiner zijn bij de grote, totale steekproef. In absolute zin is het verschil bij de eerste drempelwaarde (d1) het grootst, maar bij de derde drempelwaarde (d3) zien we dat de standaardfout bij de totale steekproef maar liefst de helft is van die bij de gewogen steekproef. Overigens valt op dat de gemiddelde waarden van de parameters zelf weinig verschillen tussen de steekproeven.
Uit bovenstaande analyse van de gemiddelde standaardfouten blijkt al dat bij de totale steekproef de itemparameters nauwkeuriger geschat worden dan bij de gewogen steekproef. Dit wordt nog duidelijker wanneer we kijken naar de maximale standaardfouten: voor de a-parameter was dit .05 (totaal) vs. .09 (gewogen), voor d1 .34 vs. 1.01, voor d2 .23 vs. .38, voor d3 .10 vs. .16 en voor d4 .10 vs. .17. Met name voor de d1 waarde is het verschil zeer groot; op basis van deze analyses hebben we besloten de eerste kalibratie te doen op de totale steekproef.
De invloed hiervan op de theta-schattingen hebben we bekeken door voor beide kalibraties de geschatte theta’s te vergelijken. In Tabel 1.7. zijn deze gemiddelde verschillen tussen de theta’s op basis van beide kalibraties weergegeven.
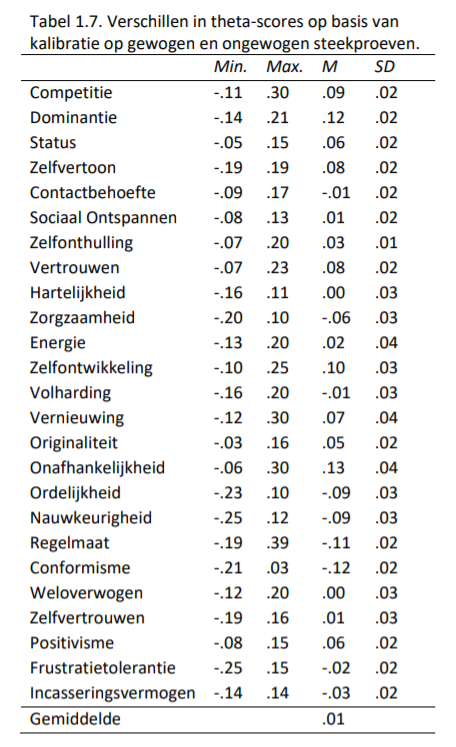
Uit Tabel 1.7. blijkt dat de theta-waarden geschat op basis van de gehele steekproef en de gewogen steekproef nauwelijks van elkaar verschilden. Het gemiddelde verschil was .01, en het maximaal gevonden verschil was .30. Dus, de keuze om de itemparameterschattingen op basis van de ongewogen steekproef te nemen in verband met de grotere nauwkeurigheid (kleinerestandaardfouten), heeft uiteindelijk weinig invloed gehad op de geschatte theta’s.
1.4.2. Keuze van modellen
1.4.2.1. Het itemrespons model: GPCM vs GRM
Er zijn verschillende IRT-modellen ontwikkeld voor Likert-achtige vragenlijsten, waarbij het GRM en het Generalized Partial Credit Model (GPCM; Muraki, 1992) de meest gehanteerde zijn. Het ene model is niet per definitie beter dan het andere, de twee modellen verschillen voornamelijk in de assumpties waar ze op gebaseerd zijn. Om te onderzoeken welk model in ons geval het beste zou zijn, zijn beide modellen toegepast op de WPV-N data, waarna de fit van de modellen en de nauwkeurigheid van de theta-schattingen op basis van beide modellen vergeleken zijn.
In Tabel 1.8. zijn de fitwaarden en betrouwbaarheden (gemiddeld over de 25 schalen) voor de modellen op basis van het GRM en GPCM weergegeven.
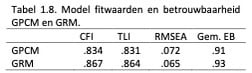
Hoewel de fitwaarden niet heel sterk van elkaar verschilden, zien we dat de waarden voor het GRM net wat beter waren dan voor het GPCM. Bovendien was de empirische betrouwbaarheid bij het GRM ook wat hoger: voor elke schaal gold dat de betrouwbaarheden allemaal .01 tot .03 hoger waren in het GRM. Ook zagen we dat de discriminatieparameters hoger waren in het GRM, wat aanduidt dat het GRM over het algemeen meer informatie levert dan het GPCM, wat de nauwkeurigheid van de metingen ten goede zal komen. Op basis van deze analyses werd duidelijk dat het GRM beter presteerde dan het GPCM; daarom hebben we voor de APV voor het GRM gekozen.
1.4.2.2. Keuze voor het factormodel
Naast de keuze tussen verschillende IRT-modellen, kan er, wanneer er eenmaal voor een variant gekozen is, natuurlijk voor verschillende factormodellen gekozen worden. In ons geval hebben we daarom twee modellen met elkaar vergeleken: een model waarbij de 25 schalen geschat werden samen met de correlaties tussen deze schalen, en een model met een zogenaamde two-tierstructuur (Figuur 1.4.). In dit laatste model worden de 25 schalen geschat, evenals de hogere orde factoren Invloed, Sociabiliteit, Gedrevenheid, Structuur en Stabiliteit, en de correlaties tussen deze vijf factoren. In Tabel 1.9. zijn de fitwaarden van deze modellen weergegeven.
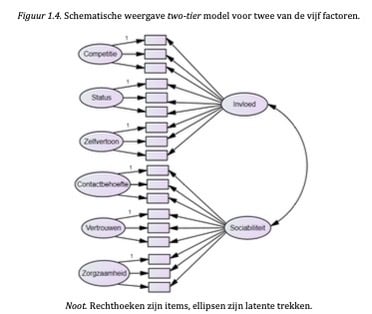
Uit Tabel 1.9. blijkt dat het model met 25 gecorreleerde schalen een betere fit geeft dan het two- tier model: het verschil in χ2 waarden is significant, en de AIC en BIC waarden zijn lager (lagere waarden indiceren een betere fit). Op basis van deze analyses hebben we gekozen voor een model met 25 gecorreleerde schalen.

1.4.2.3. Lokale onafhankelijkheid: analyse van residuen
Eén van de assumpties van IRT is lokale onafhankelijkheid; dit houdt in dat iedere samenhang tussen twee items volledig verklaard moet kunnen worden door de latente trek(ken) die deze items meten. Dus, de kans op een respons op een item (wat construct X meet) zou niet gerelateerd moeten zijn aan de kans op een respons op een ander item (van construct X) voor respondenten met dezelfde theta. In statistische termen betekent dit dat de itemresiduen ongecorreleerd zouden moeten zijn. Of dit het geval is hebben wij onderzocht bij de APV door voor elke itemcombinatie (in totaal 300) de residuen te berekenen (met behulp van de residuals functie in het mirt pakket (Chalmers, 2012) voor R; R Core Team, 2017). Deze residuen zijngestandaardiseerd, en vervolgens te interpreteren als Cramer’s V-waarden met 4 vrijheidsgraden (het aantal antwoordcategorieën – 1). Deze waarden zijn vervolgens te kwalificeren als klein, gemiddeld en groot aan de hand van richtlijnen van Cohen (1988). In Tabel 1.10. is de indeling van de residuen in deze categorieën weergegeven.

De residuen zijn over het algemeen voldoende; de meeste bevinden zich in de categorie klein – gemiddeld. Analyses van de itemparen die hoge waarden lieten zien, toonden aan dat deze hoge waarden te verwachten waren. Zo werd de maximale waarde (.35) gevonden voor een item van Positivisme (“Voelt zich vaak moedeloos”) en Energie (“Heeft weinig energie”). Moedeloosheid en het hebben van weinig energie zullen vaak synoniem zijn, en zullen dus een hoge mate van overlap laten zien, wat niet helemaal ‘weg verklaard’ kan worden door de schalen Energie en Positivisme en hun correlatie.
Een ander voorbeeld is “Neemt in een groep beslissingen” (Dominantie) en “Stelt zich in gezelschap afwachtend op” (Sociaal ontspannen), met een residu van .26. In dit laatste voorbeeld zorgen de woorden ‘groep’ en ‘gezelschap’ waarschijnlijk voor de residuele correlatie tussen de items; de overeenkomst tussen deze woorden zal ervoor zorgen dat de items meer samenhangen dan verwacht. Het is algemeen bekend dat de bewoordingen in persoonlijkheidsvragenlijsten vaak voor residuele correlaties kunnen zorgen (Hopwood & Donnellan, 2010). Voor een deel is dit dus inherent aan de manier waarop persoonlijkheid via zelfrapportage vragenlijsten gemeten wordt.
Gebaseerd op onze analyses van de residuen en bovenstaande beschreven bevindingen, is geconcludeerd dat de items voldoende mate van lokale onafhankelijkheid laten zien. Alle items zijn daarom in de itempool behouden voor de eerste versie van de APV.
1.4.3. Itemselectie
Na elk gegeven antwoord moet het beste nieuwe item gezocht worden. Het beste item is bij ééndimensionale adaptief tests meestal het item dat de meeste informatie geeft op het interim theta-niveau. De discriminatie-parameter, a, van een item bepaalt hierbij hoe discriminerend, dus hoe informatief een item, is: hoe hoger de discriminatie-waarde, hoe meer informatie een item in principe levert. Echter, de hoeveelheid informatie die een item levert, is afhankelijk van de positie op de theta-schaal (dus hoog iemand scoort op een bepaalde trek). Dit komt naar voren in onderstaande Figuur 1.5., waar de iteminformatiefuncties zijn weergegeven van dezelfde twee items als in Figuur 1.2.:
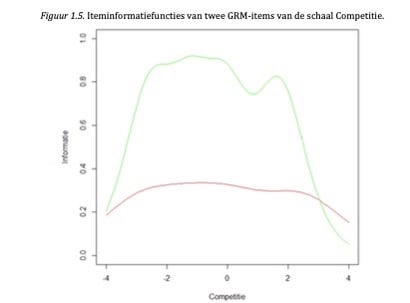
Duidelijk is dat het ene item (de groene lijn) over de gehele linie genomen meer informatie levert dan het andere (de rode lijn); de a-parameter van het rode item is dus hoger dan die van het groene item. Bij de meeste waarden op Competitie zou het groene item dus het beste item zijn om te selecteren in de adaptieve test. Echter, we zien dat bij een zeer hoge mate van Competitie (bijvoorbeeld bij een score van 4) het rode item meer informatie levert dan het rode, en dus voor personen met die score juist het beste item zou zijn. Dit basisprincipe, het tonen van het item dat voor de gegeven theta de meeste informatie oplevert, vormt de basis van de itemselectie bij de APV.
Het bovenstaande is echter van toepassing bij ééndimensionale tests. Bij multidimensionale tests is de uitkomst van de iteminformatiefunctie niet één waarde, maar een matrix (in ons geval een 25x25 matrix), en afhankelijk van alle 25 theta’s tegelijk. Bovendien wordt in het Bayesiaanse multidimensionale model dat wij hanteren (Segall, 1996) aan de informatiematrix ook nog de prior informatie toegevoegd, door deze prior bij de informatiematrix op te tellen. Deze prior is de inverse van de correlatiematrix tussen de schalen van de test of vragenlijst. De informatiewaarde van een item wordt vervolgens bepaald door de determinant (vandaar de naam D-optimaliteit van deze methode) van de uiteindelijke opgetelde matrix te nemen. Dit levert voor ieder item één getal op, waarbij een hogere waarde meer informatie betekent; in de APV wordt het item met de hoogste waarde getoond.
Net als bij ééndimensionale adaptieve tests zijn er verschillende itemselectie methoden te onderscheiden bij multidimensionale adaptieve tests. Bij de APV hebben we zoals gezegd gekozen voor de D-optimaliteit methode. Deze keuze is deels gebaseerd op eerdere bevindingen bij andere multidimensionale tests uit de literatuur; de D-optimaliteit methode levert een nauwkeurigeschatting van de theta’s op met relatief weinig items (Mulder & Van der Linden, 2009; Yao, 2012). Daarbij bleek uit eerste simulaties dat deze methode ook bij de APV nauwkeurige schattingen opleverde.
Aangezien de APV in totaal 25 schalen meet, moet er in het itemselectie-algoritme voor gezorgd worden dat alle schalen aan bod komen. Gebaseerd op de literatuur (Yao, 2012) is er daarom een weging in het algoritme opgenomen, waarbij items van schalen waar nog weinig informatie over is (dus die nog een hoge SEM hebben) een grotere weging krijgen en dus een grotere kans hebben om getoond te worden.
1.4.4. Stopcriterium
De meest gebruikte stopregel in adaptieve tests is stoppen wanneer de mate van precisie (uitgedrukt in de SEM-waarde van de geschatte latente trek) een bepaalde drempelwaarde bereikt heeft. De test stopt dan wanneer SEM < x is, waarbij x een van te voren bepaald criterium, dus mate van precisie, is. We hebben bij de APV in eerste instantie gekozen voor een waarde van 0.44, wat theoretisch overeenkomt met een betrouwbaarheid van ongeveer .80 (1-0.194 = 0.80; Thissen, 2000). Voor tests die gebruikt worden bij belangrijke beslissingen – zoals personeelsselectie waar de APV mede voor ontwikkeld is – is dit voldoende op schaalniveau (> .80; Cotan, 2009). Een lagere SEM (dus hogere mate van betrouwbaarheid) is ook overwogen, echter, we zagen in simulatiestudies dat met een stopcriterium van .44 de betrouwbaarheden van de schalen hoger (dus de SEM’s lager) uitvielen dan gedacht (zie sectie 2.2). Dit komt door het multidimensionale karakter van de vragenlijst: door middel van onderlinge correlaties geeft een item van de schaal Contactbehoefte bijvoorbeeld ook informatie over de schaal Zelfonthulling. Hierdoor zal wanneer een item van Contactbehoefte getoond wordt ook de SEM van Zelfonthulling naar beneden gaan.
In eerste simulaties viel op dat sommige personen erg veel items nodig hadden, terwijl hun metingen in absolute zin niet nauwkeuriger werden door de extra aangeboden items. Bij de APV streven we naar een zo nauwkeurig mogelijke vragenlijst, maar ook naar een zo kort mogelijke afnametijd om de beleving van de kandidaat te optimaliseren. In de literatuur zijn verschillende oplossingen voorgedragen voor dit probleem; een simpele methode is bijvoorbeeld de adaptieve test te stoppen na een vast aantal items. Een andere, meer complexe methode, is te kijken naar de reductie in SEM, en te stoppen met het aanbieden van items van een bepaalde trek wanneer de reductie in SEM te klein is (Yao, 2013). In simulatiestudies zijn verschillende oplossingen voor dit probleem onderzocht bij de APV. Uiteindelijk bleken bovenstaande twee oplossingen niet gewenst, omdat er of teveel aan nauwkeurigheid ingeboet werd, of omdat het algoritme te complex werd voor afname in de praktijk. Uit de studies bleek dat een maximum van 6 items per latente trek de optimale balans van nauwkeurigheid en afnametijd gaf. Uiteindelijk is er dus voor gekozen om de adaptieve test te stoppen wanneer de SEM < 0.44 is voor alle schalen, of te stoppen wanneer voor iedere schaal al 6 items aangeboden zijn. Gezien de APV 25 schalen meet betekent dit in de praktijk dat het maximale aantal items (25 x 6 =) 150 is.
2. APV V1: Betrouwbaarheid en validiteit
Bij de ongewogen kalibratiesteekproef (N = 9242; zie pagina 12) is de eerste versie van de APV gesimuleerd, waarbij de adaptieve test ingericht werd met de specificaties zoals hiervoor beschreven: de startwaarden van de theta’s werden op 0 gezet, itemselectie op basis van D- optimaliteit, een stopcriterium van SEM < .44, gecombineerd met een limiet van maximaal 6 items per schaal. Op basis van deze simulatie kan de nauwkeurigheid en de validiteit van de adaptief afgenomen vragenlijst vergeleken worden met de volledige, lineaire vragenlijst.
2.1. Validiteit
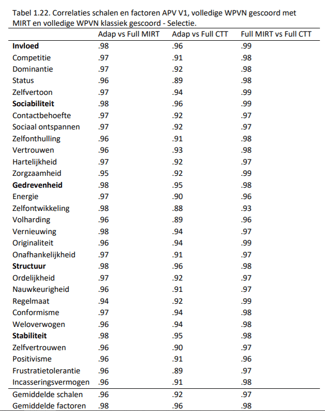
In Tabel 1.11 zijn de correlaties weergegeven van de theta’s uit de adaptieve test en die van de volledige versie van de test, gescoord met MIRT (kolom 2). Ook zijn de correlaties tussen de adaptief verkregen theta’s en de schaalscores (dus berekend volgens klassieke testtheorie) van de volledig afgenomen WPV-N weergegeven (kolom 3). Ter vergelijking zijn in de laatste kolom de correlaties weergegeven tussen de klassiek gescoorde volledige WPV-N en de volledige WPV- N gescoord door middel van MIRT.
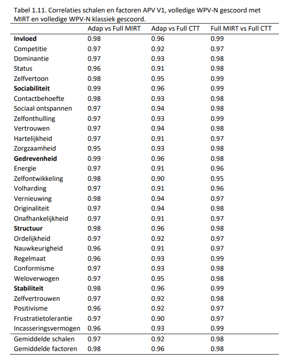
Opvallend in Tabel 1.11. is dat alle correlaties zeer hoog zijn (> .90). De theta-scores op basis van de adaptieve test zijn vrijwel hetzelfde als de theta-scores verkregen op basis van de volledige test (gemiddelde correlatie van .97 voor de schalen en .98 voor de factoren). De rangordering van personen is nagenoeg hetzelfde, zelfs in vergelijking met de volledige WPVN, maar dan klassiek gescoord door middel van somscores van de schalen (gemiddelde correlatie van .92 voor de schalen en .96 voor de factoren). Dit is opvallend, omdat er in de adaptieve test gemiddeld slechts 92 items nodig waren om de theta’s te berekenen, vergeleken met 276 items van de volledige WPV-N (zie sectie 2.3). Dit is een reductie van testtijd van maar liefst twee derde, terwijl dit dus op de meting van de theta’s weinig invloed heeft gehad. Interessant is om tot slot op te merken dat de twee scoremethoden (klassieke testtheorie vs. MIRT) bij de volledige WPV-N nagenoeg dezelfde theta’s opleveren (laatste kolom).
Correlaties zeggen iets over de relatieve verhoudingen tussen variabelen, maar niet over absolute verschillen tussen de scores. Daarom hebben we in Tabel 1.12 de gemiddelde verschillen en de root mean square error (RMSE) weergegeven.
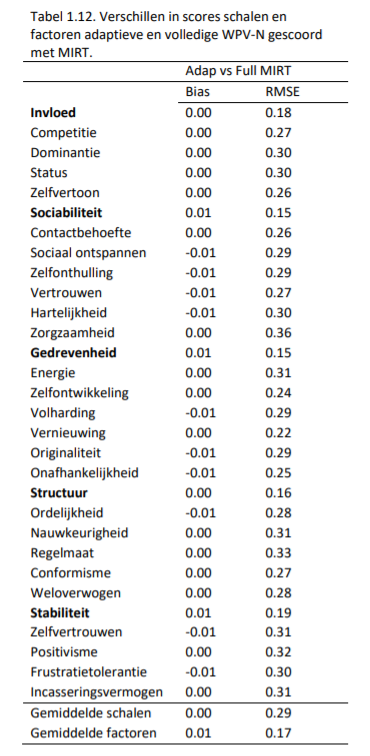
Uit zowel de gemiddelde verschillen als de RMSE-waarden blijkt dat de verschillen tussen de volledige WPV-N en de adaptieve versie te verwaarlozen zijn. Dit betekent dat een persoon ongeveer dezelfde score zal behalen, ongeacht welke versie van de test ingevuld is.
2.2. Betrouwbaarheid
De resultaten zoals weergegeven in Tabel 1.11. en 1.12. geven al een indicatie dat met de adaptieve test de scores van de volledige lineaire test goed benaderd kunnen worden. Dit zegt iets over de validiteit van de metingen, maar nog niet direct iets over de betrouwbaarheid: dus hoe nauwkeurig de metingen precies gedaan worden met de adaptieve vragenlijst. Om hier uitspraken over te doen zijn de betrouwbaarheden van de adaptieve en volledige vragenlijst weergegeven: bij de adaptieve test en de volledige vragenlijst gescoord met MIRT zijn dit de empirische betrouwbaarheden (Du Toit, 2003) en bij de klassiek gescoorde vragenlijst zijn dit Cronbach’s alfa waarden voor de schalen, en Cronbach’s alfa (op basis van de schalen) en generaliseerbaarheden voor de factoren.
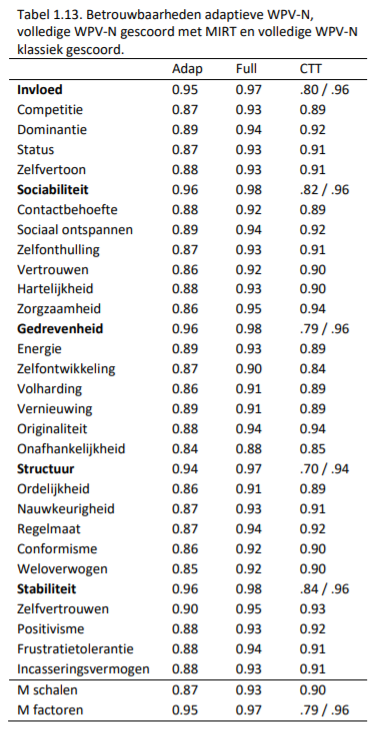
De conclusies op basis van Tabel 1.11. gelden ook voor Tabel 1.13.: hoewel de adaptieve vragenlijst iets aan betrouwbaarheid inlevert, is dit in vergelijking met de volledige versies bijna te verwaarlozen. Zeker als er rekening wordt gehouden met de zeer korte afnametijd, in vergelijking met de volledige test. Dit betekent dat met de adaptieve versie net zo nauwkeurig gemeten kan worden als met de volledige versie van de WPV-N.
2.3. Kenmerken APV V1
Na de simulatie zijn ook een aantal kenmerken van de APV onderzocht. Deze worden hieronder besproken.
2.3.1. Hoeveelheid items en afnametijd
Bij de simulatie waren er gemiddeld 92 items (SD = 11.0) nodig om tot een nauwkeurige schatting van de 25 schalen te komen, met een minimum van 64 en een maximum van 147. Vergeleken met de WPV-N is dit een reductie van 47% tot 77%, met een gemiddelde reductie van 67%. Qua afnametijd betekent dit dat de APV ongeveer 10 tot 25 minuten zal duren, vergeleken met 30 tot 40 minuten bij de WPV-N.
Ook bleek dat bij iedere persoon elke schaal minimaal met twee items bevraagd werd. Over alle gesimuleerde personen heen bleek dat er voor de schaal Competitie gemiddeld slechts 2 items per afname nodig waren, terwijl voor Onafhankelijkheid, Conformisme, Weloverwogen, en Positivisme er gemiddeld 5 items bevraagd werden.
2.3.2. Itemgebruik
Hoewel itembekendheid bij persoonlijkheidsvragenlijsten minder problematisch is dan bij intelligentietests, is het wel informatief om te kijken naar het gebruik van de items uit de itembank. Als er slechts een klein deel van de items gebruikt zou worden, dan zou dit kunnen betekenen dat er te weinig informatieve items in de itembank staan.
Uit analyses bleek dat er een goede spreiding is qua items die getoond worden in de APV. In de simulatie waren er 12 items (4% van de itembank) die niet gebruikt werden, en 6 items (2%) die aan iedere kandidaat getoond werden. Deze verdeling wat betreft gebruik van de itembank is weergegeven in Figuur 1.6.
3. Normen
3.1. Eerste Adviesnormgroep
Bij de gewogen steekproef (zie pagina 13) is de eerste versie van de APV gesimuleerd, waarbij de adaptieve test ingericht werd met de specificaties zoals hiervoor beschreven: de startwaarden van de theta’s werden op 0 gezet, itemselectie op basis van D-optimaliteit, een stopcriterium van SEM < .44, gecombineerd met een limiet van maximaal 6 items per schaal.
Nadat iedere persoon in de gewogen steekproef de APV had doorlopen, zijn de theta-scores genormeerd met de continue fit-methode (zie Van der Woud, 2008). Voor een uitgebreide uitleg over hoe van ruwe scores gekomen wordt tot stenscores verwijzen we naar de handleiding van de WPV Compact (Ixly, 2012, p. 50-55). De kenmerken van de ruwe scores en de stenscores (weergegeven in de rapportage van de APV) zijn beschreven in Tabel 1.14.
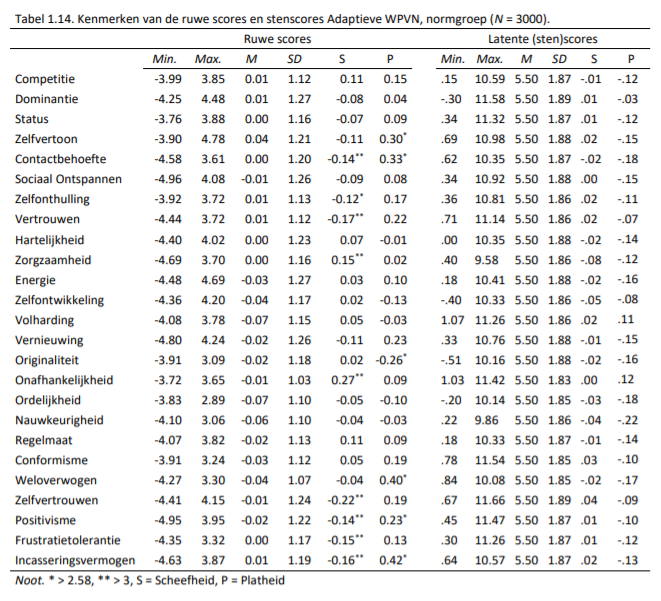
Met een asterisk (*) is aangegeven wanneer de Z-score (verkregen door de waardes door hun standaardfout te delen) van de scheefheid en kurtosis (platheid) de grens ± 2.58 overstijgt. Deze drempelwaarde wordt vaak gehanteerd als indicatie dat een verdeling van de theoretische normale verdeling afwijkt. Er zijn 9 schalen waarbij de ruwe scores een wat schevere verdeling dan verwacht laten zien, en 6 schalen waar de verdelingen een wat hogere piek laten zien dan verwacht. Echter, de vuistregel van ||Z||>2.58 wordt door sommigen als erg streng gekwalificeerd, en zij hanteren daarom liberalere regels waarbij absolute waarden van scheefheid > 3 en kurtosis > 8 (of zelf >10) gelden als een indicatie voor een afwijking van de normale verdeling (Kline, 2005). Gebaseerd op deze regels (zie Tabel 1.14.) kunnen we over het algemeen concluderen dat de ruwe scores van APV redelijk normaal verdeeld zijn in de normgroep.
3.2. Onderzoek naar differential item functioning (DIF) tussen Advies- en Selectiegroep
De WPV wordt ingezet in zowel advies- als selectiesituaties. Bij de ontwikkeling van de APV was dan ook het doel dat deze bruikbaar zou zijn voor beide testsituaties. Ten behoeve hiervan zijn twee belangrijke stappen ondernomen: eerst is onderzocht of de items hetzelfde functioneren wanneer kandidaten de vragenlijst in advies- of in selectiesituaties maken, om vervolgens een representatieve selectienormgroep te creëren. De onderzoeken die hiervoor gedaan zijn worden hieronder besproken.
Allereerst zijn de gegevens en scores opgehaald van kandidaten die de WPV-N daadwerkelijk in selectiesituaties hadden ingevuld. In totaal hadden we van 9110 personen gegevens over het geslacht, leeftijd en opleidingsniveau. De informatie wat betreft opleidingsniveau is weergegeven in Tabel 1.15.
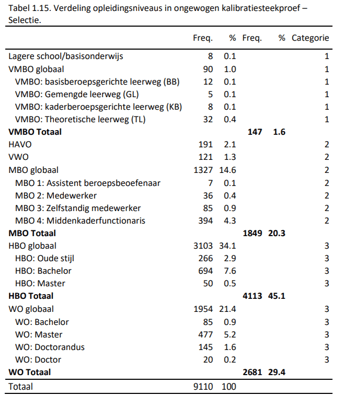
Uiteindelijk zijn deze groepen net als bij de Adviesgroep gecombineerd in drie categorieën die zo goed mogelijk de categorieën van het CBS weerspiegelen. Deze categorieën zijn weergegeven in de uiterst rechtse kolom. De verdeling wat betreft opleidingsniveaus wat betreft deze drie categorieën is weergegeven in Tabel 1.16.
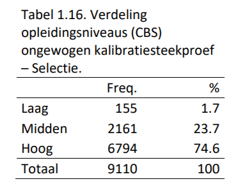
De verdeling wat betreft geslacht en leeftijd in de ongewogen Selectiesteekproef is weergegeven in Tabel 1.17.
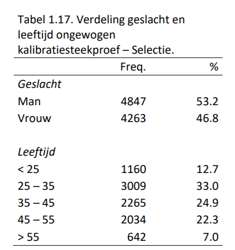
De representativiteit van deze steekproef wat betreft geslacht, leeftijd en opleidingsniveau is vergeleken met de verdeling van deze drie achtergrondkenmerken in de Nederlandse beroepsbevolking in 2017 volgens de gegevens van het CBS. Uit de Chi2-toetsen bleek dat er geen verschil in verdeling wat betreft geslacht was (χ2(1) = 0.43, p = .51), een gemiddeld tot groot verschil wat betreft leeftijd (χ2(4) = 1385.92, p < .001, Cramer’s V = .20) en een groot verschil wat betreft opleidingsniveau (χ2(2) = 6056.91, p < .001, Cramer’s V = .58). Er bevonden zich in onze steekproef relatief meer jongere mensen (25 – 35 jaar), en minder mensen met een hogere leeftijd (35 – 45 jaar). In onze steekproef bevonden zich relatief veel hoger opgeleiden en minder middelbaar en lager opgeleiden.
Wanneer scores van kandidaten verkregen worden via vragenlijsten is het belangrijk dat de vragenlijsten rechtvaardig (fair) zijn: rechtvaardig betekent dat geen onterechte vertekening (bias) ontstaat bij individuele uitkomsten en dat alleen reële verschillen tussen individuen zichtbaar worden in relatie tot de beroepspopulatie. Eén mogelijke veroorzaker van bias is de testsituatie waarin de kandidaat de vragenlijst maakt; het is bekend dat sollicitanten vaak wat sociaal wenselijker antwoorden om zo hun kans op de baan te vergroten. Hoewel we weten dat dit leidt tot (gemiddelde) verschillen tussen scores verkregen in selectiesituaties en andere situaties (bijv. onderzoek of adviessituaties; zie Birkeland, Manson, Kisamore, Brannick, & Smith, 2006), is niet geheel duidelijk in de literatuur wat het effect van de testsituatie op itembias is (zie bijv. O’Brien & LaHuis, 2011; Robie, Zickar, & Schmit, 2001; Stark, Chernyshenko, Chan, Lee, & Drasgow, 2001; Stark, Chernyshenko, & Drasgow, 2004).
Itembias houdt in dat personen uit de ene groep (bijvoorbeeld sollicitanten) op een andere manier reageren op een item of een item anders interpreteren dan een andere groep (bijvoorbeeld personen die een vragenlijst maken voor loopbaanontwikkeling). Om dit te onderzoeken hebben we een aantal DIF (differential item functioning, zie bijvoorbeeld Zumbo, 1999) analyses uitgevoerd: deze analyses toetsen de hypothese dat de scores op items tussen twee personen uit verschillende groepen niet significant van elkaar verschillen, wanneer de (latente) score op het construct dat dit item meet constant gehouden wordt. Met andere woorden, twee personen uit verschillende groepen (bijvoorbeeld een sollicitant en een loopbaan kandidaat) met dezelfde‘ware’ mate van Contactbehoefte moeten dezelfde kans hebben op een bepaald gegeven antwoord (bijvoorbeeld ‘helemaal eens’).
3.2.1. DIF op basis van DFIT
De eerste methode die we gehanteerd hebben is de DFIT-methode (Raju, van der Linden, & Fleer, 1995). In deze methode worden de ‘ware’ scores op basis van itemparameters gekalibreerd op de referentiegroep (Advies) vergeleken met geschatte scores op basis van itemparameters gekalibreerd op de focale groep (Selectie). Hiervoor worden per item de volgende stappen ondernomen:
-
Voor de focale groep worden de itemparameters geschat en vervolgens de theta-scores berekend
-
Voor de referentiegroep worden de itemparameters geschat
-
Vervolgens worden voor de theta’s verkregen bij (1) de voorspelde waarde op een item
berekend op basis van de itemparameters verkregen bij (1) en voor de itemparameters
verkregen bij (2)
-
Vervolgens wordt het gemiddelde genomen van het gekwadrateerde verschil tussen de
voorspelde waarden verkregen onder (3). Dit is de NCDIF-statistiek (Raju et al., 1995).
Wanneer itemkalibraties op twee verschillende steekproeven zijn gebaseerd, dan dienen de itemparameters op dezelfde schaal gezet te worden door middel van linking. In lijn met eerdere onderzoeken (O’Brien & LaHuis, 2011; Raju et al., 1995; Robie et al., 2001) hebben we de adviesparameters gelinkt aan de parameters gekalibreerd op basis van de Selectiegroep. Dit is gedaan volgens de multidimensionale uitbreiding van de methode van Haebara (1980), met behulp van het plink pakket (Weeks, 2010) in R (R Core Team, 2017).
3.2.1.1. Resultaten DIF op basis van DFIT
Gezien de grootte van onze steekproeven hebben we niet gekeken naar de significantieniveaus1 van de NCDIF-waarden maar naar de effectgrootten (ESSD; zie Meade, 2010); deze ESSD-waarden kunnen geïnterpreteerd worden als Cohen’s d-waarden. De gevonden effectgrootten en de interpretatie hierbij is weergegeven in Tabel 1.18.

Uit de analyses bleek dat de meerderheid van de items een geringe mate van DIF vertoonden. Het feit dat de meeste waarden positief zijn, komt overeen met de verwachting dat bij een gelijke ‘ware’ score op een bepaalde trek, personen in een selectiesituatie een hogere kans hebben het eens te zijn met een antwoord omdat ze overal ‘een schepje bovenop doen’. Opvallend was echter wel dat bij iedere schaal er zowel positieve als negatieve DIF plaatsvond, dit betekent dat het niet altijd het geval was dat bij een gelijke score op een bepaalde trek de kans op een positief antwoord altijd hoger was bij de Selectiegroep. Sollicitanten lijken dus niet ongeacht het item een hogere kans op een positief antwoord te hebben.
Slechts 2.2% van de items vertoonden een gemiddeld tot grote mate van DIF. Om te onderzoeken in hoeverre de items die de meeste DIF lieten zien getoond werden in de APV, is gekeken naar de 20 items met de hoogste absolute ESSD-waarden. Hieruit bleek dat deze items gemiddeld in slechts 1.6% van de gevallen aan een kandidaat getoond werden (SD = 2.2, Min. = .01, Max. = 8.3). Hieruit blijkt dat het effect van DIF in de praktijk bij de APV waarschijnlijk weinig invloed op de scores zal hebben.
3.2.1.2. Resultaten DTF op basis van DFIT
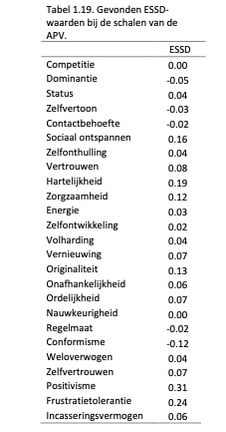
Ook op schaalniveau zijn de ESSD-waarden berekend (zie Tabel 1.19.). Afgaande op de richtlijnen van Cohen (1988) zien we dat de meeste schalen een geringe mate van DTF vertonen, met iets grotere effecten voor Positivisme en Frustratietolerantie (hoewel deze nog steeds als relatief klein beschouwd kunnen worden). De schalen van de APV lijken zich dus niet anders te gedragen in selectiesituaties in vergelijking met adviessituaties.
3.2.2. Ordinale logistische regressie (OLR)
Omdat de statistische power van de verschillende methoden om DIF te detecteren verschilt, wordt aangeraden om meerdere methoden van onderzoek te gebruiken (Wood, 2011). We hebben daarom ook DIF en DTF onderzocht door middel van ordinale logistische regressie (OLR).
Hiervoor hebben we het hiërarchische model van Zumbo (1999) gebruikt:
Model 1: Eerst wordt een ordinale logistische regressie uitgevoerd met het item als de afhankelijke variabele en de totaalscore (theta) op het construct dat door dit item gemeten wordt als onafhankelijke variabele.
Model 2: Vervolgens wordt de groepsvariabele als onafhankelijke variabele ingevoerd (in ons geval Advies/Selectie).
Model 3: Vervolgens wordt de interactie tussen de totaalscore en de groepsvariabele als onafhankelijke variabele ingevoerd.
Er zijn twee voorwaarden die bepalen wanneer we kunnen spreken van substantiële DIF. Allereerst kan de fit van deze modellen aan de hand van hun χ2 waarden vergeleken worden. Als de p-waarde van het verschil in χ2 waarden van Model 3 en Model 1 (met 2 vrijheidsgraden) kleiner is dan 0.01 (een α van 1% is hier nodig, omdat meerdere hypotheses getoetst worden; Zumbo, 1999), dan is Model 3 dus significant beter dan Model 1 en kan er sprake zijn van DIF.
In het voorgaande wordt aangegeven dat er ‘sprake kan zijn van DIF’: onder invloed van bijvoorbeeld de steekproefgrootte, relatieve grootte van de focale- en referentiegroep en de kenmerken van de items kan de χ2-waarde significant worden (Lei et al., 2006; Swaminathan & Rogers, 1990; Zumbo, 1999). De tweede voorwaarde is daarom dat er aanzienlijke effectgrootten moeten zijn voordat er sprake kan zijn van substantiële DIF (Kirk, 1996; Zumbo, 1999; Zumbo & Hubley, 1998). Hiervoor wordt het verschil in verklaarde variantie, ΔR2, tussen de verschillende modellen gebruikt. Jodoin en Gierl (2001) hanteren de categorieën: 0 – .035 als verwaarloosbaar, .035 – .07 als matig en >.07 als sterk. In het huidige onderzoek hanteren we deze vuistregel. Alleen wanneer aan de beide voorwaarden (significantie en een substantiële effectgrootte) voldaan wordt dan kunnen we spreken van substantiële DIF.
Bovenstaande test met 2 vrijheidsgraden kan gezien worden als een omnibus test voor zowel uniforme als non-uniforme DIF. Een manier om vervolgens inzicht te krijgen in de mate van uniforme- en non-uniforme DIF is door de R2-waarden van Model 2 en Model 3 te vergelijken. Het verschil in R2-waarden tussen Model 1 en Model 3 is namelijk additief (bijvoorbeeld ΔR2M3-M1 = .10): de ΔR2 tussen Model 1 en Model 2 is representatief voor uniforme DIF (bijvoorbeeld ΔR2M2- M1 = .08), de ΔR2 tussen Model 3 en Model 2 is representatief voor non-uniforme DIF (bijvoorbeeld ΔR2M3-M2 = .02).
Het effect van DIF op schaalniveau (DTF) kan ook onderzocht worden door:
-
voor ieder item de voorspelde score te berekenen op basis van het geschatte logistische
model
-
voor iedere schaal de voorspelde schaalscore te berekenen door de scores verkregen
onder (1) per schaal te sommeren en
-
deze voorspelde schaalscores in een grafiek af te zetten tegen de theta-scores, met aparte
lijnen voor de Advies- en Selectiegroep.
Voordat we over konden gaan op onze analyses is eerst een gezamenlijke kalibratie uitgevoerd van de Advies- en Selectiegroep. Hiervoor werden deze twee groepen samengevoegd tot één steekproef (N = 18352), waarna eerst de itemparameters voor deze gecombineerde groep werden berekend en vervolgens de theta’s.
3.2.2.1. Resultaten DIF op basis van OLR
Uit de analyses bleek dat 211 van de 276 items (76%) potentiële DIF vertoonden op basis van het significantieniveau (M3 – M1). Echter, zoals vermeld dient ook gekeken te worden naar de effectgrootte. Hieruit bleek dat de maximaal gevonden effectgrootte slechts 0.016 was: dit ligt in de categorie tussen de 0 en 0.035 wat als ‘verwaarloosbaar’ gekenmerkt kan worden. Dit houdt in dat er op basis van deze analyses nauwelijks sprake van DIF op basis van testsituatie blijkt te zijn bij de items van de APV.
3.2.2.2. Resultaten DTF op basis van OLR
Voordat we de resultaten van de DTF analyses toelichten is het interessant om te vermelden dat er, zoals verwacht op basis van de literatuur, verschillen in gemiddelde theta’s waren tussen Advies en Selectie. De gemiddelde Cohen’s d waarde over de 25 schalen was 0.34 (SD = 0.21, Min. = -0.31, Max. = 0.59). Het feit dat deze gemiddelde waarde positief is, duidt erop dat de scores voor de Selectiegroep, zoals verwacht, over het algemeen hoger waren dan voor de Adviesgroep. Ook waren er verschillen in gemiddelde voorspelde schaalscores (gemiddelde Cohen’s d van 0.34). Echter, er bleken weinig verschillen wanneer de behaalde theta-score constant gehouden werd tussen de groepen; de geringe DIF effecten op itemniveau vertaalden zich dus door naar geringe effecten op schaalniveau.
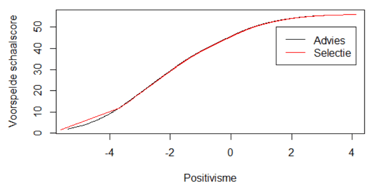
Een voorbeeld hiervan is te zien in Figuur 1.7., voor de schaal Positivisme, waarvoor het verschil in gemiddelde (voorspelde) scores het grootst was (d = 0.60). Uit het figuur is af te lezen dat bij een gelijke score op Positivisme (theta), de voorspelde score op basis van het logistische model nagenoeg hetzelfde is voor Advies en Selectie. Dus, hoewel er verschillen in gemiddelde scores zijn, lijken de schalen van de APV zich niet anders te gedragen in advies- en selectiesituaties.
3.2.3. Conclusie onderzoek DIF en DTF tussen Advies- en Selectiegroep
Op basis van twee verschillende methoden is onderzocht of de items van de APV anders functioneren wanneer deze onder adviessituaties ingevuld worden of onder selectiesituaties. Op basis van de methode van DFIT kwamen er enkele verschillen naar voren, hoewel deze (1) niet erg groot waren en (2) bij items voorkwamen die relatief weinig getoond worden in de APV. Op schaalniveau werden ook verschillen gevonden, maar ook deze waren van geringe grootte. De grootste effecten werden gevonden voor Positivisme en Frustratietolerantie. Hierbij dient ook opgemerkt te worden dat de analyses gebaseerd zijn op de gehele WPV-N: gezien het feit dat de grotere effecten op itemniveau gevonden werden voor weinig getoonde items, mag verwacht worden dat de effecten op schaalniveau bij de APV nog kleiner zijn.2
Om de behaalde resultaten te verifiëren is ook via logistische regressie DIF en DTF onderzocht. Hieruit bleek dat er weinig tot geen sprake was van DIF of DTF. Uit de analyses bleek wel dat er verschillen in gemiddelde scores waren, waarbij de Selectiegroep over het algemeen hoger scoorde dan de Adviesgroep. Dit is een bekend gegeven uit de selectie- en assessment literatuur
(Birkeland et al., 2006). De resultaten van beide methoden samen nemend is geconcludeerd dat de items niet anders functioneren onder de verschillende testsituaties; daarom is besloten de Selectiegroep simpelweg te scoren met de itemparameters gekalibreerd op de Adviesgroep, maar wel een Selectienormgroep te hanteren om voor vertekeningen in gemiddelde scores te corrigeren.
3.3. Ontwikkeling Selectienormgroep
Net als bij de Adviesnormgroep is er door middel van het trekken van een steekproef uit de ongewogen groep een representatieve normgroep wat betreft leeftijd, opleiding en geslacht gecreëerd. Bij een N van 1000 was de balans tussen een zo groot mogelijke steekproef en een zo klein mogelijke afwijking van de CBS verdelingen wat betreft geslacht, leeftijd en opleiding optimaal. Na weging was er geen verschil in verdeling wat betreft geslacht tussen de gewogen steekproef en het CBS (χ2(1) = .06, p = .80). Er waren slechts kleine tot gemiddelde verschillen voor leeftijd (χ2(4) = 18.25, p < .001, Cramer’s V = .07) en opleiding (χ2(2) = 33.79, p < .001, Cramer’s V = .13). De verdeling wat betreft geslacht, leeftijd en opleidingsniveau in de gewogen Selectienormgroep is weergegeven in Tabel 1.20.
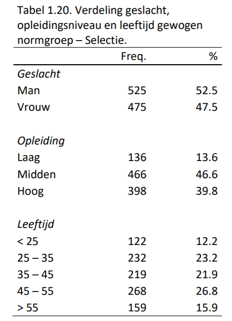
Net als bij de Adviesnormgroep is bij de Selectienormgroep de eerste versie van de APV gesimuleerd (zie pagina 25 voor de specificaties van de vragenlijst). Nadat iedere persoon in de normgroep de APV had doorlopen zijn de theta-scores genormeerd met de continue fit-methode (zie Van der Woud, 2007). De kenmerken van de ruwe scores en de stenscores (die weergegeven in de rapportage van de APV) zijn weergegeven in Tabel 1.21.
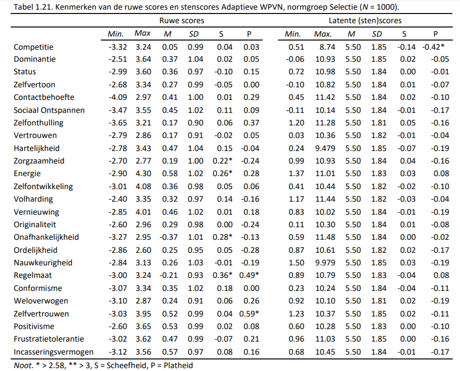
Net als bij de Adviesnormgroep is bij de Selectienormgroep de eerste versie van de APV gesimuleerd (zie pagina 25 voor de specificaties van de vragenlijst). Nadat iedere persoon in de normgroep de APV had doorlopen zijn de theta-scores genormeerd met de continue fit-methode (zie Van der Woud, 2007). De kenmerken van de ruwe scores en de stenscores (die weergegeven in de rapportage van de APV) zijn weergegeven in Tabel 1.21.
Ook zijn bij de Selectienormgroep de betrouwbaarheden berekend bij de adaptieve versie, de volledige versie gescoord via MIRT en de klassiek gescoorde WPV-N. Deze zijn weergegeven in Tabel 1.23.
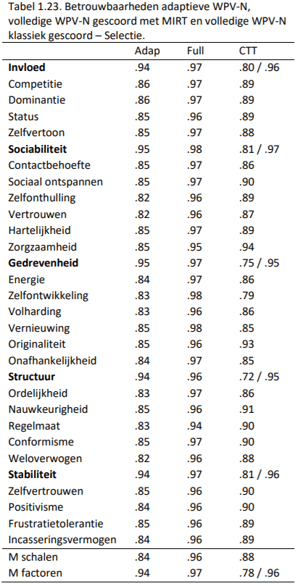
De betrouwbaarheden van de schalen zijn iets lager dan bij de Adviesgroep, maar nog steeds hoog. Voor de factoren geldt dat de betrouwbaarheden zeer hoog zijn. Gemiddeld zijn er 95 items (SD = 10.2, Min. = 64, Max. = 148) nodig om tot deze betrouwbare schattingen te komen; dit zijn gemiddeld slechts 3 items meer dan bij Advies. Dit is een gemiddelde reductie van 66%. Qua afnametijd betekent dit dat de APV ook in selectiesituaties ongeveer 10 tot 25 minuten zal duren, vergeleken met 30 tot 40 minuten bij de WPV-N.
4. Handleiding voor testgebruikers
De APV is gebaseerd op de WPV. Inzet van het instrument en de rapportage zijn daarom vergelijkbaar. Om deze reden verwijzen we u naar de handleiding van de WPV.

